TRANSFORMACJA LORENTZA - Weźmy pod uwagę dwa układy inercjalne S i S`, których osie x i x` są do siebie równoległe, a początki O i O` pokrywają się w układzie S ze stałą prędkością v , zwróconą zgodnie ze zwrotem osi x. Gdy pewne zdarzenie zaobserwowane w układzie S ma współrzędne x,y,z,t, to odpowiednie jego współrzędne w układzie S` wynoszą x`,y`,z` ,t`. Układy odniesienia wybieramy w taki sposób, żeby zawsze y` = y i z` = z i tymi współrzędnymi nie będziemy się zajmować. Mamy więc w każdym układzie jedną współrzędną przestrzenną (x lub x`) i jedna współrzędną czasową (t lub t`).

Równanie czoła fali kulistej :

x²+y²+z²=c²t²

x'²+y'²+z'²=c²t'²

stosuję podstawienia

x' = x - v t

y' = y

z' = z

t' = t + f x

c't' - promień kuli

podstawiam wartości i rozwiązuję układ równań , przy czym 2c²f + 2v = 0 ⇒

f = -(v / c²) , współczynnik

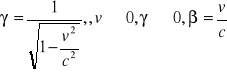
x' = γ( x - v t) x = γ( x' +vt')

y' = y y = y'

z' = z z = z'

t' = γ( t - (v/c²)x) t = γ( t'- (v/c²)x')

SKRÓCENIE DŁUGOŚCI

Mamy dwa układy s i s', mierzymy długość w obydwu układach : l'- długość zmierzona przez obserwatora w ruchomego ,l- opisuje długość jaką zaobserwuje obserwator nie będący w ruchu ,gdzie :

l₀ = x₂ - x₁ , l' = x₂' - x₁'

l₀=x² - x¹= γ(x₂'+vt')-γ(x₁'+vt') =γ(x₂'-x₁')

l'=l₀/γ =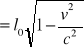
ciało obserwowane w ruchu jest „krótsze” od ciała w spoczynku

MASA RELATYWISTYCZNA, ENERGIA W TEORII WZGLĘDNOŚCI - m. = γm₀ - masa ciała kiedy się porusza, nie jest równa masie ciała kiedy jest w spoczynku. Zmiana masy jest wynikiem płynięcia czasu w dwóch układach.
Energia relatywistyczna: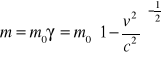

V - małym:

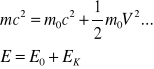
m - całkowita masa jest cał. energią zawartą w masie, m₀c² - energia spoczynkowa, 1/2m₀V² - prędkość ruchu, E - energia całkowita, E₀ - energia spoczynkowa,

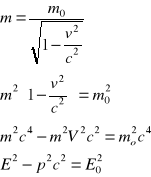
dla E₀ = 0, E = p ⋅ c

p = mV = E / c² V = (p / c) ⋅ V,

V⇒ c - wartość prędkości jest równa wartości c.

OSCYLATOR HARMONICZNY - Aby zaistniał ruch potrzebna jest siła :

F = -kx (x-wychylenie, k-sprężystość ukł)

m*a = -kx , to a + k/m x =0 , a -przyspie.

Możemy również zapisać :

x(t) = Asin (ωt + f₀)

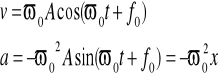
a stąd:

A - amplituda drgań

ωt +f₀ - faza drgań

ω₀ - prędkość kołowa , pulsacja , częstość

OSCYLATOR TŁUMIONY - W rzeczywistym oscylatorze w wyniku działania tarcia amplituda drgań maleje stopniowo aż do zera.

F = ma lub -kx - b(dx/dt) =m(d²x/dt²)

-b(dx/dt) - siła tłumiąca, jeżeli b jest mała:

lne^βT = βT - log. deklement tłumienia

β = r/2m - współczynnik tłumienia

PRAWO KOULOMBA - Dwa nieruchome ładunki elektryczne q oraz Q oddziałują na siebie siłą daną wzorem:

Lub w zapisie wektorowym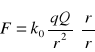

Stała k_o zależy tylko od układu jednostek. W układzie SI: k₀ = 1 / (4πε_oε). Stała: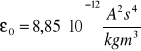

Kulomb jest ładunkiem, który na drugi taki sam ładunek działa z odległości 1 [m.] siłą równą 9 ⋅ 10⁹ [N]. Kulomb jest jednostką pochodną ampera. Wartość jednego kulomba ma ładunek elektryczny, przepływający w czasie jednej sekundy przez przewodnik, w którym płynie prąd o natężeniu jednego ampera. Przyjmuje się że siła jest dodatnia dla ładunków równoimiennych, a ujemna dla różnoimiennych. Zakres stosowalności prawa Kulomba rozciąga się od 10^-15 [m.]. do kilkudziesięciu lat świetlnych.

POLE MAGNETYCZNE I JEGO WZGLĘDNOŚĆ - Dwa równoległe przewodniki, przez które płynie prąd, przyciągają się lub odpychają się. Obserwując zamiast dwóch przewodników strumień swobodnych elektronów w pobliżu przewodnika z prądem, również stwierdzimy odchylenie biegu elektronów po włączeniu prądu. Można więc przyjąć, że w przestrzeni otaczającej przewodnik z prądem znajduje się pole magnetyczne. Pole to opisujemy za pomocą wektora indukcji magnetycznej
, zdefiniowanego przez siłę elektrodynamiczną działającą na poruszający się ładunek:

w próżni

Pole magnetyczne jest polem bezżródłowym , jest polem wirowym. Nie mam szans na otrzymanie pojedynczego bieguna N lub S .

Cyrkulacja

RÓWNANIE MAXWELLA - Maxwell traktował przestrzeń jako ośrodek materialny - eter. Jeśli w przestrzeni nie ma żadnej dotykalnej materii ,prąd przesunięcia płynie w jakimś ośrodku.

Postać różniczkowa: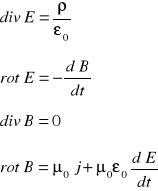

μ₀ i ε₀ - stałe które charakteryzują własności próżni w sensie magnetycznym ( gdy nie ma materii)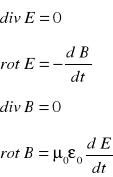

Są to cztery sprzężone równania różniczkowe cząstkowe .Stosują się one do każdego punktu przestrzeni pola elektromagnetycznego. W próżni gęstość ładunku ρ oraz prądu I równa się zero.

Maxwell jako pierwszy zasugerował, że światło jest falą elektromagnetyczną o określonym zakresie częstotliwości.

PRAWO OHMA - Przepływ prądu w przewodniku jest wywołany działaniem pola elektrycznego na nośniki ładunku znajdujące się wewnątrz przewodnika. Jeżeli do końców przewodnika doprowadzimy napięcie U to wytworzone w ten sposób pole elektryczne spowoduje przepływ prądu o natężeniu I.

Iloraz R=U/I nazywamy oporem elektrycznym [

Stosunek napięcia między dwoma punktami przewodnika do natężenia przepływającego przezeń prądu jest wielkością stałą i nie zależy ani od napięcia ani od natężenia prądu. Twierdzenie to nosi nazwę prawa Ohma.

Z powyższego wzoru można napisać, że I=U/R czyli natężenie prądu jest wprost proporcjonalne do przyłożonego napięcia. Prawo Ohma jest ściśle słuszne tylko gdy temperatura = const.

Prawo Ohma stosuje się do wszystkich ciał jednorodnych i izotropowych przy niewielkich napięciach i natężeniach prądu.

Opór danego przewodnika zależy od jego wymiarów i jest on wprost proporcjonalny do długości L oraz odwrotnie proporcjonalny do przekroju poprzecznego S przewodnika.

R= ρL/S

Współczynnik ρ nosi nazwę oporu właściwego. Ze względu na opór właściwy ciała dzieli się umownie na grupy:
- metale będące b. dobrymi przewodnikami
- półprzewodniki
- elektrolity
- izolatory
Odwrotność oporu nazywa się przewodnością, a odwrotność oporu właściwego - przewodnością właściwą. Zatem:

δ=1/ ρ
Ustalimy obecnie związek między natężeniem pola elektrycznego w przewodniku a gęstością prądu. W tym celu zauważamy, że jeżeli przewodnik ma długość L, to przy napięciu U natężenie pola E=U/I
Przy założeniu, że prąd jest rozłożony równomiernie w całym przekroju przewodnika, gęstość prądu w tym przewodniku wynosi:
j=L/S
j=U/RS=EL/RS=E/ρ=δE

(pytanie 46:)
Wzór powyższy j=δE wyrażający proporcjonalność prądu do natężenia pola elektrycznego jest inną postacią prawa Ohma. Nazywamy go różniczkowym prawem Ohma. Wyraża ono lokalne własności przewodnika. Związek zapisujemy często w postaci wektorowej.

NATĘŻENIE PRĄDU ELEKTRYCZNEGO - Natężenie prądu elektrycznego I płynącego przez przewodnik jest wprost proporcjonalne do napięcia U przyłożonego między końcami przewodnika.

I ~ U

Dla danego odcinka obwodu stosunek napięcia mierzonego na jego końcach do natężenia na jego końcach do natężenia prądu przez niego przepływającego ma stałą wartość i nazywa się oporem elektrycznym R.

U

R = --- = const

I

Jednostką oporu elektrycznego jest 1 om (1Ω).

1Ω jest to opór takiego przewodnika, w którym pod napięciem 1V płynie prąd o natężeniu 1A.

INERCJALNE UKŁADY ODNIESIENIA - Układ odniesienia , w którym obowiązują zasady dynamiki Newtona, nazywamy układem inercjalnym.

Według I zasady dynamiki Newtona układ inercjalny wyróżnia się tym, że ciało nie poddane działaniu sił spoczywa lub porusza się jednostajni prostoliniowo względem tego układu. Doświadczenia wykazują, że układ odniesienia związany z Ziemią jest w bardzo dobrym przybliżeniu układem inercjalnym. Jednak ruch obrotowy Ziemi wokół własnej osi wpływa w niewielkim stopniu na przebieg zjawisk mechanicznych (dowód wahadło puszczone w ruch poziomy). Dokładniejszym układem inercjalnym jest układ związany z gwiazdami.

Każdy układ poruszający się względem układu inercjalnego ruchem jednostajnym i prostoliniowym jest też układem inercjalnym.

NIEINERCJALNE UKŁADY ODNIESIENIA - Przypuśćmy, że obserwujemy ruch punktu materialnego P w pewnym inercjalnym układzie odniesienia, który oznaczmy przez O. Rozważany punkt znajduje się pod działaniem innych sił materialnych, więc porusza się ruchem jednostajnym (F=m*a) Weżmy teraz pod uwagę drugi układ odniesienia O' , poruszający się względem układu O w kierunkuosi x ruchem dowolnym.

Na podstawie rysunku widzimy , że x'(t) = x(t) - x_o(t), po dwukrotnym zróżniczkowaniu otrzymujemy:

a' = a - a_o

Z powyższego związku widać, że przyspieszenie w układzie O' , nie jest równe przyspieszeniu w układzie O. Równość taka zachodzi tylko dla a_o=0 , a więc gdy przyspieszenie układu O' względem O jest równe zeru, gdy układ O' jest układem inercjalnym. Jeżeli zaś
to układ O' nazywamy układem nieinercjalnym, a przyspieszenie a_o - przyspieszeniem unoszenia.

W układzie O' nie obowiązuje I zasada dynamiki: punkt materialny nie spoczywa , lecz porusz sie z przyspieszeniem a' = - a_o. Układ ten nie jest układem inercjalnym i nie działa w nim także II zasada dynamiki: iloczyn masy i przyspieszenia nie jest równy sile działającej na masę, lecz równy jest sile mnius wyrażenie m*a_o.

Zdefiniujemy teraz siłę bezwładności F_b jako iloczyn masy i przyspieszenia unoszenia ze znakiem minus:

F_b = - m*a_o

Siłę bezwładności nazywa się siłą pozorną, gdyż jej istnienie zależy od wyboru nieinercjalnego układu odniesienia.

W obracającym się układzie odniesienia występuje siła bezwładności, zwana odśrodkową siłą bezwładności.

F_od = m*ω²*r

SIŁA CORIOLISA - Jeżeli ciało porusza się względem wirującego układu odniesienia(rys a), to — oprócz odśrodkowej siły bezwładności — pojawia się jeszcze jedna siła, zwana silą Coriolisa lub silą bezwładności Coriolisa. W wirującym układzie odniesienia cząstka zachowuje się tak, jakby — oprócz skierowanej do środka okręgu siły F — działały na nią jeszcze dwie siły: F_bo = mω² R i Fc, której wartość wynosi 2mv'ω. Łatwo jest przekonać się, że siłę Fc można przed­stawić w postaci Fc = 2m [v'<a].

Siła ta jest właśnie siłą bezwładności Coriolisa. Jeżeli v' = O, to siła Coriolisa jest równa zeru. Natomiast siła f|», nie zależy od v' — działa ona zarówno na spoczywające, jak i poruszające się cząstki. Dla przypadku przedstawionego na rysunku b mamy

A następnie

ZASADA ZACHOWANIA MOMENTU PĘDU - Stosunek zmiany całkowitego momentu pędu układu punktów materialnych względem punktu związanego z inercjalnym układem odniesienia (albo względem środka masy) do czasu, w którym ta zmiana nastąpiła jest równy sumie momentów sił zewnętrznych działających na ten układ, tzn: ၴ_zew=dL/dt. Przypuśćmy teraz, że suma momentów sił zewnętrznych ၴ_zew =0; znaczy to, że dL/dt=0, zatem L jest wektorem stałym. Jeśli wypadkowy moment sił zewnętrznych działających na układ wynosi zero. Całkowity moment pędu pozostaje stały. Dla układu n punktów materialnych całkowity moment pędu względem pewnego punktu wynosi L=l₁+l₂+...l_n. Jeśli wypadkowy moment sił zewnętrznych działających na układ wynosi zero, to L=const=L₀, gdzie L₀ jest stałym wektorem całkowitego momentu pędu. Momenty pędu poszczególnych punktów materialnych mogą się zmieniać, lecz ich suma wektorowa L₀ pozostaje stała gdyż wypadkowy moment sił zewnętrznych równa się zeru.

Przykład.

Jeśli układem punktów materialnych jest ciało sztywne obracające się wokół pewnej osi (np. osi z), która jest nieruchoma w inercjalnym układzie odniesienia, to możemy zapisać że L_Z=Iთၷ, gdzie L_Z jest składową momentu pędu wzdłuż osi obrotu, a I jest momentem bezwładności układu względem tej samej osi. Gdy skoczek odbija się od trampoliny z wyciągniętymi nogami i rękoma posiada pewną początkową prędkość kątową. Ponieważ w powietrzu nie występują momenty sił zewnętrznych, jego moment pędu L=I*omega jest stały. Gdy skoczek podkurczy nogi i ręce, zmaleje, ale odpowiednio wzrośnie ၷ. Moment pędu nie ulegnie zmianie L=Iთၷ=I₀თၷ₀=const.

TWIERDZENIE GAUSSA DLA ELEKTROSTATYKI - całkowity strumień Φ wektora indukcji elektrycznej D przez powierzchnię zamkniętą S o dowolnym kształcie jest wprost proporcjonalny do sumy algebraicznej swobodnych ład. Elektrycznych zawartych wewnątrz tej powierzchni i nie zależy od ładunków rozmieszczonych na zewnątrz niej.

Φ = ∑_k=1ⁿ q_k gdzie q₁, q₂, .. to ładunki zawarte wewnątrz powierzchni.

Uwzględniając wyrażenie na całkowity strumień indukcji elektrycznej, twierdzenie to można zapisać:

Φ = ƒƒ_s D_n ds = Q / (_{ρ } _e)

gdzie: Q - ładunek całkowity wewnątrz zamkniętej powierzchni S.

Dla pola magnetycznego: strumień wektora indukcji magnetycznej przez dowolną powierzchnię zamkniętą jest równy zeru

Φ = ƒƒ_s B ds = 0

ładunki leżące na zwenątrz nie mają wpływu na wartość E jeżeli rozkład ładunków jest odp. symetryczny, iż prez odpowiedni dobór powierzchni Gaussa da się wyznaczyć całkę Φ_E=ƒEdS. Prawo gaussa może być stosowane do obliczania ładunku znajdującego się wewnątrz powierzchni.

Jak wynika prawo Columba

ε₀∫Eds=q

ε₀E∫ds=q

ε₀E(4πr²)=q

E=1/4πr²ε₀*q/r², ale E=F/q₀ --> F=1/1/4πr²ε₀*qq₀/r² - prawo Coulomba

INDUKCJA ELEKTROMAGNETYCZNA - zjawisko powstawania w obwodzie elektrycznym siły elektromagnetycznej indukcji _i w wyniku zmian w czasie strumienia magnetycznego obejmowanego przez ten obwód (prawo Faraday'a)

_{δ } ƒ_ _ δ   (δΦ_  (δ   ƒƒƒ_σ ∂  ∂

Gdy obwód jest zamknięty, zaczyna w nim płynąć prąd elektryczny zwany prądem indukowanym. W praktyce można uzyskać prąd indukowany w następujących przypadkach:

1. gdy obwód zamknięty porusza się w polu magnetycznym magnesu w ten sposób, że przecina linie sił pola magnetycznego;

2. gdy obwód jest nieruchomy, a porusza się magnes (zależy to więc jedynie od ruchu względnego między obwodem, a magnesem);

3. gdy zamiast magnesu zostanie użyta cewka z prądem, która wytwarza pole magnetyczne;

4. gdy w poprzednim przypadku obwody pozostają nieruchome, ale w cewce zmienia się natężenie prądu;

Kierunek powstającego prądu indukowanego określony jest przez regułę Lenza (kierunek prądu indukowanego jest taki, że wytworzone przez niego pole magnetyczne przeciwstawia się przyczynie, która go wywołała).

Samoindukcja - szczególny przypadek indukcji elektromagnetycznej, zjawisko powstawania siły elektromotorycznej (SEM) w obwodzie zamkniętym w wyniku zmian strumienia indukcji magnetycznej wytwarzanego przez zmienny prąd elektryczny płynący przez ten obwód. Wielkość SEM wynosi

_σ      

, gdzie    - szybkość zmian natężenia prądu w obwodzie

L - współczynnik samoindukcji

MOMENT BEZWŁADNOŚCI BRYŁY SZTYWNEJ - ciało sztywne - układ punktów materialnych, które zajmują zawsze te same położenie względme siebie.

Weźmy pod uwagę ciało sztywne obracające się z prędkością kątową ω dokoła osi, które jest nieruchome w wybranym układzie inercjalnym. Każdy punkt tego ciała ma energię kinetyczną. Punkt materialny o masie m i odległości r od osie obrotu i ma prędkość liniową v=ωr. Jegeo energia kinetyczna wynosi zatem mv²/2=mr²ω²/2 całkowita energia kinetyczna ciała jest sumą energii kinetycznych wszystkich jego punktów. Dla ciała sztywnego ω jest stałe dla wszystkich punktów materialnych. Promień r może być różny dla róznych punktów. Stąd całkowita energia kinetyczna K obracającego sie ciała wyraża się jako K=1/2(m₁r₁²+...)ω²=1/2(Σm_ir_i²) ω². Czynnik (Σm_ir_i²) hest sumą iloczynów mas cząstek przez kwadraty ich odległości od osi obrotu. Oznaczając tę wielkość przez I nazywamy momentem bezwładności ciała względem wybranej osi.

ciągły rozkład masy - dla ciała sztywnego, które nie składa się oddzielnym mas punktowych, lecz ma ciągły rozkład masy, wyrażenie określające moment bezwładności jest bardziej złożone. Proces sumowania we wzorze I=(Σm_ir_i²) zastępujemy procesem całkowania. rozważmy ciało podzielone na nieskończenie małe elementy o masach dm. Niech r oznacza odległość każdego elementu od osi obrotu. Wówczas moment bezwładności otrzymujemy z wyrażenia I=∫r²dm, gdzie całkowanie odbywa się po całej objętości ciała.

PRAWO AMPERA - krążenie wektora natężenia pola magnetycznego po dowolnej krzywej zamkniętej jest równe algebraicznej sumie natężeń prądów przepływających przez powierzchnię rozpiętą na tej krzywej.

_ _ _  _ _

Prawo ampera - prawo przedstawiające zależność wartości cyrkulacji (całki okrężnej) wektora natężenia pola magnetycznego H od wartości natężeń stałych prądów elektrycznych płynących przez powierzchnię objętą cyrkulacją; cyrkulacja wektora natężenia pola magnetycznego, wytworzonego przez stały prąd elektryczny, wzdłuż linii zamkniętej L obejmującej prąd jest równa sumie algebraicznej natężeń I_k prądów obejmowanych przez tę linię

ƒ_L Hdl = ∑_k=1ⁿ I_k

Względną wartość indukcji B dla różnych odległości n i przy róznych natężeniach i możemy wyznaczyć, dowodząc doświadczalnie, że B=i/r. Proporcjonalność tę możemy zamienić na równość wprowadzając stałą wówczas μ₀/2π, gdzie μ₀ - przenikalność magnetyczna. wówczas B=μ₀i/2πr albo 2Bπr=μ₀i. Lews strona ostatniego równania jest równe ∫Bdl po obwodzie koła o promieniu r, w które środku umieszczono drut. We wszystkich punktach tego koła B ma tę samą (stałą) wartość bezwzględną B, a dl -styczne do drogi całkowania ma ten sam kierunek co B. Wobec tego ∫Bdl=B∫dl=2Bπr, gdzie ∫dl jest obwodem koła. A więc w tym szczególnym przypadku możemy zapisać związek pomiędzy polem magnetycznym i prądem jako ∫Bdl=μ₀i - co stanowi prawo Ampera.

Ampera reguła (reguła pływaka) - reguła określająca zależność między kierunkiem pola magnetycznego, a kierunkiem prądu elektrycznego wytwarzającego to pole: człowiek płynący wzdłuż przewodnika w kierunku prądu elektrycznego i zwrócony twarzą do igły magnetycznej umieszczonej pod przewodnikiem widzi północny biegun tej igły odchylony na lewo.

PRAWO BIOTA-SAVARTA - Prawo Ampera można stosować do znajdowania pola magnetycznego tylko wtedy, gdy rozkład prądów jest na tyle symetryczny, że pozwala na łatwe obliczenie całki krzywoliniowej ∫Bdl. Podobnie prawo Gaussa stosuje się w elektrostatyce do znajdowania pół elektrostatycznych wówczas tylko, jesli rozkład ładunku ma na tyle wysoką symetrię, że łatwo jest policzyć całką powierzchniową ∫Eds

Chcąc znaleźć idnukcję dB pola magnetycznego wytworzonego przez element prądu w pnkcie P. Zgodnie z prawem Biota-Savarta dB=μ₀i/4π * dl sinθ/r², gdzie r jest promieniem wodzacym, poprowadzonym od elementu prądu do punktu P, a θ kąt zawarty między r i dl. Zapisując to w postaci wektorowej otrzymamy dB==μ₀i/4π * (dl x r)/r³ _­gdzie

Prawo określające wielkość i kierunek wektora indukcji magnetycznej w dowolnym punkcie pola magnetycznego wytwarzanego przez prąd elektryczny, pozwalające znaleźć rozkład pola magnetycznego wytworzonego przez dowolny układ przewodników z prądem. Zgodnie z tym prawem, odcinek przewodnika , wzdłuż którego płynie prąd o natężeniu I, wytwarza w danym punkcie M przestrzeni, pole magnetyczne o indukcji magnetycznej

dB = [(μ₀ * μ_r * I)/4π]*[(dl * sin α)/r²]

B = [(μ₀ * μ_r * I)/4π]*ƒ[(dl * r)/r³]

φHdl = I

H = [(μ_r * I)/4π]*ƒ[(dl * r)/r³]

11)Równanie ruchu dla bryły obrotowej

Gdy na bryłę działa niezrównoważony moment siły M , wtedy nadaje on tej bryle przyspieszenie kątowe , którego wartość jest proporcjonalna do wartości momentu siły
, gdzie I- moment bezwładności bryły.
,

PRAWO POWSZECHNEGO CIĄŻENIA - Wszystkie ciała obdarzone masą przyciągają się wzajemnie siłami grawitacji. Wartość siły wzajemnego przyciągania się dwu ciał jest wprost proporcjonalna do iloczynu ich mas i odwrotnie proporcjonalna do kwadratu odległości między ich środkami. Wektor siły grawitacji leży na prostej przechodzącej przez środki obu mas.

RUCH - zmiana położenia obiektu materialnego względem pewnego punktu odniesienia; opis ruchu abstrahujący od działających sił stanowi przedmiot kinematyki, dynamika bada związek ruchu z działającymi siłami.

R. JEDNOSTAJNY - ruch, w którym stała jest bezwzględna wartość przyspieszenia, czyli przyspieszenie styczne (a_t) i dośrodkowe (a_n) jest równe zeru; wzory: s=υt υ=const a_t=a_n=0

R. JEDNOSTAJNIE PRZYSPIESZONY - ruch, w którym przyspieszenie styczne ma stałą wartość; wzory:

gdzie υ(t)-pr. jako funkcja czasu, υ₀ -pr. początkowa, a_t -przyspieszenie styczne a_t≠0=const a_n=0 υ - zmienne; ruch, w którym a_t<0 nazywamy ruchem jednostajnie opóźnionym

MOMENT PĘDU (KRĘTU) - Momentem pędu „L” punktu materialnego o masie „m” i wektorze wodzącym „r” od tego punktu definiujemy wzorem L = r x mv (co można zapisać
)

Moment pędu bryły jest sumą momentów pędu wszystkich jej punktów, czyli
albo L=IL_o

Moment pędu bryły równa się iloczynowi jej prędkości kątowej „ω” i momentu bezwładności „I”.

Posługując się pojęciem momentu pędu można II zasadą dynamiki ruchu obrotowego można wyrazić następująco : Pochodna momentu pędu „L” bryły względem czasu „t” jest równa momentowi siły „M” działającej na tę bryłę.

Mamy :

P.S. II zasada dynamiki:

Moment siły działającej na bryłę jest równy iloczynowi momentu bezwładności „I” tej bryły i jej przyspieszenia kątowego „α”. M. = I_α

Natomiast: Moment bezwładności I bryły względem dowolnej osi jest równy sumie momentu bezwładności „I₀” względem osi równoległej przechodzącej przez środek masy bryły oraz iloczyn masy tej bryły i kwadratu odległości obu osi, czyli I=I₀+mα²

FALE ELEKTROMAGNETYCZNE I ICH WŁASNOŚCI, INDUKCJA ELEKTROMAGNETYCZNA - Obwodem LC nazywamy obwód zawierający kondensator o pojemności C i cewkę o indukcyjności L, o oporze elektrycznym równym zero. W obwodzie LC można pobudzić drgania elektryczne, które wykazują ścisłą analogię do drgań mechanicznych.

W rzeczywistości każdu\y obwód posiada mniejszy lub większy opór R. Jego obecność powoduje w każdym cyklu wydzielanie się w obwodzie pewnej ilości ciepła Joule'a, energia obwodu maleje i drgania zanikają. Otrzymujemy w ten sposób drgania swobodne tłumione.

Współczynnik tłumienia =R/2L

W obwodzie zawierającym opór (RLC) można uzyskać drgania niezanikające, nazywane drganiami wymuszonymi, jeżeli w obwód włączymy zmienną SEM (indukcyjną siłę elektromotoryczną) Drgania wymuszone można także wywołać bez włączania żródła SEM. Jeżeli do obwodu drgającego zbliżymy drugi obwód, to siła magnetyczna cewki obwodu 1 będzie indukowała SEM w cewce obwodu 2 i w obwodzie 2 powstaną drgania

Są obwody o ...

Indukcja elektromagnetyczna (prawo indukcji Faradaya)

Zjawisko indukcji elektromagnetycznej polega na powstawaniu prądów elektrycznych wskutek zmian pola magnetycznego. Aby matematycznie ująć zjawisko indukcji wprowadzamy pojęcie strumienia indukcji magnetycznej _B

_B =_S BdS

tzn. całka powierzchniowa wektora B po zorientowanej powierzchni S

Jeżeli w jednym obwodzie zmienia się natężenie prądu, to zgodnie z prawem indukcji Faradaya w drugim obwodzie znajdującym się w pobliżu jest indukowana SEM. Zjawisko to nazywane jest indukcją wzajemną. W przypadku pojedynczego obwodu występuje tzw. Zjawisko indukcji własnej.

PRZYSPIESZENIE - Podstawowa wektorowa wielkość fiz. charakteryzująca ruch; przyspieszenie opisuje szybkość zmian wektora prędkości ciała: przyspieszenie liniowe
— wektora prędkości liniowej
, przyspieszenie kątowe
— wektora prędkości kątowej. Przyspieszenie liniowe jest równe pochodnej prędkości liniowej względem czasu

a przyspieszenie kątowe — takiej samej pochodnej prędkości kątowej:

(często wystarczy posługiwać się wartościami średnimi

_średnie = Δ
 /Δt,
_średnie = Δ
 /Δt

Rzuty przyspieszenia liniowego na styczną i normalną do toru noszą odpowiednio nazwy przyspieszenia stycznego
_t (charakteryzuje zmianę wartości prędkości) i przyspieszenia normalnego
_r (dośrodkowego; charakteryzuje zmianę kierunku prędkości). Jednostkami przyspieszenia są: przyspieszenia liniowego — m/s², przyspieszenia kątowego — rad/s², stopień/s² i in.

PRĘDKOŚĆ - Podstawowa, wektorowa wielkość fiz. charakteryzująca ruch. Przy opisie ruchu postępowego wprowadza się pojęcie prędkości liniowej
, prędkość liniowa jest równa pochodnej wektora położenia
względem czasu t:

a jej wartość v — pochodnej drogi s względem czasu:

w ruchu jednostajnym v równa się stosunkowi drogi s do czasu, w którym ta droga została przebyta: v = s/t; prędkość liniowa jest styczna do toru; jednostki prędkości liniowej: m/s, km/h. Ruch obrotowy charakteryzuje prędkość kątowa
; wektor prędkości kątowej jest skierowany wzdłuż osi obrotu i zwrócony w stronę, z której obrót ciała widać jako przeciwny do ruchu wskazówek zegara; wartość prędkości kątowej jest równa pochodnej kąta obrotu względem czasu t:

jednostki prędkości kątowej: rad/s, stop/s i in. Między prędkością liniową punktu ciała a jego prędkością kątową w ruchu obrotowym zachodzi związek

— wektor położenia punktu

PĘD -
, jedna z podstawowych wielkości fiz. charakteryzujących ruch układu; pęd punktu materialnego o masie m i prędkości
równy jest

pęd układu mech. jest sumą wektorową pędów poszczególnych punktów układu lub iloczynem całkowitej masy M układu i prędkości
jego środka masy.

ZASADA ZACHOWANIA PĘDU - Pędu odosobnionego (izolowanego) układu mech., tj. nie poddanego oddziaływaniom zewn., pozostaje wielkością stałą. Siły wewn. nie mogą zmieniać całkowitego pędu układu, choć pędy poszczególnych ciał mogą ulegać zmianie (zasada zachowania pędu tłumaczy m.in. zjawisko odrzutu przy wystrzale).

Zmiana pędu może zachodzić jedynie w wyniku oddziaływań zewn.; zmianę tę wyraża zależność

gdzie
— wypadkowa sił zewn., t — czas jej działania. Pęd mają wszystkie formy materii, także pole grawitacyjne i eletromagnet.

NEWTONA ZASADY DYNAMIKI - 3 podstawowe prawa dynamiki. I zasada dynamiki Newtona, zw. też zasadą bezwładności : jeśli na ciało nie działają żadne siły lub jeśli działające siły wzajemnie się równoważą, to istnieje układ odniesienia, w którym ciało spoczywa lub porusza się ruchem jednostajnie prostoliniowym;

II zasada dynamiki Newtona: zmiana pędu ciała jest proporcjonalna do przyłożonej siły

w mechanice nierelatywistycznej równanie to sprowadza się do postaci

m — masa ciała,
— jego prędkość,
— przyspieszenie,
— siła działająca, t — czas); dla ruchu obrotowego II zasada dynamiki przyjmuje postać:

gdzie I — moment bezwładności ciała,
— przyspieszenie kątowe, M — moment siły

III zasada dynamiki Newtona, zw. prawem akcji i reakcji (słuszna tylko w mechanice nierelatywistycznej): każdemu działaniu towarzyszy równe mu, skierowane przeciwnie — przeciwdziałanie. Zasady dynamiki Newtona są spełnione w inercjalnych układach odniesienia; w układach nieinercjalnych są słuszne dopiero po uwzględnieniu — oprócz sił rzeczywistych — fikcyjnych → sił bezwładności

PRACA - Skalarna wielkość fiz. określająca wartość energii wydatkowanej na przemieszczenie ciała materialnego z jednego położenia do drugiego. Praca wykonywana przez siłę
działającą na ciało przemieszczające się od punktu A do B jest równa

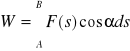
gdzie d
— wektorowy element drogi; jeśli
 = const, a ciało porusza się ruchem prostoliniowym, to

W = Fs cosα

gdzie α — kąt między kierunkiem siły i drogi.

Pracę wykonaną przez prąd elektr. określa prawo Joule'a-Lenza, które w ogólnym sformułowaniu ma postać

gdzie
— wektor gęstości prądu elektr.,
— wektor natężenia pola elektr., a całkowanie odbywa się po objętości przewodnika V i czasie t; dla prostszego przypadku stałego prądu elektr. W = U I t (U — napięcie, I — natężenie prądu elektr.). Jednostką pracy w układzie SI jest dżul.

Siłę potencjalną niezależną od czasu nazywa się siłą zachowawczą. Praca sił zachowawczych jest równa różnicy potencjałów sił w punktach odpowiadających początkowemu i końcowemu położeniu ciała i nie zależy od toru ruchu ciała.

ENERGIA KINETYCZNA - Część energii mech. układu fiz. (np. ciała sztywnego) zależna od prędkości jego punktów; w przypadku ciała sztywnego o masie m poruszającego się ruchem postępowym z prędkością v (znacznie mniejszą od prędkości światła) jego energia kinetyczna E _k = mv ²/2; energia kinetyczna ciała sztywnego obracającego się z prędkością kątową ω wokół pewnej osi E _k = Iω ²/2, gdzie I — moment bezwładności ciała względem tejże osi; wg

mechaniki relatywistycznej, gdzie m ₀ — masa spoczynkowa ciała, c — prędkość światła w próżni.

ENERGIA POTENCJALNA - Część energii mech. układu fiz. zależna od wzajemnego rozmieszczenia części układu (np. energia sprężysta) i od ich położenia w zewn. polu sił; miarą e.p. jest w danym położeniu jest praca, którą muszą wykonać siły działające na układ, aby przeprowadzić go z położenia, dla którego e.p. przyjmuje się umownie za równą zeru, do danego położenia; np. E_p ciała o masie m w polu grawitacyjnym Ziemi na wysokości h równa jest iloczynowi siły ciężkości mg (g — przyśpieszenie ziemskie) i h:

E_p = mgh.

ENERGII ZACHOWANIA ZASADA - Jedno z podstawowych praw fizyki: całkowita energia dowolnego izolowanego (tj. nie oddziałującego z otoczeniem) układu fiz. ma wartość stałą. Jeśli izolowany układ fiz. składa się z wielu oddziałujących wzajemnie podukładów, to energia podukładów może ulegać zmianie, ale całkowita energia wszystkich podukładów musi pozostać nie zmieniona. W procesach fiz. jedna forma energii może zmienić się w inną, np. energia mech. w energię prądu elektr., energia promieniowania elektromagnet. w energię kinet. ruchu cząstki, ale całkowita energia zawsze pozostaje stała.

Zgodnie ze szczególną teorią względności między całkowitą energią E i całkowitą masą układu m istnieje związek E = mc² , przy czym m zmienia się zależnie od prędkości układu (c — prędkość światła w próżni).

POLE GRAWITACYJNE - Rodzaj pola fiz.; stan przestrzeni fiz. odznaczający się tym, że na znajdujące się w tej przestrzeni ciała obdarzone masą działa określona siła (grawitacja).

KEPLERA PRAWA - Trzy prawa sformułowane (1609-19) przez J. Keplera na podstawie analizy obserwacji ruchu planet;

I prawo Keplera: orbita każdej planety jest elipsą, w której ognisku znajduje się Słońce

II prawo Keplera: promień wodzący planety zakreśla jednakowe pola w równych odstępach czasu (prawo pól);

III prawo Keplera: stosunek sześcianów wielkich półosi a orbit planet do kwadratów okresu T obiegu planet wokół Słońca (a³/T²) jest jednakowy dla wszystkich planet

BRYŁA SZTYWNA - Ciało sztywne, ciało, które nie ulega odkształceniu, niezależnie od wartości przyłożonych do niego sił.

MOMENT BEZWŁADNOŚCI - Mech. wielkość fiz. charakteryzująca bezwładność bryły sztywnej wykonującej ruch obrotowy; wartość momentu bezwładności zależy od rozmieszczenia masy bryły względem osi obrotu; moment bezwładności bryły względem osi z określa się wzorem:

,
,

gdzie ρ — gęstość materiału elementu bryły, będąca funkcją położenia punktu, V — objętość bryły, m_i — masa i-tego punktu materialnego bryły sztywnej, r_i (lub r) — jego odległość od osi z.

EULERA RÓWNANIA RUCHU OBROTOWEGO - Różniczkowe równania ruchu ciała sztywnego mającego jeden punkt nieruchomy:

,

,

,

gdzie ω_x, ω_y, ω_z — rzuty chwilowej prędkości kątowej ω na osie gł. wyprowadzone z punktu nieruchomego, I_x, I_y, I_z — momenty bezwładności ciała względem tych osi, M_x, M_y, M_z — momenty sił względem tych osi. Eulera równania ruchu obrotowego całkuje się po dodaniu do nich 3 równań kinematycznych opisujących wartości rzutów ω_x, ω_y , ω_z w zależności od kątów Eulera (φ, ψ,
):

,

,

.

WZGLĘDNOŚCI TEORIA - Za najważniejsze jej konsekwencje uznaje się: uzależnienie czasu przebiegu zjawisk fiz., masy cząstek i wielu innych wielkości od stanu ruchu układu, w którym te zjawiska są opisane; podanie związku E = mc² pomiędzy masą m i energią E ciała; eliminację z fizyki pojęcia eteru i nadanie polom fizycznym statusu samodzielnych obiektów fiz., charakteryzujących się masą, gęstościami pędu, energii, momentu pędu itp.; uznanie pewnych wielkości, uznawanych poprzednio za wielkości odrębne, za składowe jednej wielkości określonej w czasoprzestrzeni. Szczególna teoria względności stanowi podstawę konstrukcji współcz. akceleratorów cząstek, a kinematyka relatywistyczna jest potwierdzona tysiącami doświadczeń nad rozpraszaniem cząstek o wysokich energiach. Zasada względności Einsteina jest we współcz. fizyce przyjmowana jako jedno z podstawowych kryteriów metodol., które powinna spełniać każda teoria. W 1916 Einstein sformułował ogólną teorię względności. W teorii tej zjawisko powszechnego ciążenia jest spowodowane wystąpieniem krzywizny czasoprzestrzeni, która jest przestrzenią bardziej ogólną niż nie mająca krzywizny czasoprzestrzeń Minkowskiego. Właściwości geom. tej ogólnej czasoprzestrzeni zależą od ruchu i rozkładu materii oraz pól, i z kolei same określają ruch materii oraz mają wpływ na pola. Zależność ta jest określona przez równania Einsteina; rozwiązaniami tych równań są czasoprzestrzenie odpowiadające rozmaitym sytuacjom fiz., a jedną z nich, dla przypadku gdy nie ma materii i pól, jest czasoprzestrzeń Minkowskiego. W ogólnej teorii względności nie ma żadnych wyróżnionych układów odniesienia. Pojawiają się one jednak wtedy, gdy rozwiązania równań Einsteina mają pewnego rodzaju symetrie. Ogólna teoria względności przewiduje poprawki do ruchu ciał i światła w polu grawitacyjnym. Ogólna teoria umożliwia m.in. konstruowanie modeli kosmologicznych Wszechświata; jeden z takich modeli tłumaczy zaobserwowane zjawisko ucieczki odległych galaktyk rozszerzaniem się Wszechświata.

DYLATACJA CZASU - W teorii względności efekt polegający bądź na opóźnianiu się zegara będącego w ruchu w stosunku do zegara spoczywającego w pewnym inercjalnym układzie odniesienia (kinematyczna dylatacja czasu), bądź na opóźnianiu się zegara znajdującego się w silnym polu grawitacyjnym (grawitacyjna dylatacja czasu); oba te efekty zostały zaobserwowane: poruszające się z dużymi prędkościami nietrwałe cząstki elementarne (np. w promieniowaniu kosm.) żyją dłużej niż cząstki spoczywające, natomiast czułe zegary znajdujące się w górach spieszą się w stosunku do zegarów pozostawionych na poziomie morza (będących w silniejszym polu grawitacyjnym — bliżej środka Ziemi).

POLE ELEKTRYCZNE - 1) Jedna z postaci, w której przejawia się pole elektromagnet. działające na spoczywające ładunki elektr.; pole wytworzone przez nieruchome ładunki elektr. stanowi pole elektrostatyczne. Pole elektryczne w dowolnym punkcie jest scharakteryzowane przez wektor natężenia pola elektrycznego
zgodny co do kierunku i równy co do wartości sile, z jaką pole elektryczne działa na umieszczony w tym miejscu jednostkowy punktowy ładunek dodatni:
 = 
/q — ładunek elektr., na który dziala siła
); wewnątrz dielektryka pole elektryczne charakteryzuje wektor indukcji elektrycznej
; w niezbyt wielkich polach elektrycznych w dielektrykach jednorodnych
 = ε₀ ε _r
(ε₀ i ε_r odpowiednio przenikalność elektr. próżni i przenikalność względna danego ośr.); obliczenie natężenia pola elektrycznego w przypadku symetrycznie rozłożonych ładunków elektr. umożliwia prawo Gaussa; oddziaływanie dwóch ładunków elektr. za pośrednictwem pola elektrostat. opisuje prawo Coulomba; pole elektrostat. jest polem zachowawczym, tzn. praca przeniesienia ładunku wzdłuż drogi zamkniętej w tym polu jest równa zeru. Pole elektryczne powoduje przepływ ładunków elektr. w przewodniku, zaś w dielektryku jego polaryzację. Zmienne w czasie pola elektrycznego powodują powstanie pola magnet; jednostką SI natężenia pola elektrycznego jest wolt na metr (V/m).

POTENCJAŁ - Wielkość pomocnicza służąca do opisu wektorowego pola potencjalnego (zachowawczego, bezwirowego), np. pola grawitacyjnego, elektrostatycznego; potencjał w rozważanym punkcie pola P definiuje się jako całkę krzywoliniową z wektora pola (np. wektora natężenia pola elektrostat.
lub grawitacyjnego) obliczaną wzdłuż drogi L łączącej pewien punkt odniesienia O (zazwyczaj przyjmowany jako punkt położony w nieskończoności) z punktem P; w przypadku pól zachowawczych tak określany potencjał jest niezależny od kształtu drogi całkowania L łączącej punkty O i P i dlatego może służyć do jednoznacznego opisu pola; wartość i zwrot wektora pola w rozważanym punkcie pola można otrzymać z wartości i kierunku maks. spadku potencjału w tymże punkcie (np.
 = -grad V, V — potencjał pola elektrostat.); jeśli rozważane pole zachowawcze jest polem siłowym (np. polem sił grawitacyjnych czy elektrostat.), to potencjał przedstawia sobą pracę przeniesienia ciała próbnego (np. próbnej masy lub próbnego dodatniego ładunku elektr.) przeciwko siłom danego pola od punktu odniesienia O do rozważanego punktu P pola (np. dla pola grawitacyjnego potencjał V = -GM/r, gdzie G — stała grawitacji, M — masa wytwarzająca pole grawitacyjne, r — odległość rozważanego punktu P od środka ciężkości masy M, przy tym za punkt odniesienia przyjęto tu punkt leżący w nieskończoności

NAPIĘCIE ELEKTRYCZNE - Wielkość fiz. skalarna, odnoszona do 2 dowolnych punktów (np. A i B) obwodu elektr. lub pola elektr., równa stosunkowi pracy W, wykonywanej przez siły pola elektr. przy przemieszczaniu ładunku elektr. q wzdłuż pewnej krzywej s (między dwoma wybranymi punktami pola), do wartości tego ładunku:
, gdzie E_s — składowa natężenia pola elektr. wzdłuż elementu drogi ds. W polu elektr. zachowawczym praca nie zależy od drogi, zatem napięcie elektryczne jest równe różnicy potencjałów w tych 2 punktach pola: U_AB  = φ(A) - φ(B).

Jednostką napięcia elektrycznego jest wolt

DIPOL ELEKTRYCZNY - Układ 2 jednakowych co do wartości, lecz przeciwnego znaku ładunków elektr. (+Q i -Q) znajdujących się w pewnej odległości l od siebie (np. cząsteczka o rozsuniętym ładunku elektr., tzw. spolaryzowana); wielkością charakteryzującą dipol elektryczny jest dipolowy moment elektryczny
, określony jako wektor skierowany od ładunku ujemnego do dodatniego o wartości µ = Q · l.

POLARYZACJA DIELEKTRYKA - Powstawanie elektr. momentu dipolowego dielektryka pod wpływem zewn. pola elektr. Rozróżnia się polaryzację dielektryka deformacyjną i orientacyjną. Polaryzacja orientacyjna (ustawienia) występuje w dielektrykach polarnych i jest wynikiem częściowego uporządkowania słabo związanych cząsteczek polarnych. Miarą polaryzacji dielektryka jest wektor polaryzacji
, określony jako stosunek całkowitego momentu elektr. dielektryka do jego objętości; dla substancji izotropowych
jest proporcjonalne do pola elektr. (ε₀ — przenikalność elektr. próżni, — podatność elektr. ośrodka).

POJEMNOŚĆ ELEKTRYCZNA - Jedna z podstawowych wielkości charakteryzujących elektr. właściwości przewodnika; pojemność elektryczna przewodnika jest równa stosunkowi ładunku q zgromadzonego na przewodniku do potencjału V wywołanego obecnością tego ładunku: C = q/V; zależy od kształtu i rozmiarów przewodnika oraz przenikalności elektr. otaczającego ośrodka. Całkowita pojemność elektryczna równolegle połączonych kondensatorów elektrycznych jest równa sumie ich pojemności elektrycznych: C = C₁ + C₂ +... + Cn; w przypadku kondensatorów połączonych szeregowo zachodzi związek 1/C = 1/C₁ + 1/C₂ +... + 1/Cn. Jednostką pojemności elektrycznej w układzie SI jest farad.

KONDENSATOR ELEKTRYCZNY - Układ 2 przewodników rozdzielonych warstwą dielektryka, służący do gromadzenia ładunku elektr.; kondemsator elektryczny ładuje się przez przyłączenie do źródła prądu stałego; na jego elektrodach gromadzi się wówczas ładunek elektr., a w dielektryku powstaje pole elektr. o energii

W = ¹/₂CU ²

gdzie: C — pojemność, U — napięcie między elektrodami

SIŁA LORENTZA - Siła
, z jaką pole elektromagnet. działa na poruszającą się cząstkę naładowaną:

= q
 + q
×

gdzie q — ładunek elektr. cząstki,
— natężenie pola elektr.,
— indukcja magnet.,
— prędkość cząstki; pierwszy składnik wzoru przedstawia siłę działającą na cząstkę w polu elektr., drugi — siłę działającą w polu magnet. (powoduje ona zakrzywienie toru cząstki);

DIPOL MAGNETYCZNY - Układ fiz. wytwarzający w przestrzeni takie pole magnet. jak 2 blisko siebie położone, przeciwnego znaku masy magnet. (ładunki magnet.; umowne odpowiedniki ładunku elektr. w magnesie trwałym); dipole magnetyczne złożone z mas magnet. w przyrodzie nie występują, w skali mikroskopowej dipolami magnetycznymi są cząstki elementarne o niezerowym spinie, w skali makroskopowej — magnesy sztabkowe, koliste obwody prądu elektr.; wielkością charakteryzującą dipol magnetyczny jest dipolowy moment magnetyczny.

WEKTOR WODZĄCY - Wektor wodzący - dla danego punktu A to wektor zaczepiony w początku układu współrzędnych i o końcu w punkcie A, czyli np. w układzie kartezjańskim: Długość wektora wodzącego jest odległością punktu od początku układu współrzędnych

ENERGIA KINETYCZNA BRYŁY SZTYWNEJ - Bryłą sztywną nazywamy takie ciało, w którym wszystkie punkty mają zawsze względem siebie stałą odległość. ENERGIA KINETYCZNA, część energii mech. układu fiz. (np. ciała sztywnego) zależna od prędkości jego punktów; w przypadku ciała sztywnego o masie m poruszającego się ruchem postępowym z prędkością v (znacznie mniejszą od prędkości światła) jego energia kinetyczna E _k = mv ²/2; energia kinetyczna ciała sztywnego obracającego się z prędkością kątową ω wokół pewnej osi E _k = Iω ²/2, gdzie I — moment bezwładności ciała względem tejże osi; wg

ZJAWISKO REZONANSU - Rezonans - zjawisko fizyczne zachodzące dla drgań wymuszonych, objawiające się pochłanianiem energii poprzez wykonywanie drgań o dużej amplitudzie przez układ drgający dla określonych częstotliwości drgań. Przedział częstości Δω dla której moc rozpraszana jest równa połowie mocy z maksimum jest nazywana szerokością rezonansu i jest równa odwrotności czasu zaniku (czasu życia) drgań:

DEFICYT MASY - Deficyt masy (niedobór masy, defekt masy) - różnica Δm między sumą mas nukleonów wchodzących w skład jądra atomowego, a masą jądra. Iloczyn niedoboru masy i kwadratu prędkości światła w próżni jest równy energii wiązania jądra, ΔE. E=MC²

ŹRÓDŁO ENERGII: REAKCJE FUZJI - Zjawisko tzw. fuzji zachodzi w trakcie syntezy atomów wodoru w hel. Takie reakcje zachodzą we wnętrzu każdej gwiazdy. Reaktor fuzyjny ma funkcjonować na zasadzie syntezy cząsteczek trytu z cząsteczkami deuteru. W wyniku syntezy powstaje wolny neutron, cząsteczka helu oraz energia. Do poprawnego działania reaktora potrzebne są potężne elektromagnesy mające na celu utrzymanie plazmy z dala od ścian reaktora. Do uruchomienia procesu syntezy potrzebna jest ogromna ilość energii. Reaktor po uruchomieniu będzie produkował więcej energii niż jej zużywał do podtrzymania reakcji.

ZALEŻNOŚĆ TEMPERATUROWA OPORU - Opór elektryczny typowych półprzewodników maleje ze wzrostem temperatury, głównie ze względu na silny, wykładniczy wzrost liczby nośników prądu ze wzrostem temperatury. Ruchliwość nośników zmienia się z reguły słabiej z temperaturą. Zależność temperaturowa oporu w przybliżeniu może być opisana funkcją: r(T) = A exp(a/T) , a w związku z tym T = a/(ln r(T) - lnA).

PRAWO GAUSSA DLA POLA MAGNETYCZNEGO - Całkowity strumień magnetyczny przechodzący przez powierzchnię zamkniętą równa się zeru. Fakt ten wynika stąd, iż pole magnetyczne jest bezźródłowe - nie istnieją w świecie ładunki magnetyczne, dywergencja pola jest wszędzie równa zero.

DIPOL MAGNETYCZNY, MAGNETYZACJA - Dipolem magnetycznym nazywamy układ dwóch biegunów magnetycznych, jednakowych co do wartości, ale przeciwnych znaków, znajdujących się w odległości l. Dipol magnetyczny charakteryzuje wielkość zwaną dipolowym momentem magnetycznym oznaczany przez p
, zdefiniowana w dalszej części pracy. Magnetyzacja jest właściwością pewnych materiałów (m. in. magnesów), która opisuje w jakim stopniu na pole magnetyczne wpływa na ten materiał, a także określa pole magnetyczne wytwarzane przez ten materiał. Magnetyzację definiuje się przez momenty magnetyczne w jednostce objętości. Pochodzenie momentów magnetycznych tworzących magnetyzację może być albo mikroskopową odpowiedzią na prądy elektryczne odpowiadające ruchowi elektronów w atomach albo spinów elektronowych.

---