Charakterystyka podstawowych parametrów analizy struktury

1. Charakterystyka miar tendencji centralnej (przeciętnych)

W analizie struktury interesuje nas nie tylko rozkład częstości kategorii wyróżnionej zmiennej, ale najczęściej pytamy o to, co jest typowe, np. jaka jest typowa (przeciętna) płaca górników, nauczycieli, z jak licznej rodziny pochodzi typowy student, jaka jest najczęściej wydajność pracy w badanym przedsiębiorstwie itp.

Na pytanie takie odpowiadamy stosując miary tendencji centralnej (przeciętnego poziomu).

Najczęściej stosowanymi miarami przeciętnego poziomu są:

• średnia arytmetyczna (średnia klasyczna),

• dominanta (przeciętna pozycyjna),

• kwantyle, wśród których najczęściej stosowane są kwartyle (przeciętne pozycyjne).

1.1 Średnia arytmetyczna

Średnia arytmetyczna jest najczęściej stosowaną klasyczną miarą tendencji centralnej.

Własności średniej są następujące:

• średnia jest obliczana na podstawie wszystkich obserwacji,

• średnia bardzo dobrze nadaje się do porównywania dwóch lub większej liczby zbiorowości,

• suma odchyleń wszystkich wartości zmiennej od jej średniej arytmetycznej jest zawsze równa zero:

,

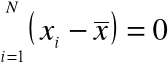
• suma kwadratów odchyleń wartości zmiennej od średniej arytmetycznej jest mniejsza niż suma kwadratów odchyleń od jakiejkolwiek innej stałej,

• średnia może przyjmować wartości ułamkowe nawet wtedy, kiedy zmienna przyjmuje tylko wartości całkowite,

• średnia nie może być obliczana, jeśli skrajne przedziały zmiennej są otwarte,

• na wielkość średniej arytmetycznej silny wpływ mają skrajne wartości cechy.

Wyróżnia się średnią arytmetyczną:

• prostą - stosowaną w przypadku szeregów prostych (wyliczających),

• ważoną - stosowaną w przypadku danych pogrupowanych (szeregi rozdzielcze).

Im rozkład zmiennej jest bardziej zbliżony do symetrycznego, tym większą wartość poznawczą ma średnia arytmetyczna. I odwrotnie, im rozkład jest bardziej asymetryczny, tym lepiej tendencję centralną wyraża mediana, a nie średnia arytmetyczna.

W przypadku rozkładów o stosunkowo dużej asymetrii najlepiej uwzględnić obydwa te parametry.

Średnia arytmetyczna

1. W przypadku szeregów prostych

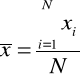
2. W przypadku szeregów rozdzielczych z przedziałami

jednostkowymi

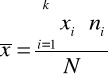
gdzie: k - liczba przedziałów klasowych w schemacie klasyfikacyjnym

3. W szeregach rozdzielczych z równymi przedziałami klasowymi

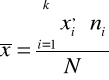
1.2 Dominanta

Dominanta, zwana również modalną, jest to „wartość” cechy, która występuje w zbiorowości najczęściej. Największą zaletą dominanty jest łatwość jej ustalenia i interpretacji. Dominanta nie zawsze jednak będzie dawać najlepszy opis danych, gdyż:

• kategoria występująca najczęściej może nie występować dużo częściej od innych kategorii,

• rozkład badanej cechy może nie mieć jednej, wyraźnej dominanty. Mówi się wtedy o rozkładzie wielomodalnym. Może też charakteryzować się równomierną liczebnością poszczególnych kategorii i w ogóle nie mieć dominanty.

• dominanta jest podatna na sposób kategoryzacji zmiennej i łączenie kategorii.

Pomimo tych wad, dominanta jest bardzo często używaną miarą przeciętnego poziomu i można ją ustalać dla cechy jakościowej i ilościowej.

Dominanta - modalna

1. W przypadku szeregów prostych oraz szeregów rozdzielczych z przedziałami jednostkowymi

dominantą jest poziom cechy występujący najczęściej

2. W przypadku szeregów rozdzielczych (z przedziałami równymi i nierównymi) ustalamy, w którym przedziale jest najwięcej jednostek. Jest to przedział dominujący - oznaczmy go przez m. Z tego przedziału wyliczamy wartość dominanty według wzoru:

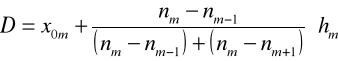
1. Mediana i kwartyle

Mediana, czyli kwartyl drugi (Me lub Q₂) jest kategorią cechy, która dzieli zbiorowość na połowy, z których każda zawiera po 50% obserwacji. Walory mediany (poznawcze) rosną wraz ze wzrostem liczby obserwacji oraz liczby kategorii (wariantów) zmiennej. Mediana (wartość środkowa) wskazuje więc wartość środkowej obserwacji w bazie danych, uporządkowanej ze względu na badaną cechę.

Mediana jest odporna na wpływ obserwacji o skrajnych wartościach cechy, można ją obliczać nawet wówczas, gdy krańce rozkładu są otwarte.

Suma bezwzględnych wartości różnic pomiędzy wartościami danej zmiennej dla wszystkich obserwacji a medianą jest najmniejsza ze wszystkich sum bezwzględnych wartości różnic pomiędzy wartościami wszystkich obserwacji a jakąkolwiek stałą.

Podobny sens do mediany mają kwartyle: Q₁ oraz Q₃.

Kwartylem pierwszym (dolnym) Q₁ nazywamy taką wartość cechy (taką kategorię cechy), poniżej której leży 25% jednostek zbiorowości.

Kwartyl trzeci (górny) to taka wartość cechy, która dzieli zbiorowość na dwie części i to takie, że 75% jednostek ma wartości nie większe od Q₃.

Pomiędzy Q₁ i Q₃ leży 50% obserwacji, które można nazwać typowym obszarem zmienności.

Mediana (kwartyl drugi) - wartość środkowa

1. W przypadku szeregów prostych

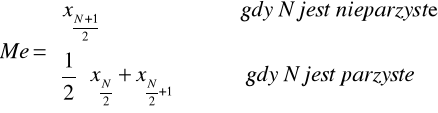
2. W przypadku szeregów rozdzielczych

Na podstawie kolumny liczebności skumulowanych ustalamy, w którym przedziale jest mediana - załóżmy, że jest to przedział m. Medianę wyliczamy z tego przedziału według wzoru:

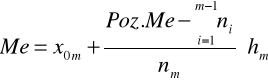
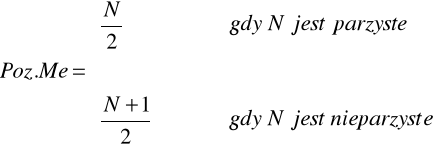
− dolna granica przedziału m, w którym występuje mediana,

− skumulowana liczebność do przedziału poprzedzającego przedział zawierający medianę

n_m − liczba jednostek w przedziale z medianą

h_m − rozpiętość przedziału, w którym jest mediana.

Kwartyle

1. Kwartyl 1 - jego pozycja to N podzielone przez 4

Na podstawie kolumny liczebności skumulowanych ustalamy, w którym przedziale jest kwartyl 1 - załóżmy, że jest to przedział m. Kwartyl 1 wyliczamy z tego przedziału według wzoru:

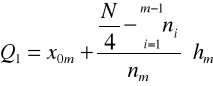
2. Kwartyl 3 - jego pozycja to 3N/4

Na podstawie kolumny liczebności skumulowanych ustalamy, w którym przedziale jest kwartyl 3 - załóżmy, że jest to przedział m. Kwartyl 3 wyliczamy z tego przedziału według wzoru:

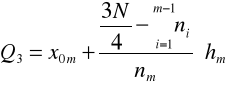
2. Charakterystyka miar dyspersji

Rozkłady empiryczne charakteryzują się nie tylko tendencją centralną, ale też określonym zróżnicowaniem (rozproszeniem). Możemy spotkać rozkłady o tej samej tendencji centralnej, ale o różnej zmienności. Do jej pomiaru stosuje się miary dyspersji.

2.1. Wariancja i odchylenie standardowe

Parametry te należą do najważniejszych miar statystycznych.

Interpretację merytoryczną posiada odchylenie standardowe. Określa ono, o ile przeciętnie biorąc, poszczególne wartości cechy odchylają się +/- od średniej arytmetycznej. Posiada następujące właściwości:

• jest bardzo wrażliwe na wartości skrajne cechy,

• obliczamy je na podstawie wszystkich obserwacji,

• wyrażone jest w jednostkach miary analizowanej zmiennej,

• jest największe wówczas, gdy połowa obserwacji ma wartość maksymalną, a połowa minimalną. Wynosi ono wtedy:

.

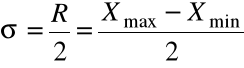
Odchylenie standardowe

1. W przypadku szeregów wyliczających (prostych)

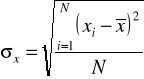
lub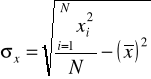

2. W przypadku szeregów rozdzielczych z przedziałami jednostkowymi

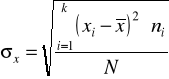
lub

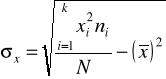
3. W szeregach rozdzielczych z równymi przedziałami klasowymi

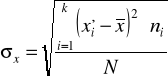
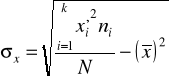
Wariancja

1. W przypadku szeregów wyliczających (prostych)

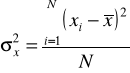
2. W przypadku szeregów rozdzielczych z przedziałami jednostkowymi

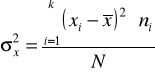
3. W szeregach rozdzielczych z równymi przedziałami klasowymi

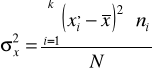
Odchylenie standardowe wykorzystujemy do określania:

− typowego obszaru zmienności

− obszaru zmienności wynikającego z reguły trzech sigm

,

Odchylenie standardowe służy też do standaryzacji zmiennych, która pozwala na wyeliminowanie wpływu jednostek miary na rozkład zmiennej. Standaryzację przeprowadza się według wzoru:

,

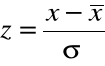
Zmienna standaryzowana ma średnią 0 i odchylenie standardowe równe 1.

2.2 Klasyczny współczynnik zmienności

Dla porównania rozproszenia różnych zmiennych stosujemy względną miarę zmienności zwaną klasycznym współczynnikiem zmienności. Jest to miara niezmienna względem skali. Pozwala ustalić jaki procent średniej stanowi odchylenie standardowe. Współczynnik ten liczymy według wzoru:

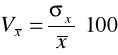
Współczynnik ten wyrażamy najczęściej w % i im jest on większy, tym dyspersja rozkładu jest silniejsza. Umownie przyjmuje się, że:

− jeśli
% - dyspersja słaba,

− jeśli
% - dyspersja umiarkowana,

− jeśli
% - dyspersja silna,

− jeśli
% - dyspersja bardzo silna.

2.3 Odchylenie ćwiartkowe i pozycyjny współczynnik zmienności

Odchylenie ćwiartkowe stosujemy, gdy chcemy wyeliminować silny wpływ obserwacji skrajnych

Obliczamy je, korzystając z rozstępu ćwiartkowego:
, według wzoru:

.

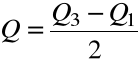
Q informuje o tym, jakie jest przeciętne rozproszenie typowych obserwacji wokół mediany (wokół środka rozkładu).

Dla uniezależnienia pomiaru dyspersji od jednostek miary, w jakich wyrażona jest cecha stosujemy pozycyjny współczynnik dyspersji:

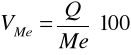
Pozycyjny współczynnik zmienności określa, jaką część (procent) mediany stanowi odchylenie ćwiartkowe.

Im jego wartość jest większa, tym dyspersja rozkładu jest silniejsza.

Do oceny dyspersji można też stosować miary oparte na decylach.

Czasami do pomiaru względnej dyspersji używa się współczynnika zmienności określonego wzorem:

.

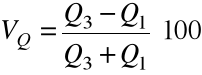
Jego interpretacja jest podobna jak współczynnika V_Me, mianowicie, im jego wartość jest większa, tym dyspersja badanej cechy jest silniejsza

3. Miary asymetrii

Pozwalają one na określenie, jakie jednostki w zbiorowości przeważają: czy jednostki o wartościach cechy poniżej czy też powyżej tendencji centralnej.

Biorąc powyższe pod uwagę, wyróżnia się:

a) rozkład symetryczny, w którym taka sama liczba jednostek ma wartości cechy poniżej jak i powyżej średniej arytmetycznej. W rozkładzie tym trzy podstawowe miary przeciętne: średnia, mediana i dominanta są identyczne:

b) rozkład prawostronnie asymetryczny, w którym przeważają jednostki o wartościach cechy mniejszych od średniej arytmetycznej

c) rozkład lewostronnie asymetryczny, w którym występuje przewaga jednostek o wartościach cechy powyżej średniej arytmetycznej.

Do pomiaru natężenia i kierunku asymetrii służą współczynniki asymetrii. Najczęściej stosowane są:

• klasyczno - pozycyjny współczynnik asymetrii obliczany wg wzoru:

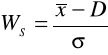
W_S = 0 - rozkład symetryczny,

W_S > 0 - rozkład prawostronnie asymetryczny,

W_S < 0 - rozkład lewostronnie asymetryczny.

Jeśli przy tym : W_S
− to asymetria oceniana jest jako słaba,

W_S
− asymetria umiarkowana

W_S
− rozkład silnie asymetryczny.

Warto też wskazać, że w rozkładzie cech ciągłych umiarkowanie asymetrycznym zachodzi następująca równość:

Wzór ten pozwala na ustalenie przybliżonej wartości jednej z trzech przeciętnych, jeśli dwie pozostałe są znane.

• pozycyjny współczynnik asymetrii liczymy korzystając ze wzoru:

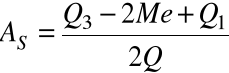
Miernik ten jest unormowany na przedziale
.

Przyjmuje wartość równą zero tylko wtedy, gdy rozkład jest symetryczny.

Przy jego interpretacji, jako punkt odniesienia uwzględniamy medianę, a nie średnią arytmetyczną.

• klasyczną miarą asymetrii jest standaryzowany trzeci moment centralny.

Najczęściej w oparciu o podane informacje o wartościach cechy liczymy moment trzeci centralny według wzoru:

,

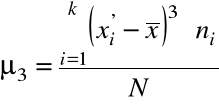
a następnie liczymy moment standaryzowany:

.

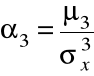
Interpretacja tego miernika jest identyczna jak wcześniej omówionego klasyczno-pozycyjnego współczynnika zmienności.

4. Miary koncentracji (skupienia)

Koncentrację wokół wartości średniej określa się mianem kurtozy. Jako względną miarę koncentracji stosuje się czwarty moment centralny wyrażony w jednostkach odchylenia standardowego.

Procedura jego liczenia jest podobna do procedury liczenia klasycznej miary asymetrii. Najpierw w oparciu o zebrane informacje liczymy czwarty moment centralny:

,

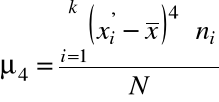
a następnie współczynnik koncentracji, według wzoru:

.

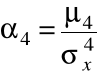
Interpretacja tego współczynnika jest następująca:

₄ < 3 − rozkład badanej cechy jest spłaszczony, tzn. o koncentracji wokół średniej mniejszej aniżeli w rozkładzie normalnym,

₄ = 3 − rozkład o koncentracji takiej jak w rozkładzie normalnym,

₄ > 3 − rozkład jest wysmukły, tzn. o koncentracji wokół średniej większej niż w rozkładzie normalnym.

---