SPRAWOZDANIE Z LABORATORIUM Teorii Obwodów
	Nr grupy lab.:	Termin:	Data wyk. ćw.
Ćwiczenie nr 1 Podstawowe twierdzenia teorii obwodów			Ocena

Spis przyrządów laboratoryjnych:

• Generator funkcyjny POF - 10

• Miernik fazy PM - 100

• Multimetr V-640

• Częstościomierz C - 549 A

• Dekada rezystancyjna DR4b - 16

• Dekada kondensatorowa DK - 50

• Dekada indukcyjna

• Zestaw laboratoryjny Z2/2

• Miernik impedancji BM - 507

1. Zasada superpozycji

Dołączono do panelu wskazany przez prowadzącego dwójnik o impedancji Z (rys. 1). Z przedziału 0,5 ÷ 2,5 kHz wybrano częstotliwość, przy której będą prowadzone dalsze pomiary w trakcie całego ćwiczenia. Ustawiono poziom napięcia z generatora G tak, aby na rozwartych zaciskach panelu (A - B) było napięcie około 500 mV (przy włączonym E₁). Podczas weryfikacji pomiarowej zasady superpozycji korzystano z układu pomiarowego przedstawionego na rys. 1.

Rys. 1

Warunki pomiarowe i parametry zastosowanych elementów, wskazanych przez prowadzącego:

• częstotliwość f = 800 Hz

• dwójnik RC: R = 600 Ω, C = 0,8 μF.

• Weryfikacja pomiarowa metody superpozycji, przed dołączeniem dwójnika RC.

Przed dołączeniem do zacisków A - B układu pomiarowego, dwójnika RC o impedancji Z, ustawiono taką wartość napięcia generatora, dla której napięcie U₁ = 500 mV na rozwartych zaciskach układu przy włączonym źródle E₁ (K₁ w pozycji a, K₂ w pozycji b). Następnie przeprowadzono pomiary napięcia i fazy na rozwartych zaciskach panelu.

• Pomiar napięcia
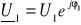
  gdy włączone jest źródło E₁ (K₁ w pozycji a), a rezystor R_g2 jest jednym zaciskiem dołączony do masy (K₂ w pozycji b).

• Pomiar napięcia
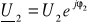
  gdy włączone jest źródło E₂ (K₂ w pozycji a), a rezystor R_g1 jest jednym zaciskiem dołączony do masy (K₁ w pozycji b).

• Pomiar napięcia
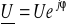
  gdy włączone są obydwa źródła (K₁ i K₂ w pozycji a).

Sprawdzenie zasady superpozycji:

zatem:

Wnioski przedstawiono poniżej.

• Weryfikacja pomiarowa metody superpozycji, po dołączeniu dwójnika RC.

Korzystając dalej z układu pomiarowego rys. 1 dołączono do zacisków A - B dwójnik RC o impedancji Z i dokonano weryfikacji pomiarowej metody superpozycji mierząc napięcia i fazy na zaciskach tegoż dwójnika.

• Pomiar napięcia
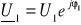
  gdy włączone jest źródło E₁ (K₁ w pozycji a), a rezystor R_g2 jest jednym zaciskiem dołączony do masy (K₂ w pozycji b).

• Pomiar napięcia
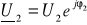
  gdy włączone jest źródło E₂ (K₂ w pozycji a), a rezystor R_g1 jest jednym zaciskiem dołączony do masy (K₁ w pozycji b).

• Pomiar napięcia
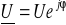
  gdy włączone są obydwa źródła (K₁ i K₂ w pozycji a).

Sprawdzenie zasady superpozycji:

zatem:

Wnioski i uwagi:

Wyniki dokonanych pomiarów pokrywają się z wynikami obliczeń opierających się na zasadzie superpozycji. Można, zatem stwierdzić zgodność teorii z praktyką.

Rozbieżności w otrzymanych wynikach obliczeń są pomijalnie małe. Wynikają z zaokrągleń wyniku oraz z niedokładnością przyrządów użytych w ćwiczeniu. Podsumowując: zasada superpozycji jest własnością układów liniowych i może być uważana za właściwość definiującą tę klasę układów, tzn. można uważać, że obwód jest liniowy, jeśli słuszna jest dla niego zasada superpozycji.

2. Twierdzenie Thevenina

2.1. - 2. Wyznaczenie impedancji zastępczej układu Z_z.

Podłączono źródło E₁, a rezystor R_g2 dołączono jednym zaciskiem do masy. Zmierzono napięcie
pomiędzy rozwartymi zaciskami wyjściowymi. Następnie dołączono do układu rezystor R_p, o rezystancji wybranej z przedziału (100 ÷ 1000) Ω tak, aby
. A następnie zmierzono napięcie
i obliczono impedancję zastępczą. Do pomiaru układ pomiarowy, którego schemat został zamieszczony na rys. 2.

Rys. 2

Dobrano R_p = 670 Ω

Korzystając ze wzoru obliczono impedancję zastępczą układu.

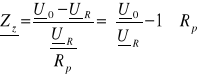
Pomiary i obliczenia powtórzono dla konfiguracji układu dla włączonego źródła E₂ oraz

E₁ + E_2.

• Pomiar napięć U₀ i U_R, gdy włączone jest źródło E₁ (K₁ w pozycji a), a rezystor R_g2 jest jednym zaciskiem dołączony do masy (K₂ w pozycji b).

zatem:

• Pomiar napięć U₀ i U_R, gdy włączone jest źródło E₂ (K₂ w pozycji a), a rezystor R_g1 jest jednym zaciskiem dołączony do masy (K₁ w pozycji b).

zatem:

• Pomiar napięć U₀ i U_R, gdy włączone są obydwa źródła (K₁ i K₂ w pozycji a).

zatem:

2.3. Wyznaczenie impedancji zastępczej układu Z_z za pomocą miernika impedancji.

Odłączono generator i inne przyrządy pomiarowe, a obydwa rezystory R_g1 i R_g2 dołączono do masy, następnie zmierzono impedancję dwójnika Z_Z za pomocą miernika impedancji dla wybranej w ćwiczeniu częstotliwości. Następnie porównano z wynikami uzyskanymi w p. 2.0 2.1, 2.2.

• Pomiar za pomocą miernika impedancji:

• Wyniki pomiarów z punktów odpowiednio:

Wnioski i uwagi:

Wynik pomiar impedancji za pomocą miernika impedancji okazał się dość zbliżony, a w pewnym przybliżeniu niemal identyczny do wyników uzyskanych w postaci obliczeń w poprzednim punkcie. Zatem wywnioskować można ze wynik nie zależy od napięcia lecz od częstotliwości, sygnału.

2.4. Budowa układu zastępczego. Weryfikacja pomiarowa twierdzenia Thevenina.

Zbudowano układ zastępczy wykorzystując odpowiedni panel na stanowisku, układ jak na rys. 3, przy czym:
, które zostało zmierzone w punkcie 2.3, natomiast impedancja
wyznaczona w punkcje 1.1. Wartość skuteczną napięcia E_Z uczyniono równą wartości skuteczniej napięcia U₀ zmierzonej w punkcie 2.1, a następnie zmierzono napięcie
mierząc fazę względem napięcia E_Z.

Rys. 3.

Obliczenie parametrów obwodu:

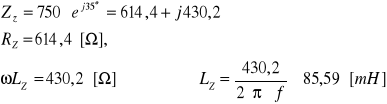
Pomiar napięcia
.

zatem:

Wnioski i uwagi:

Twierdzenie Thevenina pozwala skonstruować układ równoważny na zaciskach wyjściowych układowi o nieznanej strukturze wewnętrznej. Można zauważyć, że mimo drobnych niedokładności w obliczeniach przeprowadzonych na ćwiczeniu, twierdzenie Thevenina potwierdziło się z dużą dokładnością - praktycznie brak znaczących różnicy w wartości napięcia mierzonego na zaciskach układu o nieznanej strukturze i w wartości napięcia mierzonego na zaciskach układu symulującego układ nieznany. Można z tego wysnuć wniosek, że aby dobrze zasymulować nieznany układ nie jest potrzebna bardzo duża dokładność obliczenia wartości elementu rezystancyjnego i reaktancyjnego - liczy się rząd tych wielkości, a nieco mniejsza dokładność nie wprowadza istotnego błędu.

3. Dopasowanie na maksimum mocy czynnej.

Wyznaczono elementy dwójnika RC, które zapewniają dopasowanie na maksimum mocy czynnej:
. Dołączono do panelu dwójnik RC (rys. 4) o rezystancji R = R₀. Zmierzono ponownie napięcia biegu luzem na panelu w przypadku, kiedy działają odpowiednio źródła E₁, E₂, E₁ + E₂.

Rys. 4.

• Pomiar napięcia, gdy włączone jest źródło E₁ (K₁ w pozycji a), a rezystor R_g2 jest jednym zaciskiem dołączony do masy (K₂ w pozycji b).

• Pomiar napięcia, gdy włączone jest źródło E₂ (K₂ w pozycji a), a rezystor R_g1 jest jednym zaciskiem dołączony do masy (K₁ w pozycji b).

• Pomiar napięcia, gdy włączone są obydwa źródła (K₁ i K₂ w pozycji a).

Następnie wyznaczono elementy dwójnika RC, które zapewniają dopasowanie na maksimum mocy czynnej, czyli aby spełnione było równanie:

Stąd:

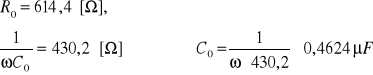
3.1. Wyznaczenie mocy czynnej na rezystorze, przy różnych wartościach pojemności dołączonego dwójnika RC.

Do zacisków panelu dołączono dwójnik RC, (rys. 4). Zmieniając pojemność C dołączonego dwójnika w szerokim zakresie, C = 10 μF pierwsza wartość, oraz następne zgodnie ze wzorem
dla (k = 1, 2, 4, 6, 8, 10, 12, 15, 20, 25, 30, 35, 40, gdzie C_p jest zaokrąglona wartością C₀). Mierzono napięcie U_R na rezystorze R, gdy włączone jest źródło E₁, a rezystor R_g2 jest jednym zaciskiem dołączony do masy.

Wyniki pomiaru zostały przedstawione w tabeli 1. oraz na wykresie 1.

Lp.	k	C	XC	UR	P
				[µF]	[Ω]	[mV]	[µW]
1	1	4,624	43,02	244	96,9
2	2	2,312	86,05	247	99,3
3	4	1,156	172,1	250	102
4	6	0,7707	258,1	253	104
5	8	0,578	344,2	255	106
6	10	0,4624	430,2	256	107
7	12	0,3853	516,3	253	104
8	15	0,3083	645,3	250	102
9	20	0,2312	860,5	240	93,8
10	25	0,1849	1076	227	83,9
11	30	0,1541	1291	209	71,1
12	35	0,1321	1506	192	60,0
13	40	0,1156	1721	178	51,6

Wnioski i uwagi:

Odczytana z wykresu wartość, dla której maksymalna moc czynna P wynosi X_c = 432,2, zatem odpowiada to wartości C_max = 0,4624, a następnie porównując tą wartości z C₀ okazuje się, że one identyczne. Wniosek nasuwa się automatycznie analizując kształt wykresu okazuje się, że związany jest z tym, że dwójnik ma impedancję
. Ponieważ
, zatem przy określonej częstotliwości reaktancja pojemnościowa zmienia się od 0 do
. Gdy
jest bliskie zeru wówczas napięcie na rezystorze będzie największe, ponieważ całe napięcie odłoży się na nim. Natomiast, gdy
będzie wartością bardzo dużą, wtedy większość napięcia odłoży się na kondensatorze a napięcie na rezystorze będzie bliskie zeru. Zależność tę można zaobserwować analizując dane w tabeli 1 oraz „Wykres 1”.

3.2. Wyznaczenie mocy czynnej na rezystorze, przy różnych wartościach rezystancji dołączonego dwójnika RC.

Układ został obciążony dwójnikiem RC jak w punkcie 3.1. Zmieniano rezystancję R tego dwójnika w zakresie od 0.1 R₀ do 5 R₀, przy C = C₀. Mierzono napięcie U_R na rezystorze oraz obliczano moc czynną wydzielaną na nim, gdy:

1. jest włączone źródło E₁, a rezystor R_g2 jest jednym zaciskiem dołączony do masy,

2. jest włączone źródło E₂, a rezystor R_g1 jest jednym zaciskiem dołączony do masy,

3. są włączone obydwa źródła.

Wyniki pomiaru zostały przedstawione w tabeli 2, oraz na wykresie 2.

Lp.	R	UA	PA	UB	PB	UC	PC
		[Ω]	[mV]	[µW]	[V]	[µW]	[mV]	[µW]
1	61	47	36,2	24	9,4	27	12,0
2	111	81	59,1	46	19,1	49	21,6
3	211	132	82,6	71	23,9	79	29,6
4	311	172	95,1	93	27,8	101	32,8
5	361	190	100,0	101	28,3	111	34,1
6	411	207	104,3	109	28,9	120	35,0
7	461	219	104,0	116	29,2	128	35,5
8	511	232	105,3	122	29,1	134	35,1
9	561	243	105,3	128	29,2	141	35,4
10	611	254	105,6	133	29,0	149	36,3
11	661	263	104,6	139	29,2	152	35,0
12	711	272	104,1	142	28,4	159	35,6
13	761	281	103,8	148	28,8	162	34,5
14	811	290	103,7	151	28,1	168	34,8
15	861	297	102,4	155	27,9	171	34,0
16	911	304	101,4	159	27,8	176	34,0
17	961	310	100,0	161	27,0	179	33,3
18	1011	317	99,4	165	26,9	182	32,8
19	1061	321	97,1	169	26,9	186	32,6
20	1111	328	96,8	170	26,0	189	32,2
Lp.	R	UA	PA	UB	PB	UC	PC
		[Ω]	[mV]	[µW]	[V]	[µW]	[mV]	[µW]
21	1161	332	94,9	172	25,5	191	31,4
22	1211	338	94,3	176	25,6	194	31,1
23	1261	341	92,2	179	25,4	198	31,1
24	1311	347	91,8	180	24,7	199	30,2
25	1361	350	90,0	181	24,1	201	29,7
26	1411	352	87,8	183	23,7	204	29,5
27	1511	360	85,8	188	23,4	208	28,6
28	1611	368	84,1	191	22,6	211	27,6
29	1711	372	80,9	193	21,8	215	27,0
30	1811	379	79,3	198	21,6	219	26,5
31	1911	383	76,8	199	20,7	220	25,3
32	2011	389	75,2	201	20,1	222	24,5
33	2111	392	72,8	202	19,3	226	24,2
34	2211	398	71,6	206	19,2	229	23,7
35	2311	400	69,2	209	18,9	230	22,9
36	2411	403	67,4	210	18,3	232	22,3
37	2511	408	66,3	211	17,7	234	21,8
38	2711	412	62,6	213	16,7	238	20,9
39	3000	420	58,8	219	16,0	241	19,4

Wnioski i uwagi:

„Wykres 2” przedstawia zmiany wartości mocy wydzielonej w rezystorze spowodowane zmianami wartości tego rezystora dla trzech pozycji włączników. Wykresy mają kształt paraboloidy o maksimum w punkcie R ≈ 614,4 Ω. Wartość ta dokładnie odpowiada części rzeczywistej wyznaczonej wcześniej wartości impedancji dopasowania.

1

---