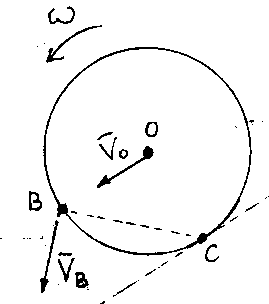
13.Tarcza Stacza Się Ze stała predkoscia V_o po równi pochyłej nachylonej do poziomu pod katem alfa. Znaleźć prędkość prędkość przyspieszenie punktu B, jeśli r=2[m], V_o=1,5[m/s²] a kąt alfa = 30^o

C-chwilowy srodek obrotu

14. Wyznaczyć chwilowy środek obrotu i prędkość kątową pręta, jeśli V_A=2[m/s] r=0,5[m].

C= chwilowy srodek obrotu

15 Ramka prostokątna obraca się dookoła nieruchomego boku AD ze stała prędkością kątową omega = 4[rad/s]. Wzdłuż boku AB porusza się punkt materialny z prędkością V=2[m/s]. Wyznacz przyspieszenie Coriolisa

16 Koła o promieniu R obraca się w swej płaszczyźnie wokół stałego punktu O ze stała prędkością kątową omega. Po obwodzie koła przesuwa się punktu z prędkością V_w =const. Obliczyć bezwzględne przyspieszenie punktu w położeniu A.

17. Punkt materialny o masie m=0,1[kg] porusza się pod działaniem siły : F_x=-2sin3t [N] , F_y= -2cos3t[N]. Określ tor tego punktu.

W tresci zadania nie ma podanych warunków początkowych na podstawie których można wyznaczyc stałe C, C_1,C₂, C₃. Wobec tego przyjmiemy, ze stałe te są równe 0.

k

18 Punkt materialny o masie m=2[kg] porusza się zgodnie z równaniami x(t)= hcos(omega*t) , y(t)= hsin (omega*t). znaleźć : a.tor punktu b. prędkość oraz prędkość prędkość chwili t₁= Pi/omega, c. przyspieszenie w chwili t₂= 2Pi/omega, d. siłe działająca na ten punkt oraz jej wartość w chwili t₂ . h=0,05[m].

19 Jaki musi być współczynnik tarcia `mi' samochodu o drogę jeśli przy prędkości V=72[km/h] samochód ma się zatrzymać w ciągu t=6[s] od początku hamowania.

Dynamiczne równania ruchu :

20 Suwak obrabiarki o masie M=0,6[kg] będąc w stanie spoczynku został wprawiony w ruch wzdłuż prowadnicy za pomoca siły Q= 10[N] skierowanej do osi prowadnicy pod kątem alfa= 30^o Jaką prędkość uzyska suwak po przesunieciu go na odległość s=1[m] jeżeli współczynnik tarcia suwak-prowadnica wynosi `mi'=0,2?.

Równanie sil wzdłuż osi poziomej:

Równanie sił wzdłuż osi pionowej:

21. Pocisk o masie m wystrzelono pionowo w góre z prędkością początkową V_o. Wiedząc że siła oporu powietrza jest w postaci R=kV(k-stały współczynnik V-predkosc pocisku), wyznaczyc czas po którym pocisk osiągnie maksymalna wysokość.

Dynamiczne równanie ruchu wzdłuż osi pionowej:

22. Dla układu mas M i m połączonych nierozciągliwą i lekką nicią wyznaczyc ich przyspieszenie oraz naciąg nici. Ciało o masie M spoczywa na chropowatej równi pochyłej o kącie nachylenia alfa , współczynnik tarcia rowni wynosi `mi'.

Dynamiczne równania ruchu dla ciała o masie M : a*M= F-T-S gdzie S naciąg nici T- tarcie

F=Psin(alfa)=MgSin(alfa)

T=N*'mi'= Mg'mi'cos(alfa).

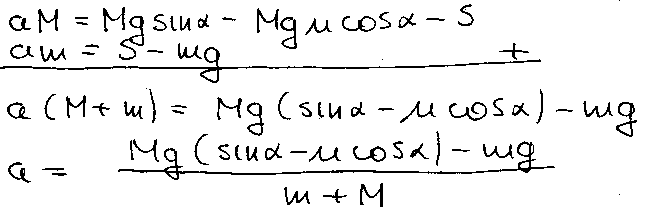
aM=Mgsin(alfa)- Mg'mi'cos(alfa)- S

23. Z jakim przyspieszeniem musi poruszać sie klin dolny aby klin górny nie zsuwał się względem dolnego. Miedzy powierzchniami styku klinów wystepuje tarcie. Kąt pochylenia klina dolnego =alfa.

24.Winda towarowa o cieżaze Q=6[T] opuszcza się z prędkością V=12[m/s]. Jaka siłe tarcie o ściny szybu powinien rozwijac hamulec bezpieczeństwa aby mogł zatrzymac winde na odcinku drogi s= 10[m] gdy lina na której wisi urwie się? Przyjąc ze siła tarcia jest stała.

25.W przekładnie zębatej koło 1 jest nieruchome. Do ramienia O₁,O₃ przyłożono moment siły M=0,2[Nm] Przekładnia jest ustawiona w płaszczyźnie poziomej. Wyznaczyc równanie ruchu układu i przyspieszenie katowe ramienia O₁O₃ jeśli masa każdego koła m=2 [kg] a promien r=0,2[m]. Mase ramienia i opory ruchu pomijamy.

26 Pozioma chropowata tarcza obraca się ze stała prędkością kątową `w<sub>0</sub> ` wokuł pionowej nieruchomej osi. Na tarczy w odległości r od osi obrotu znajduje się punkt materialny o masie m. Wyznaczyc maksymalną prędkość katowa tarczy `w_max' przy której nie zachodzi poślizg punktu.

27 Kula o masie m stacza się po równi kołowej o promieniu r bez prędkości początkowej z punktu A.Znaleźc reakcje równi gdy kula będzie mijała punkt B.

28 Lufa dziął jest pozioma a działo ma ciężar G=11000[N]. Ciężar pocisku wynosi P=5,5[N] Prędkość pocisku u wylotu lufy wynosi V=900[m/s]. O ile i w która stronę przesunie się działo jeżeli opory jego ruchu są równe 0,1G.

29. Pocisk artyleryjski o masie m=30[kg] wylatuje z lufy armaty z prędkością V=50[m/s]. Jaka jest siła odrzutu działająca na armate jeśli lot pocisku w lufie trwa 0,1[s].

30 Dwie kule jedna o masie m₁200[g] a druga o masie m₂300[g] poruszaja się do siebie wzdłuż lini prostej z prędkościami odpowiednio V₁=0,5[m/s] i V₂= 0,4[m/s]. Pewnej chwili zderzyły się i następnie poruszają się razem. Znaleźć : wspólna prędkość oraz kierunek ruchu.

31 Punkt o masie m jest zamocowany do nieważchiej i nierozciągliwej nici i porusz się po okręgu o promieniu r_o ze stała prędkością kątową `w₀'. Następnie nic została wciągnięta do otworu i punkt porusz się po okręgu o promieniu 0,5r₀ . Pomijając opory ruchu obliczyć w jaki stopniu zmieni się naciąg nici.

33. Wagonik o masie m=10³ [kg] jedzie z prędkością V=36[km/h] po torze prostym poziomym i uderza o zderzak. Jaka musi być sztywność sprężyny zderzaka aby jego ugiecie e=0,5[m]. Zakladamy liniowa charakterystyke sprężyny i brak strat energii mechanicznej.

V=36[km/h]=10[m/s]

34Ile wynosi energi kinetyczna płyty kwadratowej o boku a i masie m wirującej z prędkością kątową `w₀'=const wokuł swego nieruchomego boku

35Mała kula o masie M=1[kg] wykonuje ruch harmoniczny g(t)=12sin2t (gdzie g- w metrach t-seku ). Obliczyc energie mechaniczna kuli jeśli sztywność sprężyny na której jest oparta kula k=4[N/m].

36 Zwysokosci h=10[m] spada klocek o masie m=5[kg]. Ile procent energii kinetycznej zostało przez ten klocek stracone w wyniku oporu powietrza . Jeśli przy zetknieciu z ziemia prędkość klocka była równa V=10[m/s]

37. Kula o cieżaże Q=2[Kg] zawieszona na nieważkiej lince o długości l=1[m] uzyskała wskutek udeżenia prędkość prędkość=5[m/s]. Oblicz siłe w lince bezpośrednio po udeżeniu . Podaj wyniki obliczenia z dokładnością do 0,01[N].

38 Obliczyc przesuniecie pływającego żurawia przenoszącego ciężar P₁=2[T] jeśli wysięgnik z pozycji pionowej obruci się o kąt `'alfa'=30^o Ciężar zurawia P₂= 20[T] . Długosc wysięgnika OA=l=8[m]. Opur wody i ciężar wysięgnika pominąc

39 Wyznaczyc równanie małych drgan swobodnych preta jednorodnego długości l=1[m], zamocowanego obrotowo w punkcie A i wykonującego ruch w płaszczyźnie pionowej. Obliczyc okres tych drgan.

40 Koło o promieniu r=0,3[m] i masie m=20[kg] może toczyc się bez poślizgu w płaszczyźnie pionowej po prostej poziomej x. Srodek koła został połączony przegubem walcowym z dwiema poziomymi sprężynami o sztywności k i 2k, przy czym k=10³ [N/m]. Po przetoczeniu koła z położenia równowagi (w lewo lub w prawo ) i pozostawieniu go zacznie ono wykonywac ruch drgającym Wyprowadzic równanie ruchu tego koła i obliczyć częstotliwość jego drgan własnych.

3

---