Dopełnienie matematyczne
Granica, ciągłość i pochodna.
Omówimy pewne szczegóły analizy matematyczne ważne dla metod numerycznych.
Granica (jeśli istnieje)
![]()
oznacza
![]()
, że gdy ![]()
, to ![]()
.
Ciągłość w punkcie ![]()
![]()
.
Np. funkcja
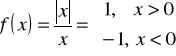
nie ma granicy i nie jest ciągła w punkcie ![]()
.
Pochodna w punkcie ![]()
![]()
jeśli istnieje, to funkcja jest ciągła w tym punkcie (odwrotnie nie jest sprawiedliwe).
Np. istnieją funkcji różniczkowalne tylko raz
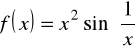
.
Wzór Taylora I.
Jeśli ![]()
i jeśli ![]()
istnieje w ![]()
, to dla ![]()
mamy
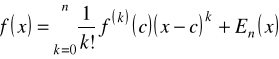
,
gdzie
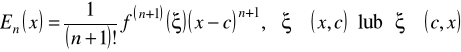
,
jest resztą Lagrange'a.
Przy ![]()
otrzymujemy wzór Maclaurina.
Przy ![]()
otrzymamy szereg Taylora (dla ![]()
— szereg Maclaurina).
Ćwiczenie. Znaleźć szeregi Taylora dla funkcji ![]()
, ![]()
, ![]()
i ![]()
.
Np. dla ![]()
przy ![]()
wzór Taylora budujemy następująco.
Pochodne
![]()
Dla ![]()
mamy
![]()
oraz
![]()
.
Więc
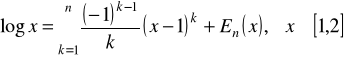
,
gdzie
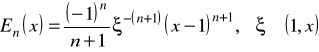
.
Ponieważ
![]()
i ![]()
,
to
![]()
.
Jest to ocena błędu przybliżenia funkcji ![]()
w punkcie ![]()
wielomianom 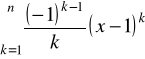
.
Np. jakie powinno być ![]()
, żeby dokładność obliczenia ![]()
była ![]()
?
Dla ![]()
mamy
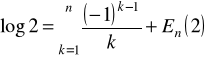
, ![]()
.
Ponieważ
![]()
, to ![]()
.
Twierdzenie Lagrange'a o wartości średniej i twierdzenie Rolle'a.
Wzór Taylora II.
Jeśli ![]()
i jeśli ![]()
istnieje w ![]()
, to dla ![]()
mamy
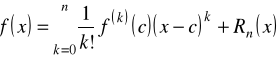
,
gdzie
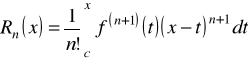
jest resztą Lagrange'a w postaci całkowej.
Wzór Taylora III.
Jeśli ![]()
i jeśli ![]()
istnieje w ![]()
, to dla ![]()
mamy
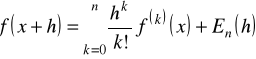
,
gdzie
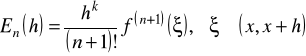
,
jest resztą Lagrange'a w tym przypadku.
Np. podać wzór Taylora dla funkcji ![]()
i obliczyć jej wartość przy ![]()
, ![]()
, ![]()
.
Ponieważ ![]()
, to
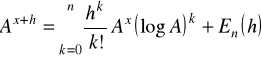
,
albo
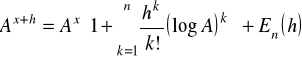
.
Zatem
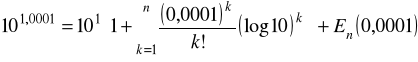
lub
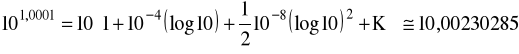
Wzór Taylora IV.
Jeśli ![]()
, to dla ![]()
mamy
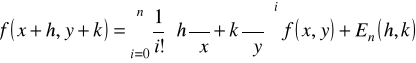
,
gdzie
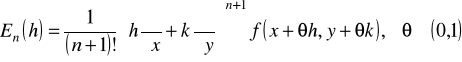
,
jest resztą Lagrange'a w tym przypadku.
Np. wyznaczyć liniową część funkcji ![]()
.
Rząd zbieżności i inne.
Program komputerowy wygenerował ciąg wyników ![]()
(![]()
), który są tylko przybliżeniem dokładnego wyniku ![]()
. Jeśli
![]()
, że gdy ![]()
, to ![]()
,
wtedy piszemy
![]()
.
Np. dla ciągu
![]()
.
Np. dla ciągu
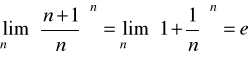
.
Ostatni ciąg wyrazów ![]()
(![]()
) jest zbieżny bardzo wolno do liczby niewymiernej ![]()
, tak ![]()
.
Ćwiczenie. Napisz kilka pierwszych wyrazów podanych ciągów.
Definicja. Mówimy o zbieżności logarytmicznej ciągu ![]()
(![]()
) do liczby ![]()
jeśli
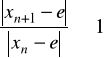
.
Definicja. Mówimy o zbieżności nadliniowej ciągu ![]()
(![]()
) zbudowanego przez wzór
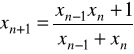
do liczby ![]()
jeśli
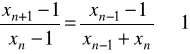
.
Definicja. Mówimy o zbieżności ciągu ![]()
(![]()
) co najmniej liniowej do liczby ![]()
jeśli
![]()
tak, że
![]()
.
Definicja. Mówimy o zbieżności ciągu ![]()
(![]()
) co najmniej nadliniowej do liczby ![]()
jeśli
![]()
tak, że
![]()
.
Definicja. Mówimy o zbieżności ciągu ![]()
(![]()
) co najmniej kwadratowej do liczby ![]()
jeśli
![]()
tak, że
![]()
.
Definicja. Mówimy o zbieżności ciągu ![]()
(![]()
) co najmniej rzędu ![]()
do liczby ![]()
jeśli
![]()
tak, że
![]()
.
Symbole ![]()
i ![]()
.
Definicja. Mówimy, że ![]()
(![]()
) jest równe „![]()
dużemu” od ![]()
(![]()
) jeśli
![]()
takie, że
![]()
i piszemy
![]()
.
Definicja. Mówimy, że ![]()
(![]()
) jest równe „![]()
małemu” od ![]()
(![]()
) jeśli
![]()
takie, że
![]()
i piszemy
![]()
.
Podobne definicji dotyczą funkcji.
Np. Rozważmy
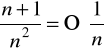
, 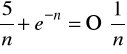
;
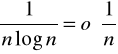
, 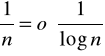
;
Twierdzenie o wartości średniej dla całek.
Funkcje uwikłane.
Równanie ![]()
nie zawsze da się rozwiązać względem poszukiwanej funkcji ![]()
. Wtedy pierwsza pochodna może być wyznaczona w następujący sposób. Różniczka zupełną funkcji ![]()
zapisuje się w postaci (![]()
, ponieważ ![]()
− stała)
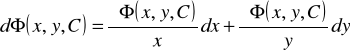
.
Przyrównując otrzymane wyrażenie do zera
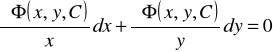
znajdziemy
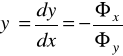
,
gdzie
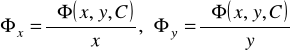
.
W podobny sposób możemy też określić pochodne wyższych rzędów.
Równania różnicowe
Załóżmy, że zbiór ![]()
złożony z ciągów nieskończonych o postaci
![]()
Określamy dwa działania
![]()
,
![]()
,
albo w skrócie
![]()
, ![]()
Zbiór ![]()
zwiera element zerowy ![]()
, elementy
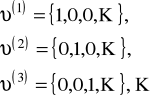
są liniowo niezależny.
Definicja. Określimy operator przesunięcia
![]()
albo
![]()
.
Operator ![]()
można stosować wielokrotnie
![]()
.
Operator identyczności, to ![]()
, tj.
![]()
.
Definicja. Poniższy operator nazywamy operatorem różnicowym
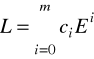
,
gdzie ![]()
(![]()
) są stałe.
Operatory różnicowe tworzą podprzestrzeń liniową z bazą ![]()
(![]()
).
Operator ![]()
jest wielomianem względem ![]()
, zatem
![]()
,
gdzie ![]()
jest wielomianem charakterystycznym operatora ![]()
, który określony wzorem
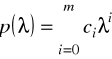
.
Wyznaczmy wszystkie rozwiązania równania różnicowego liniowego jednorodnego
![]()
.
Definicja. Jądrem operatora ![]()
nazywamy zbiór
![]()
,
który tworzę liniową podprzestrzeń.
Więc pod znajdowaniem rozwiązania możemy rozumieć określenie bazy jądra operatora.
Np. jeśli ![]()
, ![]()
, ![]()
, ![]()
, to równanie ![]()
ma postać
![]()
, (![]()
).
Zaznaczmy, że w tym przypadku możemy dowolnie wybrać wartości ![]()
i ![]()
, a wtedy wyznaczyć pozostałe.
Ogólniejsze podejście jest poszukiwanie rozwiązania równania o postaci
![]()
.
Wtedy mamy
![]()
albo ![]()
.
Pierwszy ![]()
krotny pierwiastek ![]()
odpowiada rozwiązaniu trywialnemu ![]()
. Kolejne pierwiastki ![]()
i ![]()
prowadzą do wyboru rozwiązania w postaci ![]()
i ![]()
. Więc ogólne rozwiązanie będzie
![]()
,
gdzie ![]()
i ![]()
są dowolne stałe.
Rozróżnia się pierwiastki pojedyncze i krotne oraz równania różnicowe stabilne, a także o zmiennych współczynnikach.
Przykładem równania różnicowego o zmiennych współczynnikach jest równanie rekurencyjnym dla funkcji Bessela
![]()
,
gdzie
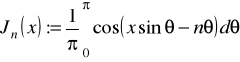
, ![]()
.
Wyszukiwarka