Elementy kinetyki chemicznej
Szybkość reakcji chemicznej
Miarą szybkości reakcji w chwili t jest zmiana liczby moli któregoś z reagentów w przedziale czasu (t, t + dt) odniesiona do jednostkowej objętości układu. Jeśli objętość pozostaje stała, odpowiada to zmianie stężenia reagenta.
Z kinetycznego punktu widzenia reakcje możemy podzielić na:
jednorodne (homogeniczne) - zachodzą w obrębie jednej fazy,
niejednorodne (heterogeniczne) - przebiegają na granicach faz,
homogeniczno - heterogeniczne (np. przebiegające na ścianach naczynia reakcyjnego).
Szybkość reakcji homogenicznej zachodzącej w stałej objętości i temperaturze definiujemy jako
![]()
(1)
gdzie ci jest chwilowym stężeniem reagenta, ![]()
jest współczynnikiem stechiometrycznym, ujemnym dla substratów, dodatnim dla produktów.
Na przykład dla reakcji
![]()
otrzymamy
![]()
(2)
Oznaczanie ci polega na przerwaniu reakcji przez obniżenie temperatury lub dodanie odpowiedniego czynnika, a następnie na wykonaniu oznaczenia dostatecznie szybką metodą fizykochemiczną (metody spektroskopii UV, IR, EPR, NMR, widma emisyjne, skręcalność optyczna, współczynnik załamania).
Rząd reakcji
Szybkość dowolnej reakcji chemicznej
αA + βB + γC + …..→ δD + εE +…..
może być ogólnie zapisana jako funkcja stężeń substratów reakcji. Doświadczalne badania zależności szybkości reakcji od stężeń wskazują, że dla wielu reakcji funkcja ta może być zapisana w postaci:
gdzie k = k(T) jest dla danego układu reagującego stałą zależną tylko od temperatury, zwaną stałą szybkości reakcji. Rzędem reakcji nazywamy wykładnik potęgowy występujący przy stężeniu substratu reakcji: mówimy, że reakcja jest rzędu α ze względu na substrat A, rzędu β ze względu na substrat B, rzędu γ ze względu na substrat C. Sumaryczny rząd reakcji jest sumą wykładników potęgowych występujących przy stężeniach substratów w równaniu kinetycznym, czyli: sumaryczny rząd reakcji = α + β + γ.
Przykłady reakcji i odpowiadające im znalezione doświadczalnie równania kinetyczne i rzędy reakcji przedstawiono poniżej.
Najczęściej reakcja chemiczna przebiega przez szereg etapów pośrednich, noszących nazwę reakcji elementarnych. Molekularnością reakcji elementarnej nazywamy liczbę cząsteczek (atomów, jonów, rodników) biorących w niej udział.
Reakcja syntezy bromowodoru: ![]()
ma złożony mechanizm, składa się bowiem z łańcucha reakcji elementarnych:
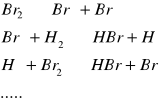
Najczęściej spotykamy się z reakcjami bimolekularnymi i monomolekularnymi; reakcje trójcząsteczkowe są bardzo rzadkie.
Podstawowe równania szybkości rekcji
Reakcje I rzędu
Rozważmy reakcję I rzędu: ![]()
, której szybkość można zapisać jako
![]()
(4)
(W ogólnym równaniu na szybkość reakcji ![]()
podstawiamy ![]()
)
Szybkość reakcji jest proporcjonalna do chwilowego stężenia ![]()
substratu A:
![]()
(5)
Jeśli szybkość reakcji będziemy mierzyć jako ubytek stężenia substratu A, to możemy napisać, że
![]()
(6)
Jeśli oznaczmy stężenie początkowe substratu A jako a, zaś stężenia A po czasie t jako równe ![]()
, to porównując prawe strony równań (4) i (5) otrzymamy następujące równanie różniczkowe:
![]()
(7)
które całkujemy rozdzielając uprzednio zmienne:
![]()
(8)
Całkowanie prowadzimy w granicach od a do ![]()
oraz od 0 do t.
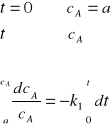
(9)
Rozwiązania tego równania przedstawiają wyrażenia
![]()
(10)
lub
![]()
(11)
![]()
(12)
Równanie (12) daje możliwość obliczenia stężenia substratu A po dowolnym czasie t.
Na podstawie równania (10) możemy wyznaczyć tak zwany czas połowicznej przemiany, ![]()
,
czyli czas, po którym stężenie substratu spadnie do połowy wartości początkowej (a/2):
Wykresy równań (10) lub (11) pozwalają na wyznaczenie stałej szybkości reakcji jako wartości współczynnika kierunkowego prostych:
Jeśli interesuje nas zależność stężenia produktu B od czasu, to równanie na szybkość reakcji zapiszemy nieco inaczej. Załóżmy, że po czasie t reakcji ulega x moli/dm3 substratu A. W układzie pozostanie, zatem (a - x) moli substratu A, powstanie zaś x moli/dm3 produktu B. Szybkość tworzenia produktu B zapiszemy jako
![]()
bowiem ![]()
. (14)
Wiemy również, że szybkość tworzenia B jest proporcjonalna do chwilowego stężenia substratu A, czyli do (a-x).
Szybkość reakcji możemy, więc wyrazić równaniem
v = ![]()
(15)
Porównując prawe strony równań (14) i (15) otrzymujemy
![]()
(16)
Równanie (14) zapisujemy jako
![]()
(17)
i całkujemy w granicach:
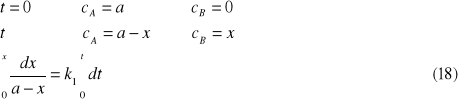
Aby rozwiązać powyższe równanie stosujemy metodę podstawiania:
a - x = z, - dx = dz

![]()
(20)
Rozwiązanie tego równania można przedstawić w postaci:
Ażeby graficznie wyznaczyć stałą szybkości należy narysować wykres zależności
![]()
Wartość stałej szybkości reakcji będzie równa wartości współczynnika kierunkowego tej prostej.
Do reakcji I rzędu zaliczamy:
elementarne reakcje jednocząsteczkowe,
reakcje dwucząsteczkowe przebiegające przy dużym nadmiarze jednego z reagentów,
reakcje złożone z kilku reakcji elementarnych, z których najwolniejsza jest reakcja jednocząsteczkowa.
Reakcje drugiego rzędu
Rozważmy reakcję
A + B →C + D
Jeśli szybkość takiej reakcji opisywana jest równaniem
![]()
oraz jeśli stężenia początkowe substratów A i B są równe odpowiednio a i b oraz a = b, to dla czasu t = 0 cA = a, cB = a, cC = 0 cD = 0
to równanie (22) można zapisać następująco:
![]()
(23)
Po rozdzieleniu zmiennych i scałkowaniu otrzymamy
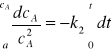
![]()
(24)
Z równania (24) wynika, że wykres zależności 1/ca od t jest linią prostą o nachyleniu równym stałej szybkości.
Na podstawie równania (24) możemy obliczyć czas połowicznej przemiany:
Jeśli interesuje nas szybkość tworzenia produktów reakcji, to zakładając, że po dowolnym czasie t tworzy się x moli/dm3 produktów otrzymamy możemy napisać, że dla
t = 0 cA = a, cB = a, cC = 0 cD = 0
t = t cA = a - x cB = a - x cC = x cD = x
Przy tych założeniach szybkość tworzenia produktu C lub D będzie równa
Rozwiązanie tego równania (metodą podstawiania: (a-x) = z) daje w wyniku równanie
![]()
a stałą szybkości można wyznaczyć jako współczynnik kierunkowy prostej z wykresu
Jeśli a ≠ b, to przy przyjętym schemacie reakcji A + B →C + D
t = 0 cA = a cB = b cc = 0 cD = 0
t = t cA = a - x cB = b - x cc = x cD = x
Rozwiązanie tego równania metodą rozkładu na ułamki proste daje
![]()
(26)
Aby wyznaczyć stałą szybkości należy sporządzić wykres zależności ![]()
.
Reakcje III rzędu
Rozważmy reakcję typu A + B + C → produkty
Jeśli stężenia początkowe substratów są jednakowe, to
Rozwiązanie powyższych równań prowadzi do zależności:
Aby wyznaczyć stałą szybkości należy sporządzić wykres zależności
![]()
.
Podobnie jak dla reakcji II rzędu można wykazać, że czas połowicznej przemiany dany jest wyrażeniem:
![]()
(31)
Reakcje zerowego rzędu
A→ produkt B
Szybkość reakcji zerowego rzędu jest stała, niezależna od stężeń substratów.
Rozważania kinetyczne prowadzą do następujących zależności:
Reakcje n-tego rzędu
Można udowodnić, że jeśli stężenia początkowe substratów są jednakowe i równe a, to słuszne są następujące zależności:
Metody wyznaczanie rzędu reakcji
Najłatwiej jest wyznaczyć rząd reakcji metodą graficzną. Wykorzystujemy fakt, że dla reakcji określonego rzędu odpowiednia funkcja stężenia jest liniowo zależna od czasu. Wykreślając kolejno zależności c - t, lnc - t, 1/c - t, 1/c2 - t itd., sprawdzamy, czy reakcja jest rzędu 0, I, II, czy n-tego rzędu.
Rząd reakcji można też wyznaczyć wyznaczając czas połowicznej przemiany dla różnych stężeń początkowych substratu. Jak już wspomniano wcześniej, jeśli szybkość danej reakcji można opisać równaniem typu
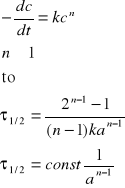
Logarytmując obustronnie ostatnie równanie otrzymujemy
![]()
(35)
Wykres zależności ![]()
od lna jest linią prostą malejącą, a jej współczynnik kierunkowy daje nam wartość (1-n).
Zależność stałej szybkości od temperatury
Zależność stałej szybkości reakcji od temperatury podaje równanie Arrheniusa,
![]()
(36)
które można zapisać w postaci
![]()
(37)
gdzie: A - stała całkowania (czynnik częstości, czynnik przedwykładniczy),
Ea - energia aktywacji: najmniejsza energia, jaką muszą mieć (w przeliczeniu na 1 mol) cząsteczki substratów, aby mogły wejść w daną reakcję,
![]()
(czynnik Boltzmanna) - ułamek drobin, które osiągnęły minimalną energię potrzebną, aby zaszła reakcja.
Równanie Arrheniusa jest spełnione w przypadku reakcji elementarnych.
2
![]()
a
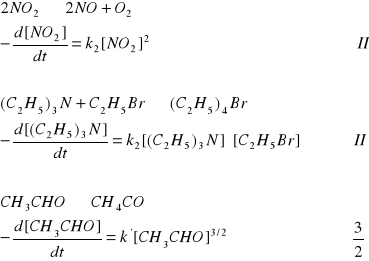
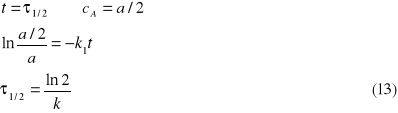
t

![]()
![]()
![]()
t


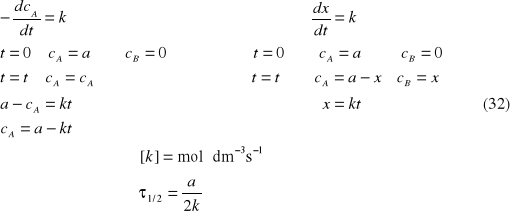
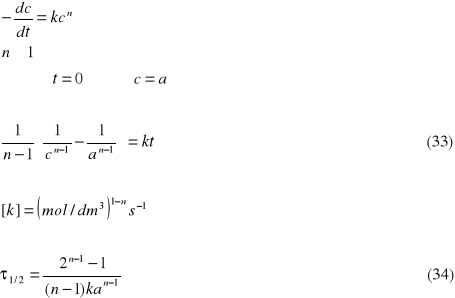
t
ln cA
ln a
cA
t
t
![]()
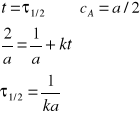
![]()
t
![]()
![]()
![]()
t
Wyszukiwarka