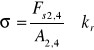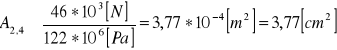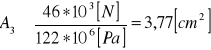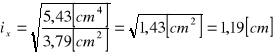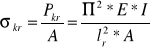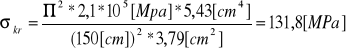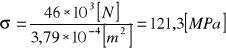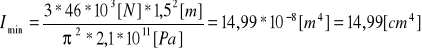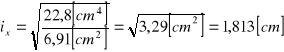Dane	Obliczenia	Wyniki
P = 22 [kN] l = 1 [m] p = 11 - ilość prętów w = 7 - ilość węzłów Dla Stali St3S Re = 220 [Mpa] xE = 1,8	Wyznaczanie reakcji w podporach RB = 22 [kN] RI = 22 [kN] Sprawdzanie statycznej wyznaczalności kratownicy 11=11 Wyznaczanie sił w prętach metodą Cremony Na podstawie załączonego rysunku poszczególne siły mają wartość (znak minus oznacza siłę ściskającą): Fs1= -13 [kN] Fs2= 26 [kN] Fs3= - 26 [kN] Fs4= 26 [kN] Fs5= 0 [kN] Fs6= - 26 [kN] Fs7= 0 [kN] Fs8= 26 [kN] Fs9= - 26 [kN] Fs10= - 13 [kN] Fs11= 26 [kN] Obliczenia wytrzymałościowe węzła II	RB = 22 [kN] RA = 22 [kN] Kratownica jest statycznie wyznaczalna.

Dane	Obliczenia	Wyniki
Fs2,4= 46 [kN] Fs3 =- 46 [kN] l = 1,5 [m] α = 1 A3= 3,79 [cm^2] E = 2,1*10^5[Mpa] Dla stali St3S	obliczanie przekroju pręta 2 i 4 korzystając z warunku na rozciąganie przyjęto kątownik o polu powierzchni przekroju A2,4 = 3,79[cm^2] obliczanie przekroju pręta 3, uwzględniając wyboczenie korzystając z warunku na ściskanie przyjęto ten sam kątownik o polu powierzchni przekroju A3= 3,79 [cm^2] uwzględniając wyboczenie dla kątownika główne centralne momenty bezwładności wynoszą: promienie bezwładności przekroju: smukłość pręta: ponieważ wyboczenie jest sprężyste naprężenia krytyczne wyznaczono korzystając ze wzoru Eulera:	A2,4 = 2,13[cm^2]
Dla kątownika 60x60x6 I = 22,8[cm^4] A=6,91[cm^2] a = 336[MPa] b = 1,48[MPa]	naprężenia ściskające pręt: rzeczywisty współczynnik bezpieczeństwa: n<nw kątownik ulega wyboczeniu obliczam minimalny moment bezwładności kątownika z warunku na wyboczenie zakładając że jest ono sprężyste Przyjmuje kątownik 60x60x6 Obliczam smukłość pręta 3 lr= α*l=1*1,5=1,5 [m] wiec wyboczenie jest posprężyste. Nie można korzystać ze wzoru Eulera. Należy powtórzyć obliczenia posługując się wzorem Tetmajera-Jasińskiego. naprężenia ściskające pręt: Rzeczywisty współczynnik bezpieczeństwa: n>nw Kątownik 60x60x6 nie ulegnie wyboczeniu poddany ściskaniu siłą 46 kN

Dane	Obliczenia	Wyniki
Dane	Obliczenia	Wyniki
kr = 110 [MPa] z = 1 z0 = 0,65 Fs2,4= 46 [kN] g = 5 [mm] h = 40 [mm] e = 11,6 [mm] g = 6 [mm] Fs3= - 46 [kN] h = 60 [mm] e = 16,9 [mm]	Obliczanie długości spoin łączących kątowniki z blachą węzłową , dla spoin przyjmuje Xe=2 dla prętów 2 i 4 rozciąganych wykonanych z kątowników , gdzie As oznacza powierzchnię spoiny rzeczywiste wymiary spoin (uwzględniając powstawanie kraterów) dla pręta 3 ściskanego wykonanego z kątownika , gdzie As oznacza powierzchnię spoiny rzeczywiste wymiary spoin (uwzględniając powstawanie kraterów)
gmax = 6 [mm]	Dobór blachy węzłowej gbw - grubość blachy węzłowej gmax - grubość największego elementu wymiary i kształt blachy wg rysunku

1

h

f

e

l_e

l_f

P

h

f

e

l_e

l_f

P

---