Zadania na ćw. nr 5. Przenikanie

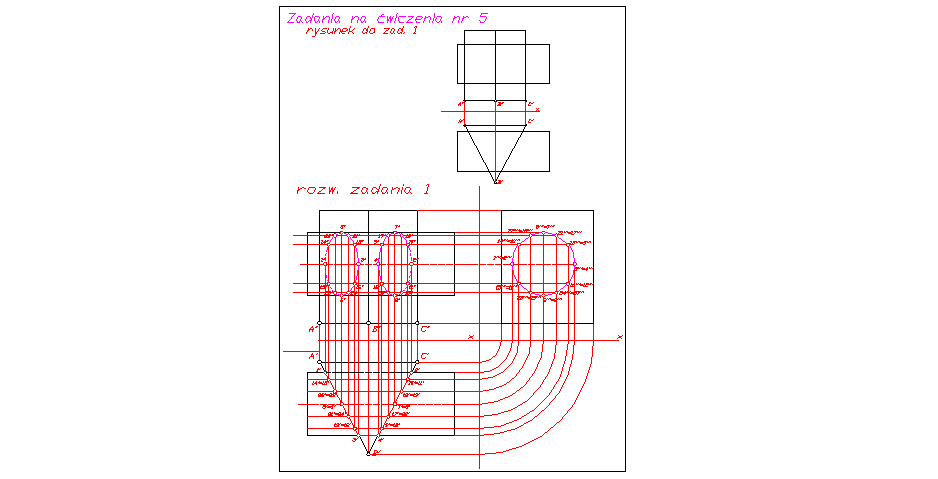
Zad. 1. Wyznacz linię przenikania graniastosłupa trójkątnego z powierzchnią walca.

Rozw.

Rozwiązanie polega na wyznaczeniu parunastu punktów przebicia tworzącymi walca powierzchni wielościanu (im więcej tych tworzących tym większa dokładność wyznaczanej linii przenikania) Zadanie to rozwiązano przy pomocy trzeciej rzutni

Patrz rys. 1.

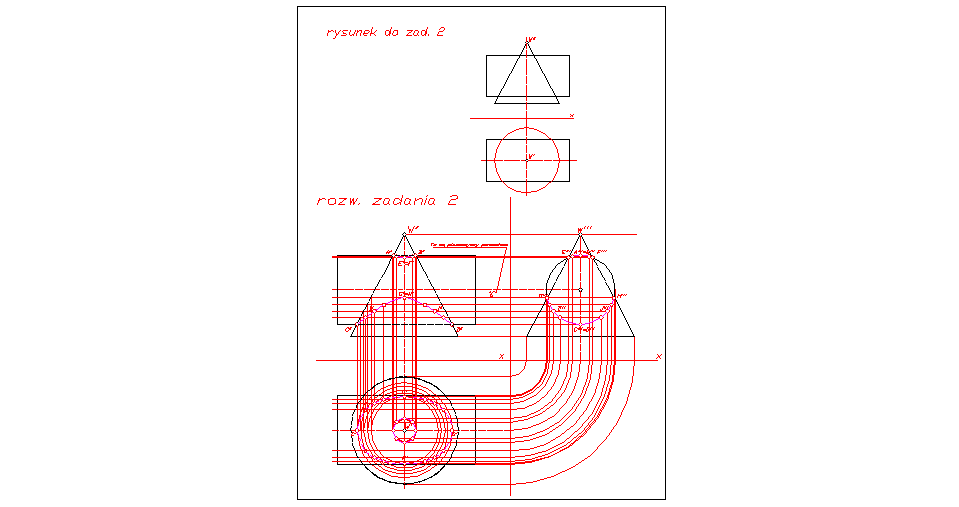
Zad. 2. Wyznacz linię przenikania powierzchni walcowej z powierzchnią stożkową.

Rozw.

Również w tym zadaniu wykorzystujemy trzecią rzutnię. Płaszczyzny pomocnicze pozwalają wyznaczyć części wspólne w postaci punktów przekrojów powierzchni walcowej (tworzących) i przekrojów powierzchni stożkowych (okręgów), wyznaczając linię przenikania.

Patrz rys. 2.

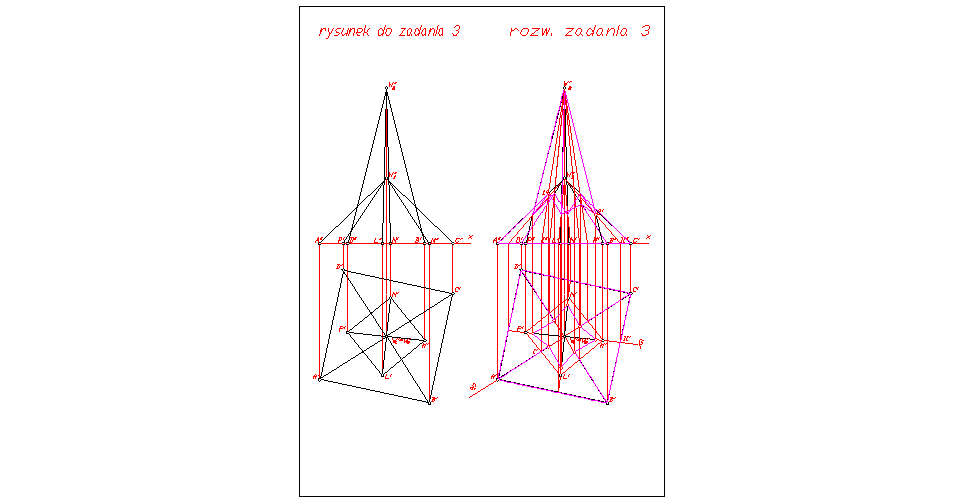
Zad. 3. Wyznacz linię przenikania pobocznic dwóch prawidłowych czworościennych ostrosłupów.

Rozw.

Prosta łącząca wierzchołki obu ostrosłupów jest pionowa, wobec czego płaszczyzny pomocnicze tworzą pęk płaszczyzn poziomo - rzutujących. Np. wybierzmy z nich tę, która przechodzi przez prostą W₁A=α; jest to płaszczyzna α, która przecina wyższy ostrosłup w trójkącie. Prosta a przecina bok IW₂ tego trójkąta w punkcie 1 wielokąta przenikania. Podobnie płaszczyzna β przechodząca przez prostą W₂M=m przecina niższy ostrosłup w trójkącie, którego bok IIW₁ przecina prosta m w punkcie 2. Tę operację wprowadzania płaszczyzn należy powtarzać kilkakrotnie, jednakże nie wprowadzono oznaczeń pozostałych płaszczyzn dla większej czytelności rysunku.

Przypominam Państwu o kolokwium zaliczeniowym, które odbędzie się na kolejnym spotkaniu.

---