Adam Mizera środa, 01 marca 2000

I rok fizyki

Ćwiczenie nr 9

WYZNACZANIE MODUŁU YOUNGA

METODĄ JEDNOSTRONNEGO ROZCIĄGANIA

Lp.	długość drutu [m]	Średnica drutu [mm]
1	0,918	0,81
2	0,919	0,81
3	0,919	0,81
4	0,918	0,81
5	0,918	0,81

Lp.	Średnica wskaz. [mm]	Il. działek na skali
1	0,99	16

Lp.	Masa	Wydłużenie	Wydłużenie
1	1	3	7
2	2	8	10
3	3	12	13
4	4	15	17
5	5	18	19
6	6	20	21
7	6,5	21	21

Zagadnienia teoretyczne.

Jeśli na jakieś nieruchome ciało wywierana jest siła, to znaczy jeśli doznaje ono pewnego ciśnienia p, to w ciele tym występują odkształcenia, czyli deformacje. Deformacje mogą być związane ze zmianami objętości ciała - mówimy wtedy o odkształceniach objętościowych - lub też ze zmianami kształtu ciała - mówimy wtedy o odkształceniach postaci. W praktyce zwykle jeden rodzaj odkształcenia występuje obok drugiego, przy czym może się zaznaczyć wyraźna przewaga jednego z nich, co w rozważaniach przybliżonych upoważnia do zaniedbania drugiego.

Odkształcająca ciało siła zewnętrzna powoduje zmianę odległości międzycząsteczkowych. Tej zmianie przeciwstawiają się siły międzycząsteczkowe ciała, dzięki którym powstaje tzw. opór sprężysty albo siła sprężystości; siła ta jest skierowana przeciwnie względem siły odkształcającej, a co do wartości jest jej równa. Siła oporu sprężystego jest tym większa, im większe jest odkształcenie; rośnie ona liniowo wraz z odkształceniem. Ilościowo ujmuje tę zależność prawo Hooke'a, które wyraża się równaniem:

;

α oznacza tu odkształcenie względne, p ciśnienie, k- jest to współczynnik proporcjonalności zwany modułem sprężystości, który ma dla danego materiału wartość stałą zależną od rodzaju odkształcenia. Z chwilą gdy ustaje działanie zewnętrznej siły odkształcającej, ciało powraca do pierwotnego stanu; siły napięć sprężystych, które powstały we wnętrzu ciała, sprawiają, że cząsteczki powracają do pierwotnych położeń. Oczywiście następuje to tylko wówczas, gdy siła odkształcająca nie przekracza pewnej granicy, tzw. sprężystości, w przeciwnym bowiem razie doznane odkształcenia ciała nie ustępują z chwilą zniknięcia siły zewnętrznej. Takie odkształcenia nazywamy plastycznymi. Prawo Hooke'a jest słuszne jedynie w odniesieniu do odkształceń sprężystych, a więc znikających wraz z działaniem siły zewnętrznej.

Zależnie od rodzaju odkształcenia mamy dla danego materiału różne moduły sprężystości: przy odkształceniu postaci polegającym na rozciąganiu względnie kurczeniu pręta występuje moduł wydłużenia, przy skręcaniu pręta mamy moduł skręcenia itp. Każdy moduł sprężystości wyraża się w jednostkach ciśnienia, tzn. N/m². Z pierwszego wzoru wynika bowiem, że moduł sprężystości określa stosunek

.

Odkształcenie względne α wyraża się stosunkiem odkształcenia względnego do początkowych wymiarów ciała i jest wobec tego liczbą oderwaną.

Największe znaczenie praktyczne ma moduł sprężystości na wydłużenie. Nosi on nazwę modułu Younga i oznaczany jest symbolem E. Na podstawie powyższego wzoru moduł Younga

.

Z wyrażenia tego łatwo można odczytać sens fizyczny modułu Younga: jest to takie ciśnienie, które spowodowałoby odkształcenie względne równe jedności. Moduł Younga jest jedynie pewną stałą, mającą orientować o wielkości sił sprężystym w danym ciele.

Śruba mikrometryczna lub - krótko - mikrometr pozwala mierzyć wymiary liniowe z dużą dokładnością, mianowicie do 0,01 mm. Mikrometr taki składa się ze śruby i nieruchomego ramienia, pomiędzy którymi umieszczamy mierzony przedmiot. Obwód bębna podzielony jest na 50 lub 100 części: skok śruby odpowiednio 0.5 mm lub 1 mm. W przypadku gdy skok wynosi 0,5 mm i bęben podzielony jest na 50 części, należy pamiętać, że skala główna jest wykreślona z dokładnością do 0,5 mm. Pięćdziesiąte części odczytane na bębnie należy dodać do wyniku.

Obliczenia:

Do obliczenia modułu Younga dla poszczególnych obciążeń wykorzystamy przekształcenie wzoru na
(wstęp teoretyczny):

.

Poziom 0 na podziałce (przy naciągniętym drucie
[m]) dla 30 jednostek. Długość jednej działki wyznaczamy ze stosunku średnicy wskazówki (0,99 [mm] - zmierzone śrubą mikrometryczną) do ilości podziałek jaką zajmowała wskazówka na skali mikroskopu odczytowego (16):
[mm] = 0,00006 [m].

Pozostałe dane:

[mm] = 0,00081 [m], czyli
[m];

.

Uwaga: Warto zauważyć, że promień drutu nie był mierzony bezpośrednio, a jedynie wyznaczony z wielkości średnicy. Wykorzystanie tak obliczonego promienia nie ma jednak większego wpływu na błąd wyników.

Obliczenia 1 (dokładanie odważników):

Dla 1 kilograma - rozciągnięcie 3 działki tj.
[m]

Dla 2 kilogramów - rozciągnięcie 8 działek tj.
[m]

Dla 3 kilogramów - rozciągnięcie 12 działki tj.
[m]

Dla 4 kilogramów - rozciągnięcie 15 działek tj.
[m]

Dla 5 kilogramów - rozciągnięcie 18 działki tj.
[m]

Dla 6 kilogramów - rozciągnięcie 20 działki tj.
[m]

Dla 6,5 kilograma - rozciągnięcie 21 działek tj.
[m]

Obliczenia 2 (zabieranie odważników):

Dla 6 kilogramów - rozciągnięcie 21 działek tj.
[m]

Dla 5 kilogramów - rozciągnięcie 19 działek tj.
[m]

Dla 4 kilogramów - rozciągnięcie 17 działek tj.
[m]

Dla 3 kilogramów - rozciągnięcie 13 działek tj.
[m]

Dla 2 kilogramów - rozciągnięcie 10 działki tj.
[m]

Dla 1 kilograma - rozciągnięcie 7 działki tj.
[m]

Obliczenie wartości średniej modułu Younga:

9,706+7,279+7,279+7,765+8,088+8,735+9,012+8,319+7,662+6,851+6,719+5,823+4,159 =97,4

Rachunek błędu:

Wykonujemy metodą różniczki zupełnej.

;
.

Dla wygody L to długość drutu początkowa, zaś l to przyrost długości (rozciągnięcie).

;
;
.

Błędy pomiarowe:

;
(pół podziałki);
.

Błąd można policzyć dla każdego pomiaru i uśrednić.

Rachunek błędu (dokładanie odważników):

Dla 1 kilograma:

=

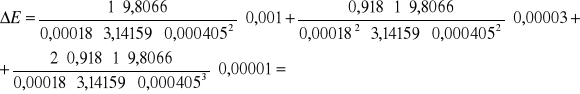
Dla 2 kilogramów:

ΔE = 0,822 10¹⁰

Dla 3 kilogramów:

ΔE = 0,671 10¹⁰

Dla 4 kilogramów:

ΔE = 0,651 10¹⁰

Dla 5 kilogramów:

ΔE = 0,633 10¹⁰

Dla 6 kilogramów:

ΔE = 0,659 10¹⁰

Dla 6,5 kilograma:

ΔE = 0,669 10¹⁰

Rachunek błędu (zabieranie odważników):

Dla 6 kilogramów:

ΔE = 0,618 10¹⁰

Dla 5 kilogramów:

ΔE = 0,588 10¹⁰

Dla 4 kilogramów:

ΔE = 0,547 10¹⁰

Dla 3 kilogramów:

ΔE = 0,598 10¹⁰

Dla 2 kilogramów:

ΔE = 0,585 10¹⁰

Dla 1 kilograma:

ΔE = 0,507 10¹⁰

Błąd średni modułu Younga:

2,107+0,822+0,671+0,651+0,633+0,659+0,669+0,618+0,588+0,547+0,598+0,585+0,507= =9,656

Błąd względny:
.

Wnioski:

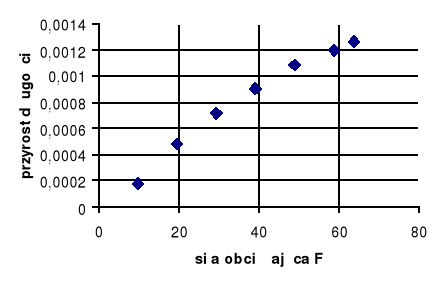
Jak widać z wykresu zależności wydłużenia od działającej siły, prawo Hooke'a jest zachowane dla „dokładania odważników” (z pewnymi założeniami, o których dalej). Dla „zabierania odważników” widać duże odstępstwa - rozkład wartości nie leży wzdłuż jednej prostej. Najprawdopodobniej jest to związane z tym, że po zmniejszeniu ciężaru drut nie skraca się momentalnie a dopiero po krótkim czasie. Inną przyczyną niedokładności rozkładu wartości (zarówno przy zwiększaniu jak i zmniejszaniu ciężaru) jest sam sposób prowadzenia pomiaru. Sam przyrząd imponuje swoją dokładnością jednak najmniejsze drgnięcie mikroskopu odczytowego powoduje skok na skali - nawet do 5 działek!

Powyższe fakty mają też wpływ na rozbieżność średniej wartości modułu Younga (ze wszystkich ciężarków) i wartości modułu policzonej z nachylenia prostej. Wykres jest wykonany dla przebiegu idealnego rozciągania drutu (prawo Hooke'a), gdyż należało uwzględnić wyżej wspomniane niedokładności - dla takich małych odkształceń można pominąć odchylenia od prawa Hooke'a.

Ciekawe jest też to, że mimo tak dużej dokładności pomiaru wydłużenia i średnicy drutu (mikroskop i śruba mikrometryczna), składniki różniczki zawierające owe dokładności mają główny wpływ na wielkość błędu. Błąd pomiaru długości początkowej drutu miarką milimetrową praktycznie nie ma wpływu.

---