Rys.1
1. Wstęp.
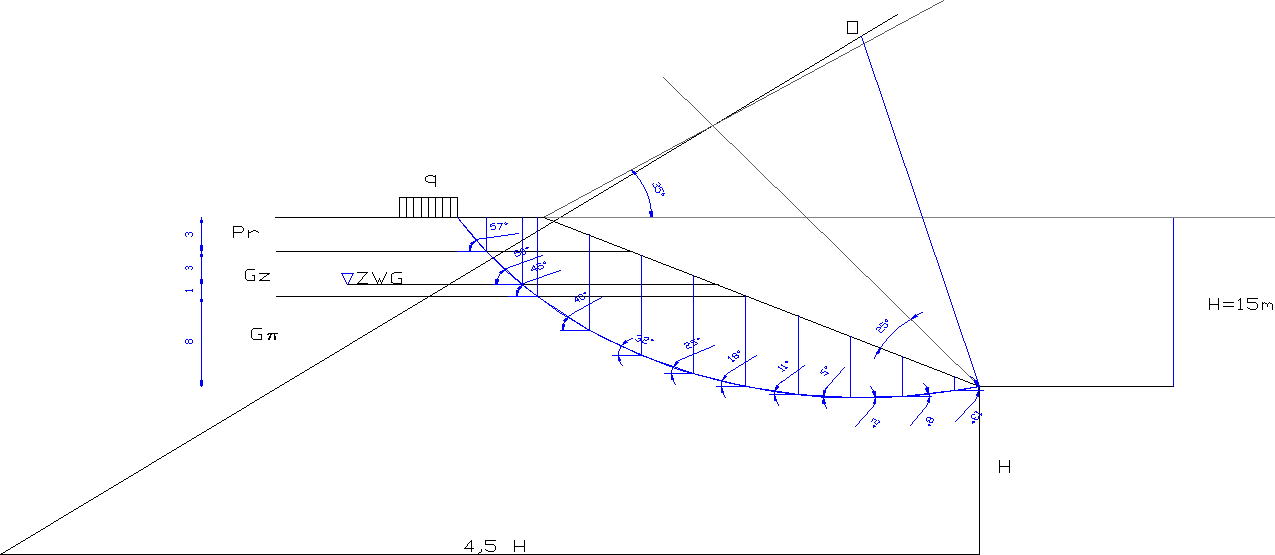
Dla zadanych warunków gruntowych sprawdzić stateczność skarpy gruntowej o nachyleniu 1:2 metodą Felleniusa przy zadanym obciążeniu q = 0,14 MPa. Obliczenia dokonane są sposobem normowym wg PN-81/B 03020 - Grunty budowlane. Posadowienie bezpośrednie budowli na gruncie. Obliczenia statyczne i projektowanie.
2. Opis obiektu
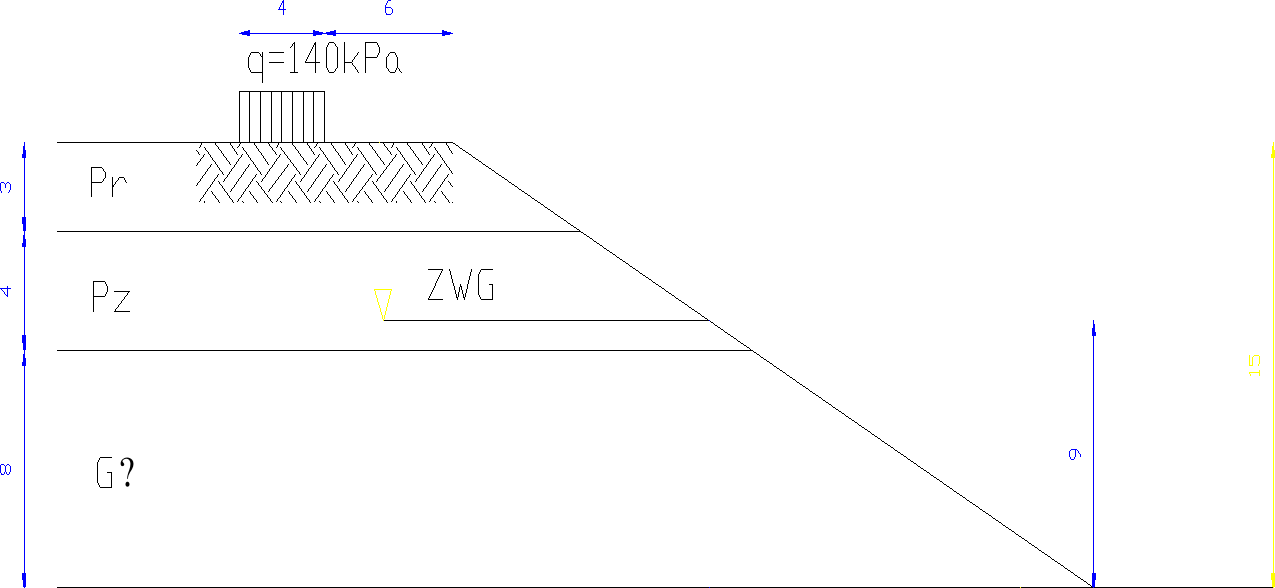
Sprawdzanym obiektem jest skarpa zbiornika wodnego, zalewu położonego w Przewornie. Skarpa ma wysokość 15 m oraz nachylenie 1:2 .Zwierciadło wody gruntowej znajduje się na wysokości 9 m od dolnej krawędzi skarpy. Skarpa nie jest uszczelniona i woda wnika w głąb skarpy. W odległości 6 m od górnej krawędzi skarpy znajduje się budynek „Wypożyczalni sprzętu wodnego”, który na długości 4 m przekazuje obciążenie równomiernie rozłożone na grunt o wielkości q=0,14 Mpa.
3. Charakterystyka geotechniczna podłoża
W trakcie badań polowych wykonanych metoda sondowania dynamicznego (końcówka cylindryczna, oraz na podstawie badań laboratoryjnych ustalono, iż badana skarpa składa się z trzech warstw. Pierwszą z nich licząc od naziąbu jest piasek gruby o miąższości 3 m o ID = 0,7. Druga to Glina zwięzła o miąższości 4 m , o IC = 0,7. Następna warstwą jest glina pylasta o Ic = 0,5.
W skarpie znajduje się ZWG na wysokości 9m, licząc od krawędzi dolnej skarpy.
Obiekt możemy zaliczyć do 2 kategorii geotechnicznej, gdyż badany skarpa wraz z budynkiem zaliczają się do złożonych warunków gruntowych.
4. Warunki gruntowe .

Rys.1
5. Ustalenie wartości obliczeniowych parametrów wydzielonych warstw:
Tabela 1a. Podstawowe cechy fizyczne |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
GRUNT |
wn [-] |
[t/m3] |
[t/m3] |
[t/m3] |
n [-] |
[t/m3] |
[kg/m3] |
[kN/m2] |
[kN/m2] |
[kN/m2] |
Pr |
0,18 |
2.05 |
2,65 |
1,74 |
0,34 |
1,08 |
1,96 |
20,11 |
10,61 |
19,26 |
Gp |
0,24 |
2.00 |
2,69 |
1,61 |
0,40 |
1,01 |
1,85 |
19,62 |
9,94 |
18,18 |
Gπ |
0,32 |
1.90 |
2,68 |
1,44 |
0,46 |
0,90 |
1,69 |
18,64 |
8,85 |
16,56 |
Tabela 1b. Parametry wytrzymałościowe |
|||
|
|
|
|
GRUNT |
|
|
|
Pr |
34 |
- |
- |
Gp |
18 |
28 |
22,95 |
Gπ |
12 |
9 |
7,38 |
![]()
Dla niespoistych c=0 i ![]()
![]()
= ![]()
(grunty spoiste).
![]()
- przyjmujemy w zależności od ![]()
=0,70.Przyjmujemy ![]()
.
6. Analiza stateczności skarpy dla kołowo-cylindrycznej powierzchni poślizgu metodą Felleniusa.
6.1. Założenia metody Felleniusa
płaski stan odkształcenia
kołowo-cylindryczna powierzchnia poślizgu
jednoczesne przemieszczenie punktów wzdłuż całej powierzchni poślizgu (klin odłamu zachowuje się jak bryła sztywna).
zakłada się brak oddziaływań między elementami (paskami) klina odłamu.
rozpatruje się tylko jeden warunek równowagi - warunek momentu dla całego klina odłamu
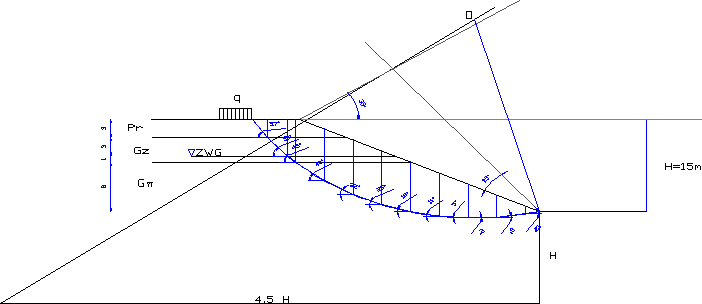
6.2. Obliczenie stateczności dla skarpy bez wody.
6.2.1 Wyznaczenie sił Wi w paskach
![]()
|
A1 |
A2a |
A2b |
A3 |
G1 |
G2a |
G2b |
G3 |
1 |
2,95 |
0 |
0,00 |
0 |
59,33 |
0,00 |
0,00 |
0,00 |
2 |
7,54 |
3,78 |
0,00 |
0 |
151,63 |
74,16 |
0,00 |
0,00 |
3 |
2,97 |
2,97 |
0,49 |
0 |
59,73 |
58,27 |
9,61 |
0,00 |
4 |
3,86 |
10,8 |
3,60 |
5,41 |
77,63 |
211,90 |
70,63 |
100,84 |
5 |
2,07 |
10,7 |
3,60 |
14,86 |
41,63 |
209,93 |
70,63 |
276,98 |
6 |
0 |
6,26 |
3,60 |
21,86 |
0,00 |
122,82 |
70,63 |
407,45 |
7 |
0 |
0,7 |
2,69 |
27,12 |
0,00 |
13,73 |
52,78 |
505,49 |
8 |
0 |
0 |
0,00 |
27,05 |
0,00 |
0,00 |
0,00 |
504,18 |
9 |
0 |
0 |
0,00 |
22,42 |
0,00 |
0,00 |
0,00 |
417,89 |
10 |
0 |
0 |
0,00 |
16,25 |
0,00 |
0,00 |
0,00 |
302,88 |
11 |
0 |
0 |
0,00 |
8,61 |
0,00 |
0,00 |
0,00 |
160,48 |
12 |
0 |
0 |
0,00 |
1,03 |
0,00 |
0,00 |
0,00 |
19,20 |
gdzie:
Gi stanowi składową ciężaru właściwego pochodzącego od każdego rodzaju gruntu w poszczególnych paskach;
![]()
Wi - wypadkowa obciążeń (sprowadzona do środka ciężkości bloku);
![]()
Bi = Wi sinα;
Ni - reakcja podłoża na składową normalną siły Wi;
Ni = Wicosαi;
Ti - opór tarcia i spójności (siła bierna, utrzymująca);
![]()
ci,φi - dla gruntu w podstawie bloku;
6.2.2. Obliczanie współczynnika stateczności F.
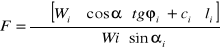
gdzie:
Wi - ciężar paska z uwzględnieniem obciążenia zewnętrznego
![]()
- kąt między powierzchnią poślizgu paska a poziomem (odczytane z rysunku);
li - szerokość powierzchni poślizgu paska (odczytane z rysunku);
![]()
- kąt tarcia wewnętrznego (odczytane z normy);
c -spójność (odczytana z normy);
nr paska |
Wi |
li |
αi |
Bi |
Ni |
Ti |
1 |
59,33 |
3,59 |
57,00 |
49,74 |
32,34 |
21,80 |
2 |
225,80 |
3,89 |
50,00 |
172,91 |
145,22 |
150,54 |
3 |
127,61 |
1,41 |
45,00 |
90,20 |
90,27 |
65,35 |
4 |
460,99 |
4,89 |
40,00 |
296,19 |
353,24 |
106,26 |
5 |
599,17 |
4,24 |
32,00 |
317,37 |
508,22 |
127,73 |
6 |
600,90 |
3,96 |
25,00 |
253,83 |
544,66 |
131,63 |
7 |
572,00 |
3,78 |
18,00 |
176,67 |
544,03 |
129,90 |
8 |
504,18 |
3,67 |
11,00 |
96,15 |
494,93 |
120,25 |
9 |
417,89 |
3,61 |
5,00 |
36,40 |
416,30 |
105,86 |
10 |
302,88 |
3,60 |
-2,00 |
-10,57 |
302,70 |
85,75 |
11 |
160,48 |
3,64 |
-8,00 |
-22,32 |
158,92 |
60,77 |
12 |
19,20 |
1,72 |
-13,00 |
-4,32 |
18,71 |
18,78 |
Przykładowe obliczenia:
![]()
![]()
G18+G28+ G'28+G38=0+0+0+504,212=504,212kN
![]()
![]()
![]()
![]()
![]()
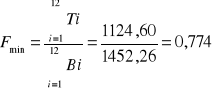
![]()
6.3. Obliczanie stateczności dla skarpy z wodą
6.3.1 Wyznaczenie sił Wi w paskach
|
A1 |
A2a |
A2b |
A3 |
G1 |
G2a |
G2b' |
G3 ' |
G2b sat |
G3 sat |
1 |
2,95 |
0 |
0,00 |
0 |
59,33 |
0,00 |
0,00 |
0,00 |
0,00 |
0,00 |
2 |
7,54 |
3,78 |
0,00 |
0 |
151,63 |
74,16 |
0,00 |
0,00 |
0,00 |
0,00 |
3 |
2,97 |
2,97 |
0,49 |
0 |
59,73 |
58,27 |
4,87 |
0,00 |
8,91 |
0,00 |
4 |
3,86 |
10,8 |
3,60 |
5,41 |
77,63 |
211,90 |
35,79 |
47,89 |
65,44 |
89,59 |
5 |
2,07 |
10,7 |
3,60 |
14,86 |
41,63 |
209,93 |
35,79 |
131,54 |
65,44 |
246,07 |
6 |
0 |
6,26 |
3,60 |
21,86 |
0,00 |
122,82 |
35,79 |
193,50 |
65,44 |
361,99 |
7 |
0 |
0,7 |
2,69 |
27,12 |
0,00 |
13,73 |
26,74 |
240,06 |
48,90 |
449,09 |
8 |
0 |
0 |
0,00 |
27,05 |
0,00 |
0,00 |
0,00 |
239,44 |
0,00 |
447,93 |
9 |
0 |
0 |
0,00 |
22,42 |
0,00 |
0,00 |
0,00 |
198,45 |
0,00 |
371,26 |
10 |
0 |
0 |
0,00 |
16,25 |
0,00 |
0,00 |
0,00 |
143,84 |
0,00 |
269,09 |
11 |
0 |
0 |
0,00 |
8,61 |
0,00 |
0,00 |
0,00 |
76,21 |
0,00 |
142,58 |
12 |
0 |
0 |
0,00 |
1,03 |
0,00 |
0,00 |
0,00 |
9,12 |
0,00 |
17,06 |
6.3.2. Obliczanie współczynnika stateczności F.
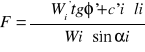
Wi |
W'i |
l |
σi |
Bi |
Ni |
Ti |
59,33 |
59,33 |
3,59 |
57,00 |
49,74 |
32,34 |
21,80 |
225,80 |
225,80 |
3,89 |
50,00 |
172,91 |
145,22 |
136,44 |
126,91 |
122,87 |
1,41 |
45,00 |
89,70 |
86,92 |
60,59 |
444,55 |
373,20 |
4,89 |
40,00 |
285,63 |
285,97 |
96,83 |
563,08 |
418,88 |
4,24 |
32,00 |
298,25 |
355,30 |
106,76 |
550,25 |
352,10 |
3,96 |
25,00 |
232,44 |
319,15 |
97,01 |
511,72 |
280,53 |
3,78 |
18,00 |
158,05 |
266,81 |
84,57 |
447,93 |
239,44 |
3,67 |
11,00 |
85,43 |
235,04 |
77,01 |
371,26 |
198,45 |
3,61 |
5,00 |
32,34 |
197,70 |
68,63 |
269,09 |
143,84 |
3,60 |
-2,00 |
-9,39 |
143,75 |
57,10 |
142,58 |
76,21 |
3,64 |
-8,00 |
-19,83 |
75,47 |
42,89 |
17,06 |
9,12 |
1,72 |
-13,00 |
-3,83 |
8,88 |
14,58 |
Przykładowe obliczenia:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
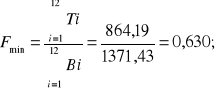
![]()
7. Wnioski
W obu rozpatrywanych przypadkach skarpę uznajemy za nie stabilna ponieważ współczynnik stateczności nie mieści się w przedziale [1,1;1,3] (za Wiłun Z., Zarys geotechniki, WKŁ, Warszawa, 1976,2001)
Zaleca się wprowadzenie środków podwyższających stateczność skarpy, np zmienieni kąta nachylenia skarpy, lub wprowadzenie kotew umacniających zbocze.