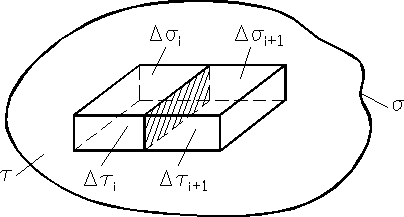
Twierdzenie Gaussa-Ostrogradskiego . Obszar o objętości τ, og-raniczony powierzchnią σ, dzielimy na podobszary o objętościach
- ograniczone powierzchniami
(rys. 12.9), przy czym

Rys. 12.9

Zgodnie z określeniem diwergencji - wzory (12.15) ÷ (12.16) - dla każdego podobszaru
możemy napisać zależności

i następnie, po ich obustronnym zsumowaniu, w granicy otrzymamy

(12.32)

gdyż strumienie wewnątrz obszaru τ ulegną redukcji ze względu na różnice w znakach strumieni wychodzących z obszaru
i wchodzących do podobszarów przyległych. Strumień wektora pola
wychodzący z powierzchni zamkniętej σ jest więc równy całce z diwergencji wektora
rozciągniętej na cały obszar τ.

W taki sam sposób możemy udowodnić twierdzenie Gaussa-Ostrogradskiego dla pola skalarnego ϕ

(12.33)

wykorzystując definicję gradientu (12.14).

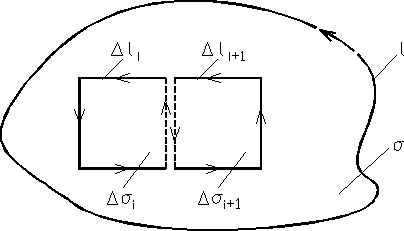
Rys. 12.10

Twierdzenie Stokesa . Powierzchnię σ ograniczoną brzegiem l wypełniamy powierzchniami elementarnymi
które są ograniczonymi liniami
(rys. 12.10)

Na podstawie definicji wirowości (12.19) ÷ (12.20), dla każdej elementarnej powierzchni
piszemy równanie

W wyniku zsumowania tych równań dla wszystkich elementów powierzchni, w granicy otrzymamy

(12.34)

ponieważ części całek elementarnych po liniach wspólnych dla sąsiednich elementów znoszą się. Cyrkulacja wektora
wzdłuż linii l  jest więc równa strumieniowi rotacji tego wektora przez dowolną powierzchnię σ, której brzegiem jest krzywa l.

12.3. Tensory kartezja*skie drugiego rz*du

Tensor. Niektóre wielkości fizyczne są bardziej złożonymi obiektami niż skalary czy wektory i muszą być określone przez więcej niż trzy składowe. Przykładem takiej wielkości fizycznej jest stan naprężenia w płynie lepkim, opisywany przez dziewięć funkcji (8.1) ÷ (8.3); naprężenie jest funkcją czasu, współrzędnych oraz orientacji powierzchni, na którą działa.

Tensor drugiego rzędu zapisuje się w postaci

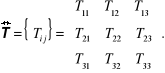
(12.35)

Skalar nazywa się niekiedy tensorem rzędu zerowego. Wektor jest tensorem rzędu pierwszego. Istnieją obiekty geometryczne i fizyczne będące tensorami jeszcze wyższych rzędów - w przestrzeni trójwymiarowej tensor rzędu n ma składowych.

Nie każda funkcja trzech współrzędnych może przedstawiać pole skalarne. Skalar musi być niezmienniczy względem zmiany układu współrzędnych, tj. przyjmować jedną i tę samą wartość w danym punkcie przestrzeni, bez względu na to w jakim układzie współrzędnych jest wyrażony. Musi więc być

(12.36)

jeśli przez
oznaczymy współrzędne x, y, z, a przez - nowy układ współrzędnych.

Po wprowadzeniu oznaczeń

(12.37)

gdzie
macierz cosinusów kierunkowych przyjmie postać

	α11	α12	α13
	α21	α22	α23	,
	α31	α32	α33

stąd

(12.38)

lub też

, (12.39)

jeśli wykorzystamy umowę sumacyjną Einsteina , oznaczającą sumowanie względem indeksu niemego j.

Podstawiając wzór (12.39) do wzoru (12.38) mamy

,

skąd wynika ortogonalność cosinusów kierunkowych

gdzie
jest tensorem jednostkowym, zwanym także delt* Kroneckera .

Podobnie nie każde trzy funkcje
przedstawiają pole wektorowe i nie każdy zbiór dziewięciu funkcji
przedstawia pole tensorowe. Wielkości 
mogą być składowymi wektora tylko wtedy, gdy transformują się jak współrzędne, tzn.:

lub
(12.40)

Również, aby wielkość fizyczna będąca tensorem nie zmieniała swojej wartości w dowolnym układzie współrzędnych, jej składowe muszą transformować się zgodnie z zależnościami

lub
(12.41)

Diada wektor*w . Rozważmy iloczyn dwu wektorów
w którym nie stosujemy żadnego z poznanych iloczynów dwu wektorów. Działając wyrażeniem
na pole wektorowe
w następujący sposób

(12.42)

w wyniku otrzymamy nowe pole wektorowe o kierunku pola
W przypadku dzia-łania
na pole
lewostronnie

(12.43)

uzyskamy pole wektorowe mające kierunek wektora
czyli

(12.44)

Operator
który odwzorowuje pole wektorowe
na inne pole wektorowe nosi nazwę iloczynu diadycznego wektor*w
i
Do jego określenia niezbędna jest znajomość dziewięciu skalarów

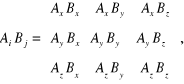
(12.45)

wynikająca z uwzględnienia cechy nieprzemienności iloczynu diadycznego

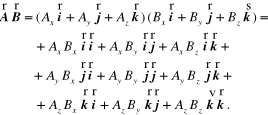
Tworząc iloczyn diadyczny 
 otrzymamy tensor, będący gradientem pola wektorowego

(12.46)

który dla wektora prędkości
zapisuje się następująco

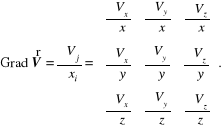
(12.47)

Zatem pochodną (3.11) można również przedstawić w postaci

(12.48)

Dla sprawdzenia, że
jest tensorem zapisujemy wielkość (12.47) w układzie

i w układzie osi obróconych

Biorąc pod uwagę wzory (12.39) i (12.40)

,

otrzymujemy zależność (12.41)

Dzia*ania na tensorach . Podstawowe działania na tensorach, nie podwyższające ich rzędu, odbywają się według następujących zasad:

1. Dodawanie

(12.49)

2. Mnożenie przez liczbę

(12.50)

3. Rozkładanie na część symetryczną
i część antysymetryczną

(12.51)

Tensor
jest symetryczny, jeżeli

(12.52)

antysymetryczny, jeżeli

(12.53)

W odróżnieniu od części symetrycznej mającej sześć składowych, część antysymetryczna ma trzy różne składowe. Część antysymetryczna przypomina więc wektor; jest ona ekwiwalentna pewnemu pseudowektorowi, będącemu np. iloczynem wektorowym dwu wektorów.

4. Iloczyn skalarny tensora i wektora (zwężenie)

(12.54)

Korzystając z tej reguły możemy np. obliczyć iloczyn występujący w pochodnej substancjalnej (12.48)

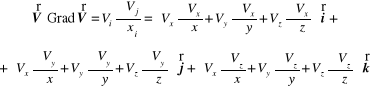
(12.55)

lub też diwergencję tensora

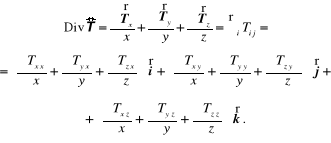
(12.56)

Przy opisywaniu ruchu lokalnego płynu (rozdz. 3.5) prędkość w dowolnym punkcie M (rys. 3.3), określonym wektorem
względem bieguna A, można wyrazić wzorem

(12.57)

w którym tensor

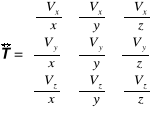
(12.58)

nosi nazwę tensora prędkości względnej .

Rozkładając tensor
na tensor symetryczny
i tensor antysymetryczny
przy zachowaniu oznaczeń (3.25), otrzymamy tensor prędkości deformacji

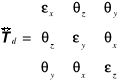
(12.59)

oraz tensor wiru

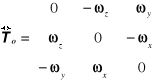
. (12.60)

W wyniku takiego rozkładu wzór (3.24) można zapisać w postaci

w której iloczyn
zawiera wyrazy w nawiasach kwadratowych, a iloczyn
- wyrazy w nawiasach okrągłych.

G**wne osie tensora . Tensor pomnożony skalarnie przez wektor, przekształca go w inny wektor, różniący się na ogół wielkością i kierunkiem. Dla dowolnego tensora można jednak znaleźć takie wektory, aby iloczyn skalarny nie zmieniał kierunku, a co najwyżej powodował zmianę ich długości lub zwrotu.

W dalszym ciągu zajmiemy się tensorami symetrycznymi o składowych spełniających związek (12.52), gdyż za pomocą tych tensorów można przedstawić wielkości tensorowe występujące w mechanice płynów. Otrzymujemy równanie

(12.61)

w którym występuje nieznany współczynnik λ. Równanie (12.61) jest równoważne układowi równań

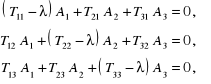
(12.62)

który posiada nietrywialne rozwiązanie ze względu na niewiadome
gdy znika wyznacznik utworzony ze współczynników układu

(12.63)

Po jego rozwinięciu otrzymujemy tzw. równanie wiekowe Laplace'a

(12.64)

w którym występują następujace wielkości :

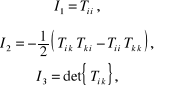
(12.65)

nie ulegające zmianie przy obrocie układu współrzędnych - są one niezmiennikami podstawowymi tensora

Pierwiastki równania wiekowego przyjmują jedynie wartości rzeczywiste. Można je obliczyć w sposób zaproponowany przez Pełczyńskiego

(12.66)

gdzie:

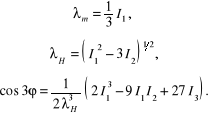
Trzem wartościom głównym
odpowiadają trzy wzajemnie ortogonalne kierunki główne, określone wektorami
których składowe otrzymuje się z układu równań (12.62). Rozważając tensor w układzie odniesienia którego osie są osiami głównymi tensora, otrzymujemy związki

gdzie wektory
o składowych
oznaczają wersory osi Dla kierunków głównych składowe normalne tensora są więc równe wartościom głównym, zaś składowe styczne znikają

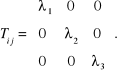
(12.67)

Dla kierunków głównych upraszcza się również większość zależności, np. mamy:

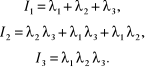
12.4. R*wnania zachowania w postaci ca*kowej

Twierdzenie Reynoldsa o transporcie . Przy obliczaniu szybkości zmian w czasie wielkości polowych w obszarze płynnym
ograniczonym powierzchnią
zachodzi potrzeba obliczania pochodnych materialnych całek

gdzie F jest funkcją określoną dla poruszającego się ośrodka, a promień
opisuje aktualne położenie elementu płynu. Korzystając z definicji pochodnej mamy

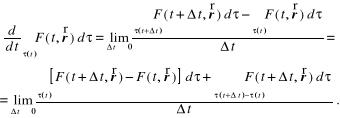
Pierwsze wyrażenie w liczniku przekształcimy rozwijając funkcję podcałkową w szereg Taylora i ograniczając się tylko do członu proporcjonalnego do

353