Szpunar Jakub 2007.03.06
I ED, gr. lab: 9/3
Sprawozdanie z ćwiczenia nr 15
Baranie rozkładu niepewności pomiarowych w pomiarach okresu wahań wahadła
1. Zagadnienia do samodzielnego opracowania
Niepewność pomiaru jest wątpliwością lub powątpiewaniem dotyczące wartości wyniku pomiaru. Definiuję się go jako parametr charakteryzujący rozrzut (odbieganie) wartości wyników, które można utożsamiać z wielkościami mierzonymi.
Niepewność można określić odchyleniem standardowym, ale powinno się brać pod uwagę wszystkie przyczyny przy rozrzucie pomiaru. Przyczynami niepewności są:
- niepełna definicja wartości mierzonej
- niedokładne wykonywanie tej definicji
- nie znajomość wpływu otoczenia lub ich niedokładny pomiar
- błędy obserwatora
- niedokładne wzorce
- przybliżenia i założenia upraszczające w pomiarach
O błędzie pomiaru można powiedzieć wtedy, gdy jest niedoskonałość w pomiarze. Tak jak w dawnej terminologii wyróżnia się 2 składniki błędu: przypadkowy i systematyczny. Błąd przypadkowy jest wynikiem nieprzewidywalnych zmian czasowych lub przestrzennych wpływających na pomiar, zwiększa on rozrzut pomiaru. Nie można go skompensować, a jego wartość wynosi zero. Błąd systematyczny jest również wynikiem czasowych lub przestrzennych zmian czynników, ale te czynniki można rozpoznać i gdy wpływ tych czynników jest duży to wprowadzić poprawkę kompensacyjną. Słowo „błąd” będzie stosowane tylko w znaczeniu błędu systematycznego
Ocena niepewności typu A
Jeżeli oceniamy, że zmienne warunki pomiaru lub zmiany mierzonego obiektu mogą powodować nieco różne wyniki decydujemy się wykonać pomiar wielokrotnie. Oznaczamy kolejne wyniki n-krotnie powtórzonego pomiaru przez xi, gdzie indeks i oznacza numer pomiaru (i=1,…,n). Wówczas średnia arytmetyczna xśr z wyników pomiarów jest dobrym oszacowaniem (estymatorem) wartości oczekiwanej
![]()
Z w/w wzoru wynika, że dla nieskończoności wielkiej liczby pomiarów średnia arytmetyczna staję się dokładnie wartością oczekiwaną. Niepewność standardowa mierzonej wielkości x utożsamiamy z odchyleniem standardowym średniej s(xśr) i tak niepewność standardowa jest opisana wzorem:
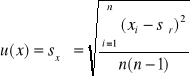
Wielkość sxśr nazywa się odchyleniem standardowym wartości średniej. Przy założeniu ze wyniki kolejnych pomiarów podlegaja rozkładowi normalnemu (Gaussa) prawdopodobieństwo znalezieniea wartości oczekiwanej µ w przedziale (xśr-µ , xśr+µ) wynosi ok. 67 %. Gdy rozkład wyników nie jest normalny, nie znamy prawdopodobieństwa i podajemy w formie dwóch wyników: xśr i µ. Miarą rozproszenia wyniów w serii pomiarowej jest odchylenie standardowe pojedynczego pomiaru sx (estymator odchylenia standardowego σ), wyraża się wzorem:
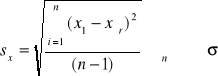
Każdą próbę można przybliżyć za pomocą jednej wspólnej krzywej, zwanej krzywą Gaussa lub krzywą gęstości rozkładu normalnego opisaną równaniem
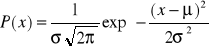
W wyrażeniu tym występują dwa parametry μ i σ, charakteryzujące mierzony obiekt;
μ oznacza wartość oczekiwaną i jest liczbą określającą położenie odciętej maksimum krzywej, a σ jest odchyleniem standardowym i charakteryzuje jej szerokość, czyli odchylenia wyników od wartości μ. Wielkość P(x) jest gęstością prawdopodobieństwa wyników pomiarowych. W przypadku, gdy pewna wielkość fizyczną mierzy się wielokrotnie, wtedy każda seria pomiarów daje się przybliżyć krzywą o tych samych parametrach μ i σ.
Z reguły jednak parametry te są początkowo nieznane. W statystyce matematycznej stosuje się funkcje zwane estymatorami, które są funkcjami zmiennych losowych.
Zalecane sposoby zapisu niepewności przedstawiamy na przykładzie. Przykład nasz wyróżnia zapis słowny (1), przy użyciu symboli (2) i skrócony (3), ale stosować można dowolną kombinację przedstawionych elementów zapisu.
Niepewność standardowa
(1) przyspieszenie ziemskie jest równe 9,866 m/s2 z niepewnością 0,028 m/s2;
(2) g = 9,866 m/s2 ; u(g) = 0,028 m/s2;
(3) g = 9,866(28) m/s2.
W doświadczeniu badamy rozkład niepewności pomiarowych przy wielokrotnym pomiarze okresu wahań wahadła matematycznego. Wahadło matematyczne jest szczególnym przypadkiem wahadła fizycznego. Wahadło to jest punktowym ciałem o masie m0 zawieszonym na cienkiej, nierozciągliwej i nieważkiej nici.
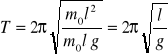
2. Wykonywanie ćwiczenia
2.1 Zmierzyć przy pomocy sekundomierza czas t pięciu wahnięć wahadła. Pomiary powtórzyć 100 razy zachowując stałą wielkość wychylenia początkowego ok. 3o, co odpowiada wychyleniu kulki o ok. 7 cm od położenia równowagi. Wyniki zapisać w tabeli:
Czas trwania pięciu okresów wahań wahadła t[s] |
|||||||||
11,875 |
11,349 |
11,401 |
11,802 |
11,663 |
11,533 |
11,575 |
11,640 |
11,404 |
11,524 |
11,949 |
11,529 |
11,316 |
11,584 |
11,533 |
11,884 |
11,644 |
11,607 |
11,492 |
11,589 |
11,639 |
11,693 |
11,635 |
11,714 |
11,610 |
11,469 |
11,483 |
11,367 |
11,643 |
11,587 |
11,376 |
11,452 |
11,704 |
11,224 |
11,749 |
11,682 |
11,501 |
11,629 |
11,612 |
11,764 |
11,630 |
11,626 |
11,712 |
11,697 |
11,421 |
11,598 |
11,529 |
11,328 |
11,386 |
11,506 |
11,801 |
11,870 |
11,833 |
11,736 |
11,298 |
11,783 |
11,573 |
11,618 |
11,573 |
11,624 |
11,811 |
11,686 |
11,610 |
11,501 |
11,376 |
11,584 |
11,647 |
11,802 |
11,649 |
11,422 |
11,653 |
11,524 |
11,810 |
11,533 |
11,678 |
11,361 |
11,632 |
11,725 |
11,510 |
11,386 |
11,469 |
11,426 |
11,427 |
11,400 |
11,621 |
11,672 |
11,833 |
11,805 |
11,561 |
11,561 |
11,423 |
11,712 |
11,820 |
11,809 |
11,724 |
11,461 |
11,538 |
11,685 |
11,575 |
11,609 |
2.2 Średnią wartość pomiarów obliczono posługując się zależnością:
![]()
tj.
![]()
2.3 Następnie obliczono odchylenie standardowe wartości średniej stśr:
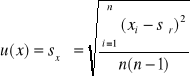
tj.
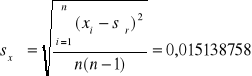
2.4 Obliczono również odchylenie standardowe pojedynczego pomiaru st:
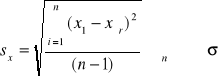
tj.
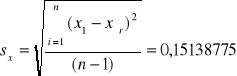
2.5 Wykres rozkładu Gaussa P(x), przyjmując, że wykonana ilośc pomiarów pozwala założyć równość: μ = xśr , σ = sx
2.6 Przedział pomiaru.
x [s] |
k/100 |
P (Δx) |
xśr - 0,5; xśr - 0,25 |
0,04 |
4 |
xśr - 0,25; xśr - 0,15 |
0,14 |
13 |
xśr - 0,15; xśr - 0,05 |
0,17 |
16 |
xśr - 0,05; xśr + 0,05 |
0,3 |
30 |
xśr + 0,05; xśr + 0,15 |
0,17 |
17 |
xśr + 0,15; xśr + 0,25 |
0,12 |
11 |
xśr + 0,25; xśr + 0,5 |
0,04 |
4 |
k - ilość pomiarów w przedziale
2.7 Histogram przedstawiający w postaci kolumn w poszczególnych przedziałach zawarte w/w tabeli.
2.8 Obliczyć okres wahań T wahadła
T = xśr / 5 = 11,59599 / 5 = 2,319198 [s]
2.9 Obliczamy okres wahań, przyjmując że wahadło jest wahadłem matematycznym.
Długość wahadła zmierzona od środka kulki wynosi (132.0 +/- 0,5cm).
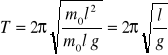
= 2,30 [s]
(∆T)max = ±![]()
. ∆l
(∆T)max = ±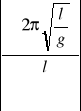
. ∆l = 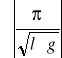
. ∆l
(∆T)max = 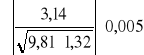
= ± 0,0044 [s]
T = 2,30 ± 0,0044 [s]
3. Wnioski
W celu zminimalizowania występowania błędów należy między innymi: każdy pomiar kilkukrotnie powtórzyć, przy czym kolejne powtórzenia nie powinny być wiernym odtworzeniem pomiaru. W kolejnych pomiarach należy zmienić możliwie najwięcej czynników, które nie powinny wpłynąć na wynik. Jeżeli to możliwe należy zmieniać stosowane przyrządy, kolejność wykonywania pomiarów, rozmieszczenie aparatury, osobę wykonującą pomiar. Gdy przedmiotem badań jest jakiś materiał, wtedy do kolejnych pomiarów należy stosować różne próbki, zmieniać ich kształt, objętość itp. Należy bardzo krytycznie sprawdzać prawidłowość zastosowanej metody pomiarów. Niekiedy można stosować różne metody pomiarów. Jeśli nie mamy wpływu na wybór metody, należy starać się oszacować błąd wnoszony przez wadliwą metodę i wprowadzić odpowiednie poprawki do wyników.
Wyszukiwarka