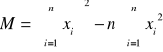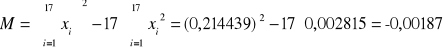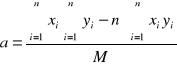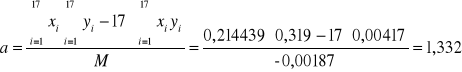Sprawozdanie z ćwiczenia nr 36.
FALOWE WŁASNOŚCI MIKROCZĄSTEK. SPRAWDZANIE HIPOTEZY DE BROGLIE'A.
Podstawowymi własnościami ruchu falowego (we wszystkich rodzajach fal) są dyfrakcja i interferencja.
Interferencja jest to nakładanie się fal o jednakowych częstotliwościach pochodzących z różnych źródeł i ma charakter konstruktywny (wzmocnienie fali) przy spotkaniu fal w fazach zgodnych lub destruktywny (osłabienie fali), gdy fale spotykają się w fazach przeciwnych.
Dyfrakcją nazywamy zmianę kierunku rozchodzenia się fali spowodowana przeszkodą ustawioną na jej drodze.
Obie te właściwości wykazuje fala elektromagnetyczna, czyli światło. Jednocześnie światło zachowuje się jak strumień cząstek zwanych fotonami. Przykładem jest efekt Comptona kiedy to foton oddziaływuje z elektronem.
Tą dwoistość natury światła pokazuje wzór:
|
łączący pęd fotonu (p) i długość fali elektromagnetycznej![]()
.
Sugeruje to, że nie tylko fotony ale również inne cząstki powinny mieć właściwości falowe. Hipotezę taką wysunął w 1924 r. de Broglie. Według niego można obliczyć długość fali materii przekształcając powyższy wzór. Oznacza to, że materia ma własności korpuskularno - falowe.
Chcąc zaobserwować falową naturę światła można zastosować tzw. siatkę dyfrakcyjną lub kryształ.
Dyfrakcja fali na krysztale polega na selektywnym wzmocnieniu fal odbitych w niektórych tylko kierunkach. Jeżeli promienie padają na kryształ w ten sposób, że tworzą z rodziną płaszczyzn sieci krystalicznej kąt ![]()
spełniający warunek Bragga i
gdzie: d - odległość między płaszczyznami atomowymi |
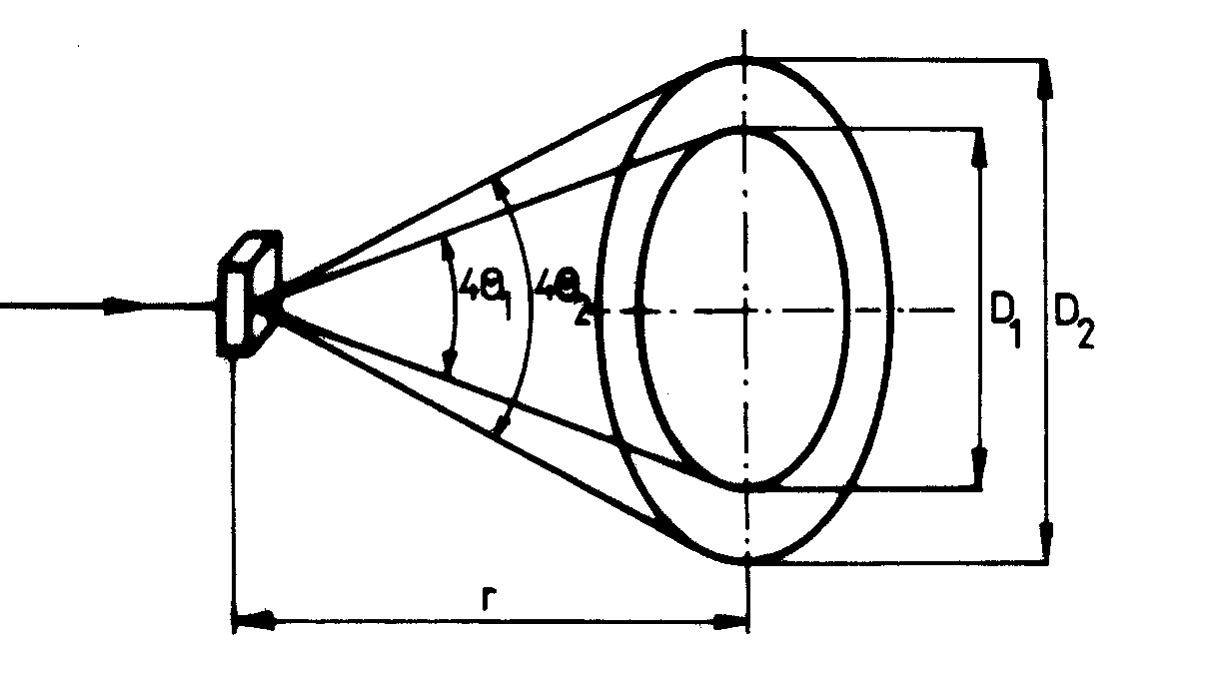
to tylko pod tym kątem zostaną wzmocnione promienie odbite, a w innych kierunkach promienie odbite spowodują efekt odwrotny (osłabienie fali). Wiązki odbite mogą tworzyć powierzchnie stożkowe o kącie rozwarcia 4![]()
jeżeli kryształ będziemy obracać względem osi pokrywającej się z kierunkiem wiązki padającej. Taki sam efekt wystąpi gdy fala pada na polikryształ.
W naszym doświadczeniu na drodze fali odbitej ustawiony jest ekran, na którym obserwujemy okręgi. Okręgi te są wynikiem interferencji fal.
Korzystając z urządzenia doświadczalnego, którego opis jest zamieszczony w instrukcji, wykonujemy pomiary średnicy wszystkich widocznych na ekranie pierścieni, zwiększając napięcie przyspieszające elektrony. Wyniki pomiarów zamieszczamy w poniższej tabeli.
|
|
|
3 |
2,9 |
4,6 |
3,5 |
2,3 |
4,4 |
4 |
2,3 |
4,4 |
4,5 |
2,2 |
3,7 |
5 |
2 |
3,5 |
5,5 |
1,9 |
3,3 |
6 |
1,8 |
3,2 |
6,5 |
1,8 |
3,2 |
7 |
1,7 |
3,1 |
7,5 |
1,7 |
3 |
8 |
1,7 |
2,9 |
8,5 |
1,7 |
2,8 |
9 |
1,6 |
2,7 |
9,5 |
1,6 |
2,7 |
10 |
1,6 |
2,6 |
10,5 |
1,6 |
2,6 |
11 |
1,5 |
2,5 |
Aby sprawdzić zgodność uzyskanych wyników z wzorem ![]()
sporządzamy wykres pierścienia ![]()
od odwrotności pierwiastka kwadratowego napięcia przyspieszającego ![]()
.

1. Korzystając z metody sumy najmniejszych kwadratów wyznaczamy wartość współczynnika nachylenia a prostej, gdzie y= ax + b ;y = D; x = ![]()
.
Korzystając z uproszczeń wyliczamy.
|
|
wówczas:
|
|
![]()
wyznaczamy przy pomocy programu Microsoft Excel funkcją zwracającą wartość sumy kwadratów odchyleń punktów danych od średniej arytmetycznej ![]()
=0,001
2. Wyznaczamy wartość odległości między płaszczyznami atomowymi d, w oparciu o wzór ![]()
r = 125mm = 0,125m;
![]()
; ![]()
; ![]()
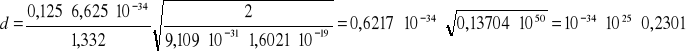
![]()
(m)
![]()
3. Tym samym sposobem, co przy pierścieniu ![]()
wyznaczamy a i d dla pierścienia ![]()
.

Wyniki dla ![]()
: a = 2,513 ; ![]()
=0,004; 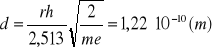
![]()
Sporządzamy tabelę zbierającą wszystkie efekty naszych pomiarów i obliczeń.
pierścień |
|
|
|
|
|
|
|
|
Wnioski:
Na podstawie otrzymanych wyników możemy potwierdzić prawdziwość hipotezy de Brogile.
- 3 -
Wyszukiwarka