KONSTRUKCJA DACHU
POZYCJA OBL. NR 1
Dane do projektowania:
konstrukcja dachu : płatwiowo-kleszczowa
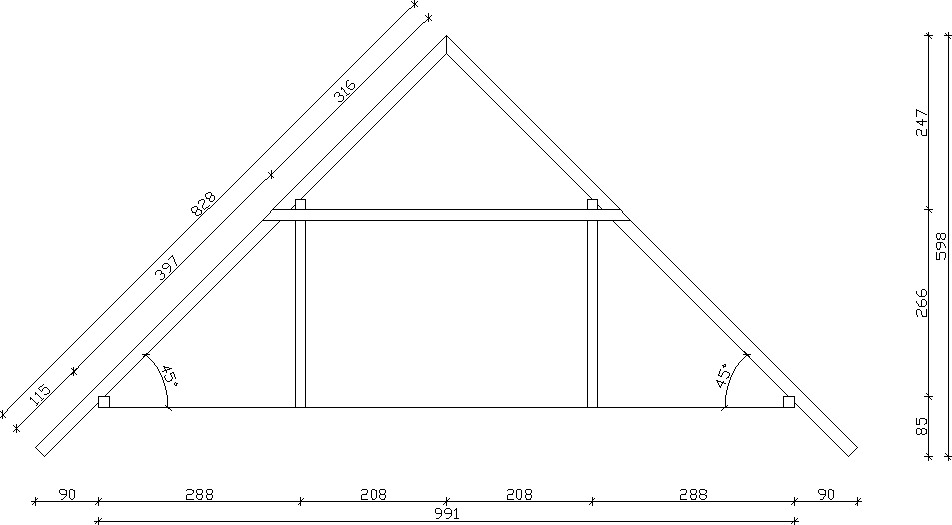
rozstaw krokwi : max. 1,24 m ; min. 0,76 m
nachylenie połaci : 45º
pokrycie dachu : dachówka ceramiczna esówka o rozstawie łat = 28 cm
lokalizacja budynku : Poznań
obciążenie śniegiem : strefa I
obciążenie wiatrem : strefa I
drewno sosnowe : klasa C30, KW gsosny = 5,5 kN/m3
dachówka - masa 1 szt. : 2,3 kg (16 szt./m2)
wysokość budynku H : 98,19 m. n.p.m
teren zabudowany przy wys. budynków do 10 m → teren B
Geometria projektowanego wiązara płatwiowo-kleszczowego:
Poz. obl. 1.1. OBLICZENIE ŁATY
Przyjęto do projektowania łaty sosnowe o wymiarach 45 x 63 mm o polu przekroju poprzecznego A = 0,002835 m2.
Obciążenia
Zestawienie obciążeń stałych g
Obciążenie |
Wartość charakterystyczna [kN/m] |
Współczynnik obciążenia γf [-] |
Wartość Obliczeniowa [kN/m] |
Ciężar własny łaty 0,002835 · 5,5 |
0,016 |
1,1 |
0,018 |
Ciężar pokrycia - waga jednej dachówki 2,3 kg, liczba - 16 szt./m2, 9,81·10-3 N/kg · 2,3 kg · 16 m-2 · 0,28 m |
0,101 |
1,2 |
0,121 |
RAZEM |
0,117 |
|
0,139 |
Obciążenie zmienne:
Wartość obciążenia śniegiem charakterystyczna Sk na 1 m2 powierzchni rzutu poziomego połaci dachowej:
Sk = Qk · C
Qk = 0,7 kN/m2 dla II strefy
Współczynniki kształtu dachy wynoszą: (dla kąta α = 45 º)
C1 = 0,8 · (( 60 - α ) / 30 ) = 0,40
C2 = 1,2 · (( 60 - α ) / 30 ) = 0,60
Dla obliczeń pojedynczych elementów przyjmuje się, że C2 = C1 = C
C = 0,40
Sk = 0,7 · 0,40 = 0,28 kN/m2
Wartość obliczeniowa obciążenia śniegiem
S = Sk · γf γf = 1,4
S = 0,28 · 1,4 = 0,392 kN/m2
Wartość obciążenia charakterystycznego wiatrem:
pk = qk · Ce · C · β
qk = 0,25 kN/m2 dla I strefy
Budynek ma wysokość z = 10,94 m < 20m , teren B
Ce = 0,8
Budynek nie jest podatny na dynamiczne działanie wiatru:
β = 1,8
Wartość współczynnika aerodynamicznego:
C=Cz
Cz = 0,015 · α - 0,2 = 0,015 · 45 - 0,2 = 0,475
lub
Cz = - 0,045 · ( 40 - α ) = -0,045 · ( 40 - 45 ) = 0,225
Przyjęto parcie dla którego:
C = 0,475
Obciążenie charakterystyczne wywołane działaniem wiatru wynosi:
pk = 0,25 · 0,8 · 0,475 · 1,8 = 0,171 kN/m2
Wartość obliczeniowa obciążenia wiatrem:
p = pk · γf γf =1,3
p = 0,171 · 1,3 = 0,222 kN/m2
Przyjęto obciążenie charakterystyczne skupione ( człowiek z narzędziami; masa = 102 kg ):
p = pk · γf pk = 1,0 kN γf =1,2
p = 1,0 · 1,2 = 1,2 kN
Przyjęto długość przęsła równą maksymalnemu rozstawowi krokwi:
leff = 1,24 m
Składowe obciążeń prostopadłe i równoległe łaty:
g┴ = g · cos α
gΙΙ = g · sin α
S┴ = S · cos2 α
SΙΙ = S · sin α · cos α
p┴ = p · Ψo Ψo = 0,9 - uwzględniono wsp. jednoczesności obciążeń
pΙΙ = 0
P┴ = P · cos α
PΙΙ = P · sin α
Zestawienie obciążeń na łatę
Obciążenie |
Wartość charaktery [kN/m] |
Wsp. obciążenia γf [-] |
Wartość obliczenio [kN/m] |
Wartości składowe prostopadłe obciążenia |
Wartości składowe równoległe obciążenia |
||
|
|
|
|
Charakter. [kN/m] |
Obliczeniowa [kN/m] |
Charakter. [kN/m] |
Obliczeniowa [kN/m] |
g- ciężar własny i pokrycia S - śnieg 0,28 · 0,28 p - wiatr 0,171 · 0,28 · 0,9 |
0,117
0,078
0,043 |
1,5
1,3 |
0,139
0,117
0,056 |
0,083
0,039
0,043 |
0,098
0,059
0,056 |
0,083
0,039
0,000 |
0,098
0,059
0,000 |
Razem |
0,238 |
|
0,312 |
0,165 |
0,213 |
0,122 |
0,157 |
P - obciążenie skupione [kN] |
1,00[kN] |
1,2 |
1,20[kN] |
0,707 |
0,849 |
0,707 |
0,849 |
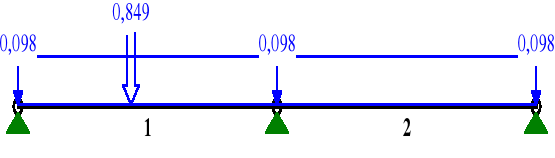
Przyjęto dwa warianty obciążeń:
wariant I (ciężar własny, ciężar pokrycia, siła skupiona)
wariant II (ciężar własny, ciężar pokrycia, obciążenie śniegiem i wiatrem )
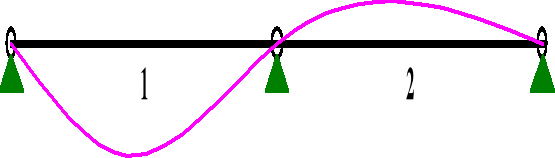
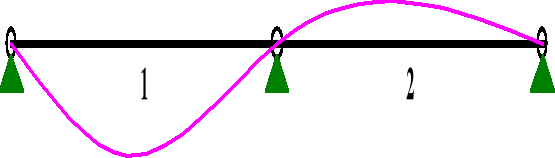
Schematy statyczne do obliczenia łaty: 1) I wariant obciążeń, 2) II wariant obciążeń:
WARIANT I
Wykresy momentów zginających wykonano za pomocą programu RM-WIN.
a) WARTOŚCI SKŁADOWE PROSTOPADŁE OBCIĄŻENIA:
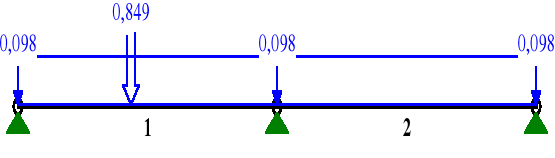
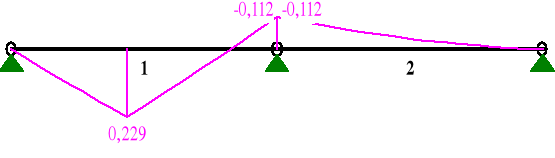
MOMENTY My:
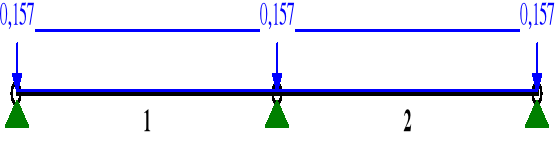
b) WARTOŚCI SKŁADOWE RÓWNOLEGŁE OBCIĄŻENIA:
MOMENTY Mz:
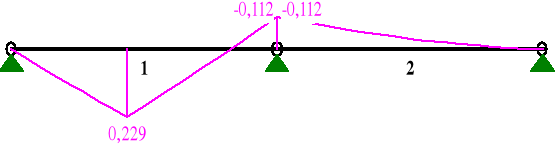
Sprawdzenie stanu granicznego nośności
Obliczenie wskaźników wytrzymałości łaty o wymiarach 45 x 63 mm:
Wy = ( 0,045 · 0,0632 ) / 6 = 29,77 · 10-6 m3
Wz = ( 0,063 · 0,0452 ) / 6 = 21,26 · 10-6 m3
Naprężenia obliczeniowe od zginania w stosunku do osi głównych wynoszą:
σm.y.d = My / Wy = 0,229 / ( 29,77 · 10-6 ) = 7692,31 kPa = 7,69 MPa
σm.z.d = Mz / Wz = 0,229 / ( 21,26 · 10-6 ) = 10771,40 kPa = 10,77 MPa
Wartość charakterystyczna drewna klasy C30 na zginanie wynosi:
f m.y.k = 30,0 MPa
Dach jest wykonany z drewna o wilgotności 12÷20 %, co określa 2 klasę użytkowania. Wytrzymałość obliczeniowa drewna na zginanie:
f m.y.d = f m.z.d = ( kmod · f m.y.k ) / γm kmod = 1,1 γm = 1,3
f m.y.d = ( 1,1 · 30,0 ) / 1,3 = 25,38 MPa
Ponieważ przekrój ma wysokość mniejszą od 150 mm stosuje się współczynnik:
kh = ( 150 / 63 )0,2 = 1,19 i jest mniejszy od 1,3
zatem:
f' m.y.d = f m.y.d · kh = 25,38 · 1,19 = 30,20 MPa
Sprawdzenie warunku sgn: ( km = 0,7 dla prostokątnych przekrojów ):
km · σm.y.d / f' m.y.d + σm.z.d / f' m.z.d = 0,7 · 7,69 / 30,20 + 10,77 / 30,20 = 0,53 ≤ 1
σm.y.d / f' m.y.d + km · σm.z.d / f' m.z.d = 7,69 / 30,20 + 0,7 · 10,77 / 30,20 = 0,50 ≤ 1
Warunek stanu granicznej nośności dla łaty został spełniony.
Sprawdzenie stanu granicznego użytkowalności
Graniczna wartość ugięcia dla deskowania dachowego wynosi:
unet,fin = leff / 150 = 1240 / 150 = 8,2 mm
Obliczenie ugięć wykonano za pomocą programu RM-WIN.
Przemieszczenia równoległe |
Przemieszczenia prostopadłe |
od siły skupionej |
od siły skupionej |
|
|
uinst,z = 1,6 mm |
uinst,y = 4,2 mm |
od ciężaru własnego |
od ciężaru własnego |
|
|
uinst,z = 0,2 mm |
uinst,y = 0,2 mm |
Współczynnik kdef podano w zależności od klasy trwania obciążenia dla 2 klasy uzytkownia. Ugięcie finalne obliczono ze wzoru:
ufin, y = uinst, y ( 1+ kdef )
Zestawienie obliczonych ugięć
Obciążenie |
kdef |
Składowe równoległe [mm] |
Składowe prostopdałe [mm] |
||
|
|
uinst,z |
ufin, z |
uinst, y |
ufin, y |
Siła skupiona (obciąż. krótkotrwałe) |
0,0 |
1,6 |
1,6 |
4,2 |
4,2 |
Ciężar własny (obciąż. stałe) |
0,8 |
0,2 |
0,36 |
0,2 |
0,36 |
Ugięcie sumaryczne ufin, y = ufin, y1 + ufin, y2 |
1,96 |
4,56 |
|||
Ugięcie całkowite ufin, = (u2fin, y + u2fin, z )0,5 |
4,96 |
||||
ufin = 4,96mm < unet, fin = 8,2mm
Warunek stanu granicznego użytkowalności dla łaty został spełniony.
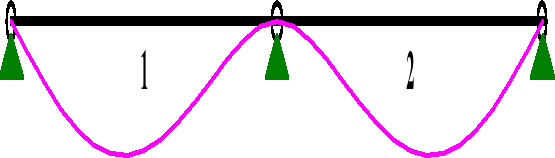
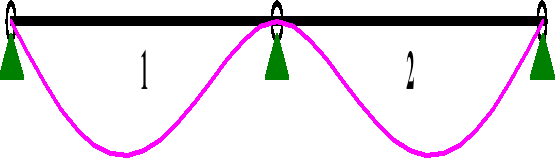
WARIANT II
Wykresy momentów zginających wykonano za pomocą programu RM-WIN.
a) WARTOŚCI SKŁADOWE PROSTOPADŁE OBCIĄŻENIA:
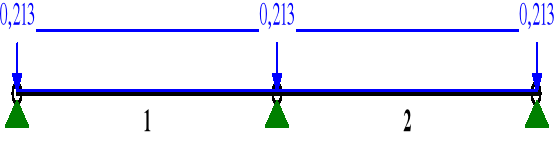
MOMENTY My:
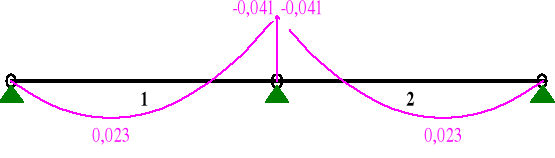
b) WARTOŚCI SKŁADOWE RÓWNOLEGŁE OBCIĄŻENIA:
MOMENTY Mz:
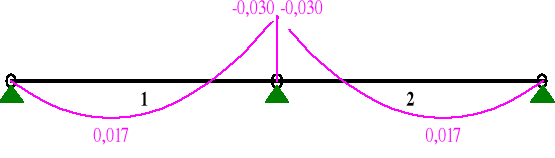
Wniosek:
Maksymalne momenty zginające w wariancie II są znacznie mniejsze niż w wariancie I. Ponadto wartość kmod=0,6 dla 2 klasy użytkowania przy obciążeniu stałym ( wariant II ) jest mniejsza od kmod=1,1 dla 2 klasy użytkowania przy obciążeniu zmiennym ( wariant I ). Nie ma więc potrzeby sprawdzania stanów granicznych łaty w wariancie II.
Ostatecznie przyjęto łatę o wymiarach przekroju poprzecznego 45 x 63 mm.
Poz. obl. 1.2. OBLICZENIE KROKWI
Przyjęto, że wiązar dachowy będzie wykonany z bali o grubości 80 mm. Krokwie 80 x 180 mm, kleszcze 50 x 150 mm. Przyjęto ocieplenie połaci dachowej wełna mineralną grubości 160 mm oraz szczelinę powietrzną nad wełną grubości 20 mm, odprowadzającą wilgoć.
Obciążenia
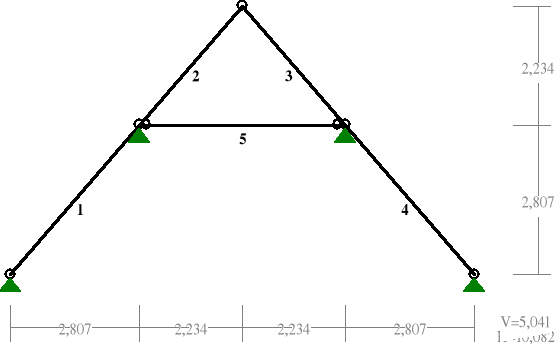
Schemat statyczny wiązara płatwiowo-kleszczowego:
Zestawienie obciążeń połaci dachowych
Obciążenie |
Wartość charaktery [kN/m] |
Wsp. obciążenia γf [-] |
Wartość obliczenio [kN/m] |
Wartości składowe prostopadłe obciążenia |
Wartości składowe równoległe obciążenia |
||
|
|
|
|
Charakter. [kN/m] |
Obliczeniowa [kN/m] |
Charakter [kN/m] |
Obliczeniowa [kN/m] |
Ciężar własny dachu z uwzględnieniem ciężaru krokwi i łączenia ciężar własny dachówki 9,81 ·10-3 · 2,3 · 16 · 1,24 ciężar własny łaty 0,016 · 100/28 · 1,24 ciężar własny krokwi 0,08 · 0,18 · 5,5
RAZEM: Śnieg połać lewa Sk =Qk · C2 =0,7·0,6 · 1,24 Połć prawa Sk =Qk · C1 =0,7·0,4 · 1,24 Wiatr połać nawietrzna pk1 = qk · Ce · C · β = =0,25·0,8·0,475·1,8·1,24 połać zawietrzna pk2 = qk · Ce · C · β = =0,25·0,8·(-0,400)·1,8·1,24 Ciężar własny kleszczy 2 · 0,05 · 0,15 · 5,5 Ocieplenie ciężar ocieplenia (200 mm wełny mineralnej 0,20 · 1,00 · 0,90 ciężar płyty g-k na ruszcie 0,0125 · 12,0 · 0,90
RAZEM |
gk = 0,448
gk1 = 0,071
gk2 = 0,079
gk = 0,598
Sk = 0,521
Sk = 0,347
pk1=+0,212
pk2=-0,179
gk3 = 0,083
0,180
0,125
0,305 |
1,2
1,1
1,1
1,5
1,5
1,3
1,3
1,1
1,2
1,2
|
gd = 0,538
gd1 = 0,078
gd2 = 0,087
gk = 0,672
Sd = 0,781
Sd = 0,521
pd1=+0,276
pd2=-0,166
gd3 = 0,091
0,216
0,162
0,378 |
0,317
0,050
0,056
0,423
0,261
0,173
+0,191*
-0,161*
0,127
0,088
0,215 |
0,380
0,055
0,062
0,497
0,391
0,261
+0,248*
-0,209*
0,152
0,114
0,266 |
0,317
0,050
0,056
0,423
0,261
0,173
0,127
0,088
0,215 |
0,380
0,055
0,062
0,497
0,391
0,261
0,152
0,114
0,266 |
Obciążenie skupione (człowiek obciążający kleszcze) [kN] |
Pk = 1,00 |
1,2 |
Pd = 1,20 |
|
|
|
|
* Uwzględniono współczynnik jednoczesności obciążeń Ψo = 0,9. |
|
||||||
Węzły wiązara płatwiowo-kleszczowego
Nr |
X [m] |
Y [m] |
Nr |
X [m] |
Y [m] |
1 2 3 |
0,000 2,807 5,041 |
0,000 2,807 5,041 |
4 5 |
7,275 10,082 |
2,807 0,000 |
Pręty wiązara płatwiowo-kleszczowego
Typy prętów: 00 - sztyw.-sztyw.; 01 - sztyw.-przegub;
10 - przegub-sztyw.; 11 - przegub-przegub
Pręt |
Typ |
A B |
Lx[m] |
Ly[m] |
L[m] |
Red.EJ |
Przekrój |
1 2 3 4 5
|
10 01 10 01 11 |
1 2 2 3 3 4 4 5 2 4
|
2,807 2,234 2,234 2,807 4,468 |
2,807 2,234 -2,234 -2,807 0,000 |
3,970 3,159 3,159 3,970 4,468 |
1,000 1,000 1,000 1,000 1,000 |
1 Krokiew 180 x 80 1 Krokiew 180 x 80 1 Krokiew 180 x 80 1 Krokiew 180 x 80 2 Kleszcze 150 x 50 |
Wielkości przekrojowe wiązara płatwiowo-kleszczowego
Nr |
A[cm2] |
Ix[cm4] |
Iy[cm4] |
Wg[cm3] |
Wd[cm3] |
h[cm] |
Materiał |
1 2 |
150,0 144,0 |
6650 3888 |
2812 768 |
375 432 |
375 432 |
15,0 18,0 |
Drewno C30 Drewno C30 |
Schemat obciążeń wiązara płatwiowo-kleszczowego
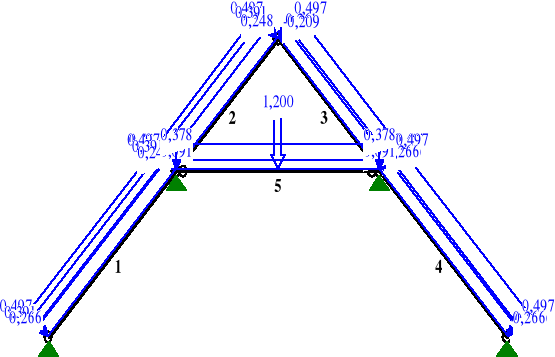
Wartości obciążeń poszczególnych pretów wiązara płatwiowo-kleszczowego ([kN],[kNm],[kN/m])
Pręt Rodzaj Kąt P1(Tg) P2(Td) a[m] b[m] |
Pręt: Rodzaj: Kąt: P1(Tg): P2(Td): a[m]: b[m]: ------------------------------------------------------------------ Grupa: A " Cięż. wł. pokrycia z krokwią " 1 Liniowe 45,0 0,497 0,497 0,00 3,97 1 Liniowe -45,0 0,497 0,497 0,00 3,97 2 Liniowe 45,0 0,497 0,497 0,00 3,16 2 Liniowe -45,0 0,497 0,497 0,00 3,16 3 Liniowe -45,0 0,497 0,497 0,00 3,16 3 Liniowe 45,0 0,497 0,497 0,00 3,16 4 Liniowe -45,0 0,497 0,497 0,00 3,97 4 Liniowe 45,0 0,497 0,497 0,00 3,97
Grupa: B " Śnieg " 1 Liniowe 45,0 0,391 0,391 0,00 3,97 1 Liniowe -45,0 0,391 0,391 0,00 3,97 2 Liniowe 45,0 0,391 0,391 0,00 3,16 2 Liniowe -45,0 0,391 0,391 0,00 3,16 3 Liniowe -45,0 0,261 0,261 0,00 3,16 3 Liniowe 45,0 0,261 0,261 0,00 3,16 4 Liniowe -45,0 0,261 0,261 0,00 3,97 4 Liniowe 45,0 0,261 0,261 0,00 3,97
Grupa: C " Wiatr " 1 Liniowe 45,0 0,248 0,248 0,00 3,97 2 Liniowe 45,0 0,248 0,248 0,00 3,16 3 Liniowe -45,0 -0,209 -0,209 0,00 3,16 4 Liniowe -45,0 -0,209 -0,209 0,00 3,97
Grupa: D " Ciężar własny kleszczy " 5 Liniowe 0,0 0,091 0,091 0,00 4,47
Grupa: E "Ocieplenie" 1 Liniowe 45,0 0,266 0,266 0,00 3,97 1 Liniowe -45,0 0,266 0,266 0,00 3,97 4 Liniowe -45,0 0,266 0,266 0,00 3,97 4 Liniowe 45,0 0,266 0,266 0,00 3,97 5 Liniowe 0,0 0,378 0,378 0,00 4,47
Grupa: F " Siła skupiona " 5 Skupione 0,0 1,200 2,23 |
Wartości sił przekrojowych w poszczególnych prętach wiązara płatwiowo-kleszczowego
Obciążenia obl.: ABCDE, T.I rzędu
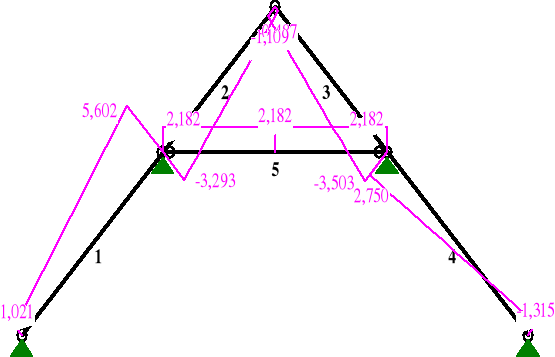
Pręt x/L x[m] M[kNm] Q[kN] N[kN] |
1 0,00 0,000 0,000 2,237 1,021 0,40 1,597 1,784* -0,002 2,864 1,00 3,970 -2,167 -3,329 5,602
2 0,00 0,000 -2,167 2,480 -3,293 0,69 2,184 0,541* -0,001 -1,353 1,00 3,159 0,000 -1,109 -0,487
3 0,00 0,000 0,000 0,487 -1,109 0,28 0,889 0,216* -0,001 -1,782 1,00 3,159 -1,201 -1,247 -3,503
4 0,00 0,000 -1,201 1,920 2,750 0,59 2,357 1,061* -0,001 0,336 1,00 3,970 -0,000 -1,315 -1,315
5 0,00 0,000 0,000 1,648 2,182 0,50 2,234 2,511* 0,600 2,182 1,00 4,468 0,000 -1,648 2,182 |
* = Wartości ekstremalne |
Wykresy sił przekrojowych wiązara płatwiowo-kleszczowego wykonano za pomocą programu RM-WIN.
MOMENTY:
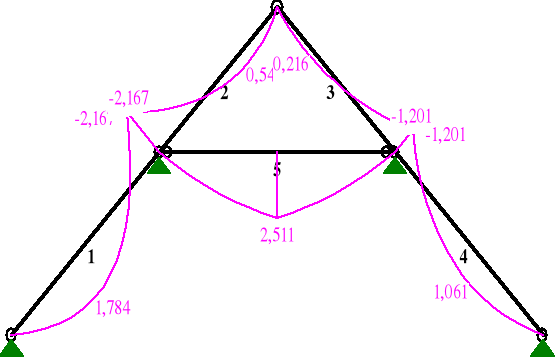
TNĄCE:
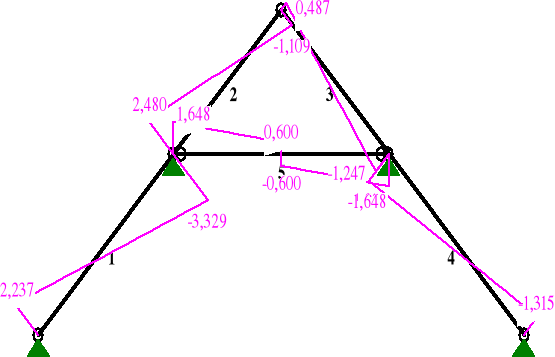
NORMALNE:
Wartości reakcji podporowych wiązara płatwiowo-kleszczowego.
Obciążenia obl.: ABCDE T.I rzędu
Węzeł H[kN] V[kN] Wypadkowa[kN] M[kNm] |
1 -2,304 0,860 2,459 2 -0,000 12,045 12,045 4 -0,000 8,309 8,309 5 -0,000 1,860 1,860 |
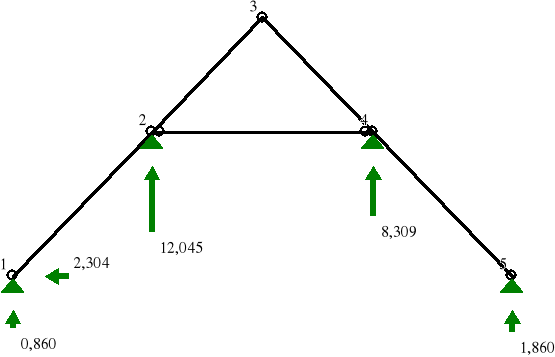
Wymiarowanie krokwi
Sprawdzenie stanu granicznego nośności
Maksymalny moment zginający i odpowiadająca mu siła osiowa wynoszą:
M1 = 1,784 kNm
N1 = + 2,864 kN (rozciąganie)
Przyjęto przekrój krokwi 80 x 180 mm. W miejscu oparcia krokwi na płatwi wykonano wcięcie o głębokości 40 mm. Przekrój netto wynosi więc 80 x 140 mm, stąd:
A = b · h = 0,080 · 0,140 = 11,2 · 10-3 m2
Wy = ( b · h2 ) / 6 = ( 0,080 · 0,1402 ) / 6 = 261,3 · 10-6 m3
Naprężenie obliczeniowe rozciągające w kierunku równoległym do włókien wynosi:
σt.0.d = N1 / A = 2,864 / ( 11,2 · 10-3 ) = 255,71 kPa = 0,255 MPa
Naprężenie obliczeniowe od zginania w stosunku do osi głównych wynosi:
σm.y.d = M1 / Wy = 1,784 / (261,3 · 10-6 ) = 6827,4 kPa = 6,83 MPa
σm.z.d = 0
Dla klasy drewna C30 wytrzymałość charakterystyczna na rozciąganie wynosi ft,0,k = 18 MPa, a na zginanie fm,y,k = 30 MPa. Wytrzymałość obliczeniową dla drewna na rozciąganie i zginanie przyjmując współczynnik γM = 1,3 i klasę użytkowania 2. Decydujące znaczenie ma obciążenie śniegiem ( średniotrwałe ), dlatego wartość współczynnika kmod = 0,8.
ft,0,d = ( kmod · ft,0,k ) / γM = ( 0,8 · 18 ) / 1,3 = 11,08 MPa
fm,y,d = ( kmod · fm,y,k ) / γM = ( 0,8 · 30 ) / 1,3 = 18,46 MPa
Sprawdzenie warunku stanu granicznego nośności:
(σt.0.d / ft,0,d) + (σm.y.d / fm,y,d) + km · (σm.z.d / fm,z,d) = (0,255 / 11,08) + (6,83 / 18,46) + 0 = 0,39 < 1
Warunek stanu granicznego nośności dla krokwi został spełniony.
Sprawdzenie stanu granicznego użytkowalności.
Wartość graniczną ugięcia krokwi obliczono ze wzoru:
unet, fin = L/200 = 3160 / 200 = 15,8 mm
Wykres ugięć krokwi.
ciężarem własnym
śniegiem
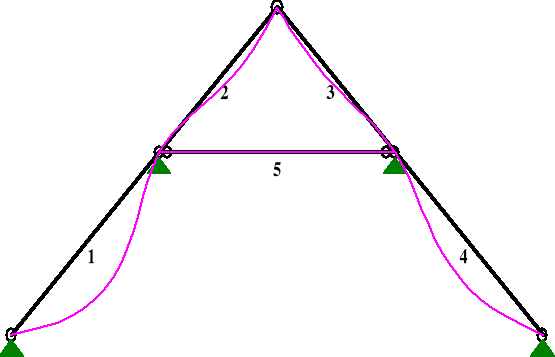
c) wiatrem
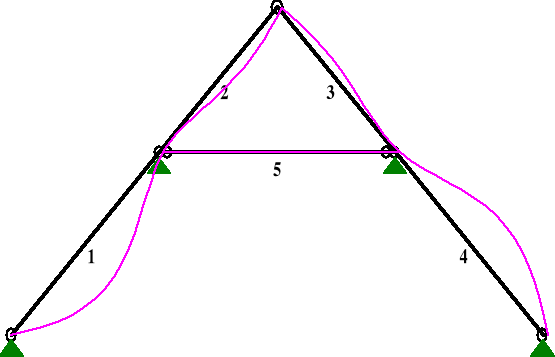
Wartości ugięcia krokwi od składowych obciążeń
Obciążenie |
kdef |
Składowe obciążenia [mm] |
|
|
|
uinst |
ufin, = uinst, ( 1+ kdef ) |
1. ciężar własny (klasa trwania obciążenia = = stałe, klasa użytkowania = 2) |
0,8 |
0,3 |
0,54 |
2. śnieg (klasa trwania obciążenia = = średniotrawałe, klasa użytkowania = 2) |
0,25 |
1,4 |
1,75 |
3. wiatr (klasa trwania obciążenia = = krótkotrwałe, klasa użytkowania =2) |
0 |
0,9 |
0,90 |
Ugięcie sumaryczne: ufin, = ufin, 1 + ufin,,2 + ufin,,3 |
3,19 |
||
ufin = 3,19 mm < 15,8 mm = unet, fin
Warunek stanu granicznego użytkowalności dla krokwi został spełniony.
Ostatecznie przyjęto krokiew o przekroju poprzecznym 80 x 180 mm.
Poz. obl. 1.3. OBLICZENIE KLESZCZY
Sprawdzenie stanu granicznego nośności
Maksymalny moment zginający wynosi:
M5 = 2,511 kNm
Maksymalna siła podłużna w kleszczach, określona dla wiązara pełnego i trzech wiązarów pustych wynosi:
N5 = 2,182· 4 = 8,728 kN (rozciąganie)
Przyjęto przekrój kleszczy 2 x 50 x 150, dla których:
A = 2b · h = 2 · 0,050 · 0,225 = 15 · 10-3 m2
Wy = 2 · (b · h2) / 6 = 2 · (0,050 · 0,1502) / 6 = 375,0 · 10-6 m3
Naprężenie obliczeniowe rozciągające w kierunku równoległym do włókien wynosi:
σt.0.d = N5 / A = 8,728 / (15 · 10-3) = 591,9 kPa = 0,592 MPa
Naprężenie obliczeniowe od zginania w stosunku do osi głównych wynosi:
σm.y.d = M5 / Wy = 2,511 / (375,0 · 10-6 ) = 6696,0 kPa = 6,70 MPa
σm.z.d = 0
W tym przypadku decydujące znaczenie ma obciążenie ciężarem człowieka (chwilowe). Dlatego wartość współczynnika kmod = 1,1. Zatem dla drewno C30 wytrzymałość obliczeniowa na rozciągnie i zginanie wynosi:
ft,0,d = ( kmod · ft,0,k ) / γM = ( 1,1 · 18 ) / 1,3 = 15,23 MPa
fm,y,d = ( kmod · fm,y,k ) / γM = ( 1,1 · 30 ) / 1,3 = 25,38 MPa
Sprawdzenie warunku stanu granicznego nośności:
(σt.0.d / ft,0,d) + (σm.y.d / fm,y,d) + km · (σm.z.d / fm,z,d) = (0,592 / 15,23) + (6,70 / 25,38) + 0 = 0,30 < 1
Warunek stanu granicznego nośności dla kleszczy został spełniony.
Sprawdzenie stanu granicznego użytkowalności
Wartość graniczną ugięcia kleszczy obliczono ze wzoru:
unet, fin = L/200 = 4468 / 200 = 22,34 mm
Wykres ugięć kleszczy.
ciężarem własnym
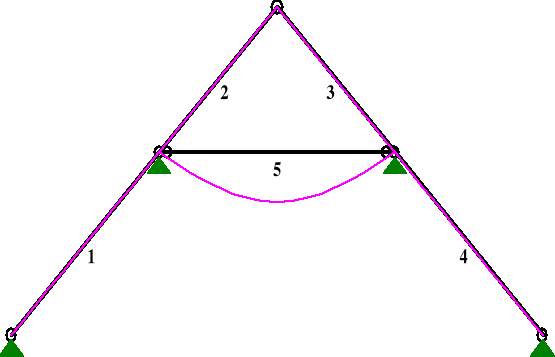
siłą skupioną
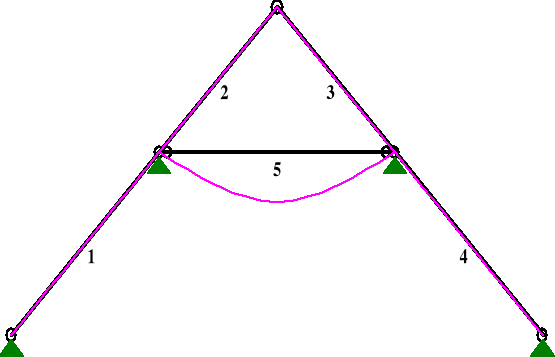
Wartości ugięcia kleszczy od składowych obciążeń
Obciążenie |
kdef |
Składowe obciążenia [mm] |
|
|
|
uinst |
ufin, = uinst, ( 1+ kdef ) |
1. ciężar własny (klasa trwania obciążenia = = stałe, klasa użytkowania = 2) |
0,8 |
7,2 |
12,96 |
2. siła skupiona (klasa trwania obciążenia = = krótkotrwałe, klasa użytkowania =2) |
0 |
6,6 |
6,60 |
Ugięcie sumaryczne ufin, = ufin, 1 + ufin,,2 |
19,56 |
||
ufin = 19,56 < 22,34mm = unet, fin
Warunek stanu granicznego użytkowalności dla kleszczy został spełniony.
Ostatecznie przyjęto kleszcze o przekroju poprzecznym 50 x 150 mm.
Poz. obl. 1.4. OBLICZENIE PŁATWI
Przyjęto do obliczeń płatew o przekroju poprzecznym 150 x 175 mm. Jako schemat statyczny przyjęto ramę
dwuprzesłową.
Schemat statyczny przyjęty do obliczenia płatwi z opisem prętów:
płaszczyzna pionowa:
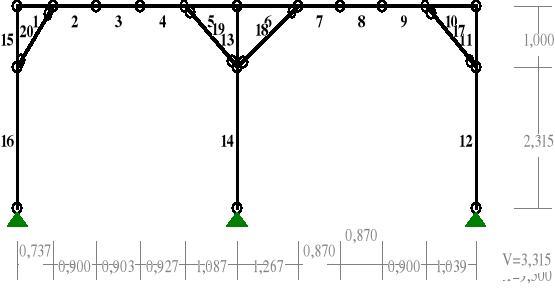
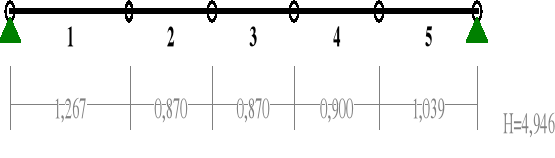
płaszczyzna pozioma:
Zestawienie obciążeń na płatew
Na płatew działa obciążenie z odcinka górnego i połowy odcinka dolnego krokwi, tj. pasma szerokości:
3,160 + 0,5 · 3,970 = 5,145 m.
Obciążenie |
Wartość charaktery [kN/m] |
Wsp. obciążen γf [-] |
Wartość obliczenio [kN/m] |
Wartości składowe prostopadłe obciążenia |
Wartości składowe równoległe obciążenia |
||
|
|
|
|
Charakter. [kN/m] |
Obliczeniowa [kN/m] |
Charakter [kN/m] |
Obliczeniowa [kN/m] |
Ciężar własny dachu z uwzględnieniem ciężaru krokwi i łacenia ciężar własny dachówki 9,81·10-3 · 2,3 · 16 · 1,24·5,145 ciężar własny łaty 0,016 · 100/28 · 1,24 ·5,145 ciężar własny krokwi 0,08 · 0,18 · 5,5· 5,145 ciężar własny kleszczy 2 · 0,05 · 0,15 · 5,5 Ocieplenie ciężar ocieplenia (200 mm wełny mineralnej 0,20·1,00·0,90·0,5·(3,970+ 4,468) ciężar płyty g-k na ruszcie 0,0125·12,0·0,90·0,5·(3,970+ 4,468) ciężar własny płatwi 0,150 · 0,175 · 5,5 Śnieg połać lewa Sk =Qk ·C2 =0,7·0,6·1,24·5,145 Wiatr połać nawietrzna pk1 = qk · Ce · C · β = =0,25·0,8·0,475·1,8·1,24·5,145
|
gk = 2,303
gk1 = 0,365
gk2 = 0,407
gk3 = 0,083
gk5 = 0,759
gk6 = 0,557
gk4 = 0,144
Sk = 2,680
pk1=1,091 |
1,2
1,1
1,1
1,1
1,2
1,2
1,1
1,5
1,3
|
gd = 2,764
gd1 = 0,402
gd2 = 0,448
gd3 = 0,091
gk5 = 0,911
gk6 = 0,669
gd4 = 0,158
Sd = 4,019
pd1=1,418
|
2,303
0,365
0,407
0,083
0,759
0,557
0,102
1,895
0,694* |
2,764
0,402
0,448
0,091
0,911
0,669
0,112
2,842
0,902* |
0,694* |
0,902* |
* Uwzględniono współczynnik jednoczesności obciążeń Ψo = 0,9. |
|||||||
W związku z tym:
składowa pionowa obciążenia wynosi:
qkz = qkz +qkz1+qkz2+qkz3+qkz4+Skz+pkz+qdz5 +qdz6 = 7,165 kN/m
qdz = qdz +qdz1+qdz2+qdz3+qdz4+Sdz+pdz+qdz5 +qdz6 = 9,141 kN/m
składowa pozioma obciążenia wynosi:
qky = pky = 0,694 kN/m
qdy = pdy = 0,902 kN/m
Wyznaczanie sił wewnętrznych
Węzły ramy dwuprzęsłowej
Nr |
X [m] |
Y [m] |
Nr |
X [m] |
Y [m] |
1 2 3 4 5 6 7 8 9
|
0,000 0,737 1,637 2,540 3,467 4,554 5,821 6,691 7,561
|
3,315 3,315 3,315 3,315 3,315 3,315 3,315 3,315 3,315 |
10 11 12 13 14 15 16 17
|
8,461 9,500 9,500 4,554 4,554 0,000 0,000 9,500
|
3,315 3,315 0,000 0,000 2,315 0,000 2,315 2,315
|
Pręty ramy dwuprzęsłowej
Typy prętów: 00 - sztyw.-sztyw.; 01 - sztyw.-przegub;
10 - przegub-sztyw.; 11 - przegub-przegub
Pręt Typ A B Lx[m] Ly[m] L[m] Red.EJ Przekrój |
1 10 1 2 0,737 0,000 0,737 1,000 3 płatew 175x150 2 00 2 3 0,900 0,000 0,900 1,000 3 płatew 175x150 3 00 3 4 0,903 0,000 0,903 1,000 3 płatew 175x150 4 00 4 5 0,927 0,000 0,927 1,000 3 płatew 175x150 5 01 5 6 1,087 0,000 1,087 1,000 3 płatew 175x150 6 10 6 7 1,267 0,000 1,267 1,000 3 płatew 175x150 7 00 7 8 0,870 0,000 0,870 1,000 3 płatew 175x150 8 00 8 9 0,870 0,000 0,870 1,000 3 płatew 175x150 9 00 9 10 0,900 0,000 0,900 1,000 3 płatew 175x150 10 01 10 11 1,039 0,000 1,039 1,000 3 płatew 175x150 11 10 11 17 0,000 -1,000 1,000 1,000 2 słup 150x150 12 01 17 12 0,000 -2,315 2,315 1,000 2 słup 150x150 13 10 6 14 0,000 -1,000 1,000 1,000 2 słup 150x150 14 01 14 13 0,000 -2,315 2,315 1,000 2 słup 150x150 15 10 1 16 0,000 -1,000 1,000 1,000 2 słup 150x150 16 01 16 15 0,000 -2,315 2,315 1,000 2 słup 150x150 17 11 17 10 -1,039 1,000 1,442 1,000 1 miecz 150x100 18 11 7 14 -1,267 -1,000 1,614 1,000 1 miecz 150x100 19 11 14 5 -1,087 1,000 1,477 1,000 1 miecz 150x100 20 11 2 16 -0,737 -1,000 1,242 1,000 1 miecz 150x100
|
Wielkości przekrojowe ramy dwuprzęsłowej
Nr. A[cm2] Ix[cm4] Iy[cm4] Wg[cm3] Wd[cm3] h[cm] Materiał |
1 150,0 2812 1250 375 375 15,0 25 DrewnoC30 2 225,0 4219 4219 563 563 15,0 25 DrewnoC30 3 262,5 6699 4922 766 766 17,5 25 DrewnoC30 |
Schemat obciążeń ramy w płaszczyźnie pionowej
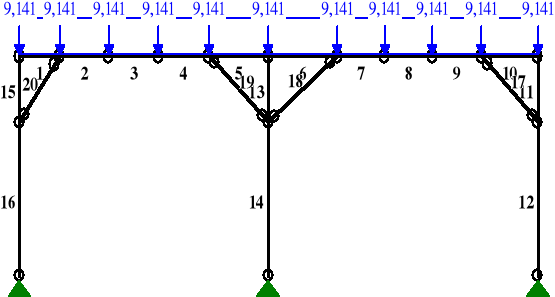
Wartości obciążeń na poszczególnych prętach ramy ([kN],[kNm],[kN/m])
Pręt Rodzaj Kąt P1(Tg) P2(Td) a[m] b[m] |
Grupa: A "Suma obciążeń" 1 Liniowe 0,0 9,141 9,141 0,00 0,74 2 Liniowe 0,0 9,141 9,141 0,00 0,90 3 Liniowe 0,0 9,141 9,141 0,00 0,90 4 Liniowe 0,0 9,141 9,141 0,00 0,93 5 Liniowe 0,0 9,141 9,141 0,00 1,09 6 Liniowe 0,0 9,141 9,141 0,00 1,27 7 Liniowe 0,0 9,141 9,141 0,00 0,87 8 Liniowe 0,0 9,141 9,141 0,00 0,87 9 Liniowe 0,0 9,141 9,141 0,00 0,90 10 Liniowe 0,0 9,141 9,141 0,00 1,04 |
Wartości sił przekrojowych w poszczególnych prętach ramy w płaszczyźnie pionowej
Obciążenia obl.: ABCD, T.I rzędu
Pręt x/L x[m] M[kNm] Q[kN] N[kN] |
1 0,00 0,000 0,000 6,667 4,211 0,99 0,728 2,431 0,009 4,211 1,00 0,737 2,431 -0,070 4,211
2 0,00 0,000 2,431 8,112 -1,819 0,99 0,889 6,030 -0,019 -1,819 0,98 0,886 6,030 0,013 -1,819 1,00 0,900 6,030 -0,115 -1,819
3 0,00 0,000 6,030 -0,115 -1,819 1,00 0,903 2,199 -8,369 -1,819
4 0,00 0,000 2,199 -8,369 -1,819 1,00 0,927 -9,487 -16,843 -1,819
5 0,00 0,000 -9,487* 13,696 31,377 1,00 1,087 0,000 3,760 31,377
6 0,00 0,000 0,000 0,013 33,045 1,00 1,267 -7,321 -11,569 33,045
7 0,00 0,000 -7,321 16,517 -2,539 1,00 0,870 3,589 8,564 -2,539
8 0,00 0,000 3,589 8,564 -2,539 1,00 0,870 7,580 0,611 -2,539
9 0,00 0,000 7,580 0,611 -2,539 0,07 0,067 7,601 0,001 -2,539 1,00 0,900 4,428 -7,616 -2,539
10 0,00 0,000 4,428 0,487 5,879 0,05 0,053 4,441 0,004 5,879 1,00 1,039 0,000 -9,011 5,879
11 0,00 0,000 0,000 -5,879 -9,011 1,00 1,000 -5,879 -5,879 -9,011
12 0,00 0,000 -5,879 2,539 -17,113 1,00 2,315 0,000 2,539 -17,113
13 0,00 0,000 0,000 1,668 3,747 1,00 1,000 1,668 1,668 3,747
14 0,00 0,000 1,668 -0,720 -54,878 1,00 2,315 -0,000 -0,720 -54,878
15 0,00 0,000 0,000 4,211 -6,667 1,00 1,000 4,211 4,211 -6,667
16 0,00 0,000 4,211 -1,819 -14,849 1,00 2,315 -0,000 -1,819 -14,849
17 0,00 0,000 0,000 0,000 -11,684 1,00 1,442 0,000 0,000 -11,684
18 0,00 0,000 0,000 0,000 -45,332 1,00 1,614 0,000 0,000 -45,332
19 0,00 0,000 0,000 0,000 -45,107 1,00 1,477 0,000 0,000 -45,107
20 0,00 0,000 0,000 0,000 -10,164 1,00 1,242 0,000 0,000 -10,164
|
* = Wartości ekstremalne |
Wykresy sił przekrojowych dla ramy w płaszczyźnie pionowej wykonano za pomocą programu RM-WIN.
MOMENTY:
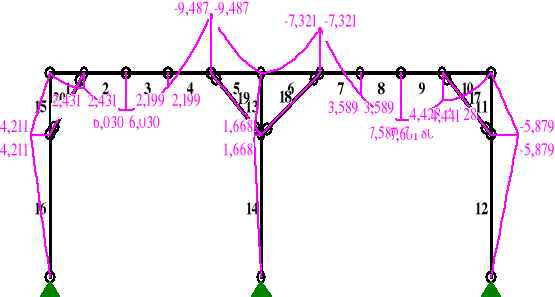
TNĄCE:
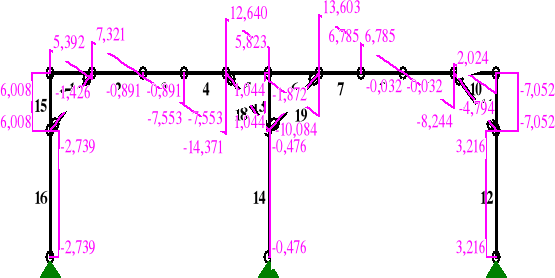
NORMALNE:
NORMALNE:
Schemat obciążeń ramy w płaszczyźnie poziomej
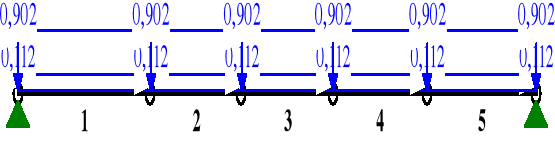
Wartości obciążeń na poszczególnych prętach ramy ([kN],[kNm],[kN/m])
Pręt Rodzaj Kąt P1(Tg) P2(Td) a[m] b[m] |
Grupa: A "Ciężar własny płatwi" 1 Liniowe 0,0 0,112 0,112 0,00 1,27 2 Liniowe 0,0 0,112 0,112 0,00 0,87 3 Liniowe 0,0 0,112 0,112 0,00 0,87 4 Liniowe 0,0 0,112 0,112 0,00 0,90 5 Liniowe 0,0 0,112 0,112 0,00 1,04
Grupa: B "Obciążenie wiatrem" 1 Liniowe 0,0 0,902 0,902 0,00 1,27 2 Liniowe 0,0 0,902 0,902 0,00 0,87 3 Liniowe 0,0 0,902 0,902 0,00 0,87 4 Liniowe 0,0 0,902 0,902 0,00 0,90 5 Liniowe 0,0 0,902 0,902 0,00 1,04
|
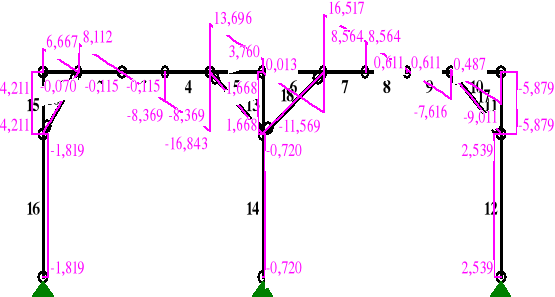
Wykresy sił przekrojowych dla ramy w płaszczyźnie pionowej wykonano za pomocą programu RM-WIN.
MOMENTY:
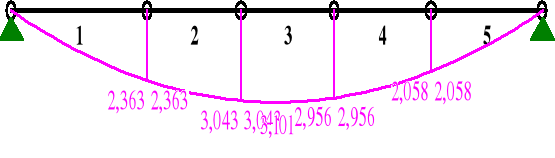
TNĄCE:
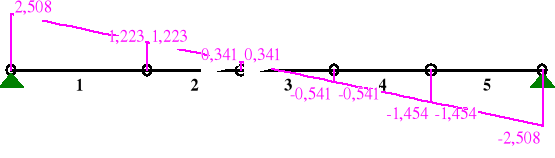
NORMALNE:
Wartości sił przekrojowych w poszczególnych prętach ramy w płaszczyźnie pionowej
Obciążenia obl.: AB, T.I rzędu
Pręt x/L x[m] M[kNm] Q[kN] N[kN] |
1 0,00 0,000 0,000 2,508 0,000 1,00 1,267 2,363 1,223 0,000
2 0,00 0,000 2,363 1,223 0,000 1,00 0,870 3,043 0,341 0,000
3 0,00 0,000 3,043 0,341 0,000 0,39 0,340 3,101 -0,004 0,000 0,38 0,333 3,101 0,003 0,000 1,00 0,870 2,956 -0,541 0,000
4 0,00 0,000 2,956 -0,541 0,000 1,00 0,900 2,058 -1,454 0,000
5 0,00 0,000 2,058* -1,454 0,000 1,00 1,039 -0,000 -2,508 0,000 |
* = Wartości ekstremalne |
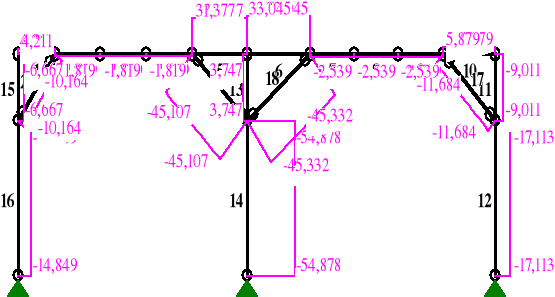
Sprawdzenie stanu granicznego nośności
Maksymalny moment zginający i odpowiadająca mu siła podłużna występuje w pręcie 5 i wynoszą:
My = 9,487 kNm
N = 31,377 kN (rozciąganie)
Mz = 2,058 kNm
Przyjęto przekrój płatwi 150 x 175 mm, dla którego:
A = b · h = 0,150 · 0,175 = 26,25 · 10-3 m2
Wy = ( b · h2 ) / 6 = ( 0,150 · 0,1752 ) / 6 = 765,625 · 10-6 m3
Wz = ( b2 · h ) / 6 = ( 0,1502 · 0,175 ) / 6 = 393,750 · 10-6 m3
Naprężenie obliczeniowe rozciągające w kierunku równoległym do włókien wynosi:
σt.0.d = N / A = 31,377 / (26,25 · 10-3) = 1195,3 kPa = 1,139 MPa
Naprężenie obliczeniowe od zginania w stosunku do osi głównych wynosi:
σm.y.d = My / Wy = 9,487 / (765,625 · 10-6 ) = 12391,2 kPa = 12,178 MPa
σm.z.d = Mz / Wz = 2,058 / (393,750 · 10-6 ) = 5226,7 kPa = 5,203 MPa
Decydujące znaczenie ma obciążenie śniegiem ( średniotrwałe ), dlatego wartość współczynnika kmod = 0,8. Zatem wytrzymałość obliczeniową dla drewna klasy C30 na rozciąganie i zginanie wynosi:
ft,0,d = ( kmod · ft,0,k ) / γM = ( 0,8 · 18 ) / 1,3 = 11,08 MPa
fm,y,z,d = ( kmod · fm,y,k ) / γM = ( 0,8 · 30 ) / 1,3 = 18,46 MPa
Sprawdzenie warunku stanu granicznego nośności:
(σt.0.d / ft,0,d) + (σm.y.d / fm,y,d) + km · (σm.z.d / fm,z,d) =
= (1,139 / 11,08) + (12,178 / 18,46) + 0,8 · (5,203 / 18,46) = 0,988 < 1
Warunek stanu granicznego nośności dla płatwi został spełniony.
Sprawdzenie stanu granicznego użytkowalności
Graniczne ugiecie płatwi obliczono ze wzoru:
unet, fin = L/200 = 4946 / 200 = 24,73 mm
Wartości ugięcia płatwi od składowych obciążeń
Obciążenie |
kdef |
Składowe obciążenia [mm] |
||
|
|
uinst |
ufin, = uinst, ( 1+ kdef ) |
|
pionowe (z) |
1. ciężar własny (klasa trwania obciążenia = = stałe, klasa użytkowania = 2) |
0,8 |
0,5 |
0,90 |
|
2. śnieg (klasa trwania obciążenia = = średniotrwałe, klasa użytkowania = 2) |
0,25 |
0,3 |
0,38 |
|
3a. wiatr (klasa trwania obciążenia = = krótkotrwałe, klasa użytkowania =2) |
0 |
0,2 |
0,20 |
poziome (y) |
3b. wiatr (klasa trwania obciążenia = = krótkotrwałe, klasa użytkowania = 2) |
0 |
0,4 |
0,40 |
Ugięcie sumaryczne ufin, = ( u2fin,z + u2fin,y )0,5 = |
1,53 |
|||
ufin = 1,53 mm < 24,73 mm = unet, fin
Wykresy ugięć od obciążenia:
a) ciężarem własnym:

b)śniegiem
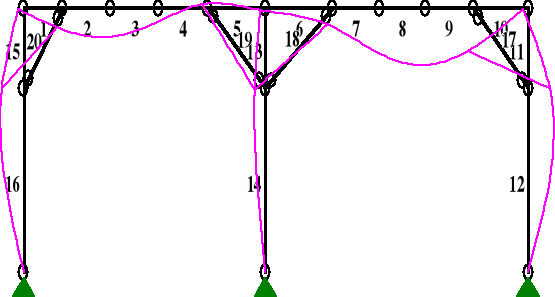
c)wiatrem pionowo
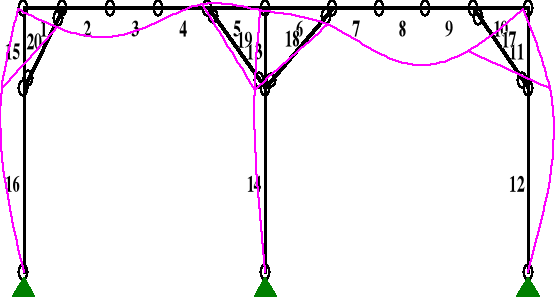
d)wiatrem poziomo
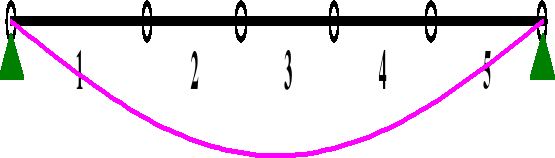
Warunek stanu granicznego nośności dla płatwi został spełniony.
Ostatecznie przyjęto płatwie o przekroju poprzecznym 150 x 175 mm.
Poz. obl. 1.5. OBLICZENIE SŁUPA
Słup obliczono jako ściskany osiowo siłą P = 54,878 kN. Do wymiarowania przyjęto przekrój słupa 150 x 150 mm, dla którego:
A = b · h = 150 · 150 = 22500 mm2 = 22,5 · 10-3 m2
Iy = Ix = a4 / 12 = 1504 / 12 = 4218,75 · 104 mm4
iy = ( I / A )0,5 = ( 4218,75 · 104 / 22500 ) = 43,30 mm
ly = 3315 mm
lz = 3315 - 1000 = 2315 mm < ly - zatem lz pominięto w dalszych obliczeniach.
Smukłość względna osi y wynosi:
λy = ly / iy = 3315 / 43,30 = 76,56
σc,crit,y = π2 · E0,05 / λ2y = π2 · 6700 / 76,562 = 11,28 MPa
λrel.y = ( fc,0,k / σc,crit,y )0,5 = ( 20,00 / 11,28)0,5 = 1,33
βc = 0,2 (drewno lite)
ky = 0,5 · [ 1 + βc · ( λrel.y - 0,5 ) + λ2 rel.y ] = 0,5 · [ 1 + 0,2 · ( 1,33 - 0,5 ) + 1,332 ] = 1,467
kc,y = 1 / [ ky + ( k2y - λ2rel,y )0,5 ] = 1 / [ 1,467 + ( 1,4672 - 1,332 )]0,5 = 0,735
Naprężenie obliczeniowe ściskające w kierunku równoległym do włókien wynosi:
σc,0,d = P / A = 54,878 / (22,5 · 10-3 ) = 2439,0 kPa = 2,44 MPa
Dla klasy drewna C30 wytrzymałość charakterystyczna na ściskanie wynosi: fc,0,k = 23,0 MPa. Decydujące znaczenie ma obciągnie śniegiem ( średniotrwałe ), dlatego wartość współczynnika kmod = 0,8, zatem:
fc,0,d = ( kmod · fc,0,k ) / γM = ( 0,8 · 23,0 ) / 1,3 = 14,15 MPa
Sprawdzenie warunku stanu granicznego nośności
σc,0,d = 2,44 < kc,y · fc,0,d = 0,735 · 14,15 = 10,40 MPa
Warunek stanu granicznego nośności dla słupa został spełniony.
Sprawdzanie docisku słupa do płatwi
Powierzchnia docisku słupa do płatwi ( brak czopu, usztywnienie połączenia płatwi ze słupem przez nakładki z blachy stalowej perforowanej ) wynosi:
Ad = 150 · 150 = 22500 mm2 = 22,5 · 10-3 mm2
Wytrzymałość obliczeniowa na docisk wynosi:
fc,90,d = ( kmod · fc,90,k ) / γM = ( 0,8 · 2,7 ) / 1,3 = 1,66 MPa
Sprawdzenie naprężeń dokonano dla siły P działającej w górnym odcinku słupa i wynoszącej P = 9,011 kN.
σc,90,d = P / Ad = 9,011 / (22,5 · 10-3 ) = 360,4 kPa = 0, 36 MPa
Wartość współczynnika kc,90 = 1, dla a = 0 ( koniec płatwi opiera się na słupie ).
σc,90,d = 0,36 MPa < kc,90 · fc,90,d = 1 · 1,66 MPa
Warunek docisku słupa do płatwi został spełniony.
Ostatecznie przyjęto słup o przekroju 150 x 150 mm.
Poz. obl. 1.6. OBLICZENIE MIECZY
Zaprojektowano połączenie płatwi z mieczami za pomocą blachy perforowanej, zatem szerokość mieczy musi być taka sama jak szerokość płatwi. W konstrukcji wyróżniono dwa typy mieczy, dla których przyjęto krawędziaki o polu przekroju 150 x 100 mm.
Długość:
l1 = ( 1,002 + 0,7272 )0,5 = 1,236 m
l2 = ( 1,002 + 1,0872 )0,5 = 1,477 m
l3 = ( 1,002 + 1,2672 )0,5 = 1,614 m
l4 = ( 1,002 + 1,0392 )0,5 = 1,442 m
Obliczenia dla l1
Miecz obliczono jako ściskany osiowo siła S = 10,164 kN dla którego:
A = b · h = 150 · 100 = 15000 mm2 = 15,0 · 10-3 mm2
Iy = ( b · h3 ) / 12 = ( 150 · 1003 ) / 12 = 1250,00 · 104 mm4
iy = ( Iy / A )0,5 = ( 1250,00 · 104 / 15000 )0,5 = 28,87 mm
ly = lz = 1236 mm
Smukłość wzgledem osi y wynosi:
λy = ly / iy = 1236 / 28,87 = 42,81
σc,crit,y = π2 · E0,05 / λ2y = π2 · 6700 / 42,812 = 36,08 MPa
λrel.y = ( fc,0,k / σc,crit,y )0,5 = ( 20,00 / 36,08 )0,5 = 0,74
βc = 0,2 (drewno lite)
ky = 0,5 · [ 1 + βc · ( λrel.y - 0,5 ) + λ2 rel.y ] = 0,5 · [ 1 + 0,2 · ( 0,74 - 0,5 ) + 0,742 ] = 0,798
kc,y = 1 / [ ky + ( k2y - λ2rel,y )0,5 ] = 1 / [ 0,798 + ( 0,7982 - 0,742 )]0,5 = 1,062
Naprężenie obliczeniowe ściskające w kierunku równoległym do włókien wynosi:
σc,0,d = S / Ad = 10,164 / (15,0 · 10-3 ) = 1026,4 kPa = 1,03 MPa
Dla klasy drewna C30 wytrzymałość charakterystyczna na ściskanie wynosi: fc,0,k = 23,0 MPa. Decydujące znaczenie ma obciągnie śniegiem ( średniotrwałe ), dlatego wartość współczynnika kmod = 0,8, zatem:
fc,0,d = ( kmod · fc,0,k ) / γM = ( 0,8 · 23,0 ) / 1,3 = 14,15 MPa
Sprawdzenie warunku stanu granicznego nośności
σc,0,d = 1,03 MPa < kc,y · fc,0,d = 1,062 · 14,15 = 15,07 MPa
Warunek stanu granicznego nośności dla miecza został spełniony.
Obliczenia dla l2
Miecz obliczono jako ściskany osiowo siła S = 45,107 kN dla którego:
A = b · h = 150 · 100 = 15000 mm2 = 15,0 · 10-3 mm2
Iy = ( b · h3 ) / 12 = ( 150 · 1003 ) / 12 = 1250,00 · 104 mm4
iy = ( Iy / A )0,5 = ( 1250,00 · 104 / 15000 )0,5 = 28,87 mm
ly = lz = 1477 mm
Smukłość wzgledem osi y wynosi:
λy = ly / iy = 1477 / 28,87 = 51,16
σc,crit,y = π2 · E0,05 / λ2y = π2 · 6700 / 51,162 = 25,26 MPa
λrel.y = ( fc,0,k / σc,crit,y )0,5 = ( 20,00 / 25,26)0,5 = 0,89
βc = 0,2 (drewno lite)
ky = 0,5 · [ 1 + βc · ( λrel.y - 0,5 ) + λ2 rel.y ] = 0,5 · [ 1 + 0,2 · ( 0,89- 0,5 ) + 0,892 ] = 0,935
kc,y = 1 / [ ky + ( k2y - λ2rel,y )0,5 ] = 1 / [0,935 + (0,9352 - 0,892 )]0,5 = 0,991
Naprężenie obliczeniowe ściskające w kierunku równoległym do włókien wynosi:
σc,0,d = S / Ad = 45,107 / (15,0 · 10-3 ) = 3007,1 kPa = 3,00 MPa
Dla klasy drewna C30 wytrzymałość charakterystyczna na ściskanie wynosi: fc,0,k = 23,0 MPa. Decydujące znaczenie ma obciągnie śniegiem ( średniotrwałe ), dlatego wartość współczynnika kmod = 0,8, zatem:
fc,0,d = ( kmod · fc,0,k ) / γM = ( 0,8 · 23,0 ) / 1,3 = 14,15 MPa
Sprawdzenie warunku stanu granicznego nośności
σc,0,d = 2,47 MPa < kc,y · fc,0,d = 0,991 · 14,15 = 14,02 MPa
Warunek stanu granicznego nośności dla miecza został spełniony.
Obliczenia dla l3
Miecz obliczono jako ściskany osiowo siła S = 45,332 kN dla którego:
A = b · h = 150 · 100 = 15000 mm2 = 15,0 · 10-3 mm2
Iy = ( b · h3 ) / 12 = ( 150 · 1003 ) / 12 = 1250,00 · 104 mm4
iy = ( Iy / A )0,5 = ( 1250,00 · 104 / 15000 )0,5 = 28,87 mm
ly = lz = 1614 mm
Smukłość wzgledem osi y wynosi:
λy = ly / iy = 1614 / 28,87 = 55,91
σc,crit,y = π2 · E0,05 / λ2y = π2 · 6700 / 55,912 = 21,15 MPa
λrel.y = ( fc,0,k / σc,crit,y )0,5 = ( 20,00 / 21,15)0,5 = 0,97
βc = 0,2 (drewno lite)
ky = 0,5 · [ 1 + βc · ( λrel.y - 0,5 ) + λ2 rel.y ] = 0,5 · [ 1 + 0,2 · ( 0, 97 - 0,5 ) + 0, 972 ] = 1,017
kc,y = 1 / [ ky + ( k2y - λ2rel,y )0,5 ] = 1 / [1,017 + (1,0172 - 0, 972 )]0,5 = 0,949
Naprężenie obliczeniowe ściskające w kierunku równoległym do włókien wynosi:
σc,0,d = S / Ad = 45,332 / (15,0 · 10-3 ) = 3022,1 kPa = 3,02 MPa
Dla klasy drewna C30 wytrzymałość charakterystyczna na ściskanie wynosi: fc,0,k = 23,0 MPa. Decydujące znaczenie ma obciągnie śniegiem ( średniotrwałe ), dlatego wartość współczynnika kmod = 0,8, zatem:
fc,0,d = ( kmod · fc,0,k ) / γM = ( 0,8 · 23,0 ) / 1,3 = 14,15 MPa
Sprawdzenie warunku stanu granicznego nośności
σc,0,d = 3,02 MPa < kc,y · fc,0,d = 0,949· 14,15 = 13,43 MPa
Warunek stanu granicznego nośności dla miecza został spełniony.
Obliczenia dla l4
Miecz obliczono jako ściskany osiowo siła S = 11,684 kN dla którego:
A = b · h = 150 · 100 = 15000 mm2 = 15,0 · 10-3 mm2
Iy = ( b · h3 ) / 12 = ( 150 · 1003 ) / 12 = 1250,00 · 104 mm4
iy = ( Iy / A )0,5 = ( 1250,00 · 104 / 15000 )0,5 = 28,87 mm
ly = lz = 1442 mm
Smukłość wzgledem osi y wynosi:
λy = ly / iy = 1442 / 28,87 = 49,94
σc,crit,y = π2 · E0,05 / λ2y = π2 · 6700 / 49,942 = 26,51 MPa
λrel.y = ( fc,0,k / σc,crit,y )0,5 = ( 20,00 / 26,51)0,5 = 0,87
βc = 0,2 (drewno lite)
ky = 0,5 · [ 1 + βc · ( λrel.y - 0,5 ) + λ2 rel.y ] = 0,5 · [ 1 + 0,2 · ( 0,87- 0,5 ) + 0,872 ] = 0,915
kc,y = 1 / [ ky + ( k2y - λ2rel,y )0,5 ] = 1 / [0,915 + (0,9152 - 0,872 )]0,5 = 1,002
Naprężenie obliczeniowe ściskające w kierunku równoległym do włókien wynosi:
σc,0,d = S / Ad = 11,684 / (15,0 · 10-3 ) = 778,9 kPa = 0,78 MPa
Dla klasy drewna C30 wytrzymałość charakterystyczna na ściskanie wynosi: fc,0,k = 23,0 MPa. Decydujące znaczenie ma obciągnie śniegiem ( średniotrwałe ), dlatego wartość współczynnika kmod = 0,8, zatem:
fc,0,d = ( kmod · fc,0,k ) / γM = ( 0,8 · 23,0 ) / 1,3 = 14,15 MPa
Sprawdzenie warunku stanu granicznego nośności
σc,0,d = 0,78 MPa < kc,y · fc,0,d = 1,002 · 14,15 = 14,17 MPa
Warunek stanu granicznego nośności dla miecza został spełniony.
Ostatecznie przyjęto miecze o przekroju 150 x 100 mm.
6
Wyszukiwarka