8 16.0000 2.756373558E-0001 6.70E-0013

9 18.0000 3.090169944E-0001 1.18E-0013

10 20.0000 3.420201433E-0001 1.09E-0013

11 22.0000 3.746065934E-0001 3.19E-0014

12 24.0000 4.067366431E-0001 1.63E-0012

13 26.0000 4.383711468E-0001 4.46E-0012

14 28.0000 4.694715628E-0001 1.00E-0011

15 30.0000 5.000000000E-0001 2.06E-0011

16 32.0000 5.299192642E-0001 9.23E-0013

17 34.0000 5.591929035E-0001 6.60E-0013

18 36.0000 5.877852523E-0001 7.22E-0013

19 38.0000 6.156614753E-0001 3.81E-0013

20 40.0000 6.427876097E-0001 1.43E-0012

21 42.0000 6.691306064E-0001 2.53E-0012

22 44.0000 6.946583705E-0001 4.34E-0012

23 46.0000 7.193398003E-0001 9.43E-0012

24 48.0000 7.431448255E-0001 1.58E-0011

25 50.0000 7.660444431E-0001 2.79E-0011

26 52.0000 7.880107536E-0001 4.56E-0011

27 54.0000 8.090169944E-0001 4.78E-0013

28 56.0000 8.290375726E-0001 2.89E-0013

29 58.0000 8.480480962E-0001 6.00E-0013

30 60.0000 8.660254038E-0001 2.01E-0012

31 62.0000 8.829475929E-0001 3.66E-0012

32 64.0000 8.987940463E-0001 3.77E-0012

33 66.0000 9.135454576E-0001 6.06E-0012

34 68.0000 9.271838546E-0001 9.83E-0012

35 70.0000 9.396926208E-0001 1.59E-0011

36 72.0000 9.510565163E-0001 2.46E-0011

37 74.0000 9.612616960E-0001 3.57E-0011

38 76.0000 9.702957263E-0001 5.28E-0011

39 78.0000 9.781476008E-0001 7.80E-0011

40 80.0000 9.848077530E-0001 7.54E-0013

41 82.0000 9.902680687E-0001 1.54E-0012

42 84.0000 9.945218954E-0001 2.14E-0012

43 86.0000 9.975640503E-0001 2.71E-0012

44 88.0000 9.993908270E-0001 4.72E-0012

45 90.0000 1.000000000E+0000 6.37E-0012

1.8. Obliczanie wartości funkcji uwikłanych

Podstawą wielu efektywnych algorytmów numerycznych jest obliczanie ciągu liczb, zbieżnego do poszukiwanej wartości. Proces obliczeniowy polegający na wykonywaniu zespołu działań niezbędnych do wyznaczenia przybliżenia wyższego na podstawie znajomości przybliżenia niższego nazywa się metodą kolejnych przybliżeń lub metodą iteracji.

Jedną z najbardziej znanych metod iteracyjnych jest metoda stycznych, nazywana najczęściej metodą Newtona. Metodę tę zastosujemy do obliczania wartości funkcji uwikłanej, określonej równaniem

(1.42)

Założymy, że zarówno funkcja
jak i jej pochodna
są ciągłe.

Ciąg kolejnych przybliżeń metody stycznych Newtona napiszemy rozpatrując wykres funkcji (rys. 1.3)

(1.43)

w której x pełni rolę parametru. Oznaczając przez przybliżoną wartość nieznanej funkcji y, na podstawie rysunku 1.3 uzyskujemy zależność

pozwalającą na obliczenie jej nowego przybliżenia

. (1.44)

Uogólniając to postępowanie otrzymujemy wzór określający metodę stycznych New-tona

(n = 0, 1, 2, ...), (1.45)

w którym
jest zadanym przybliżeniem początkowym.

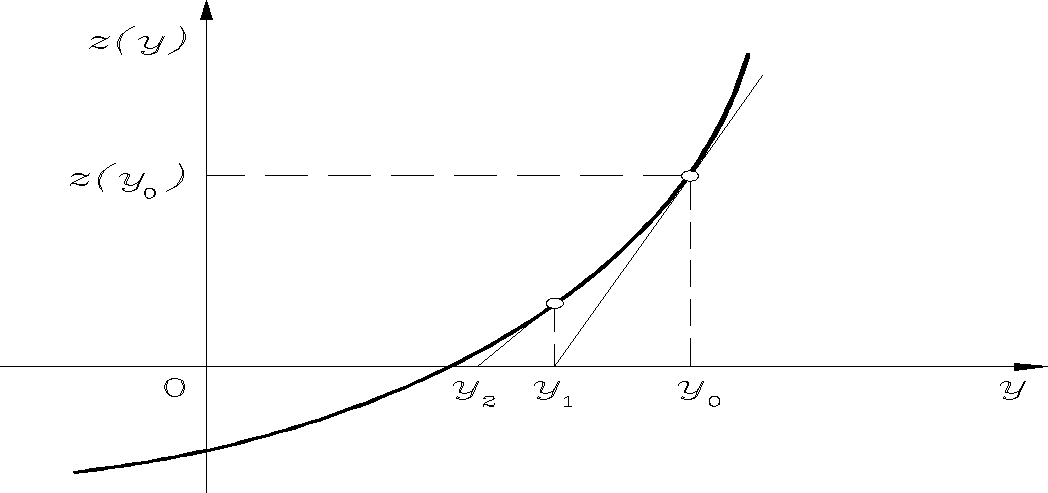
Rys. 1.3

Przerwanie obliczeń następuje w chwili, gdy dwa kolejne przybliżenia spełniają nierówność

(1.46)

gdzie ε jest żądaną dokładnością obliczeń - co gwarantuje na ogół, że również jest

gdyż ciągi konstruowane w metodzie Newtona są bardzo szybkozbieżne i błędy zaokrągleń mają niewielki wpływ na przebieg obliczeń. Proces iteracyjny jest zbieżny, jeżeli pochodne
oraz
istnieją i nie zmieniają znaku w przedziale zawierającym nieznaną wartość funkcji y i jej przybliżenie początkowe
.

Metodę Newtona (1.43) ÷ (1.46) zastosujemy obecnie do wyznaczenia wartości funkcji

(1.47)

Przyjmując funkcję (1.42) w postaci

(1.48)

po obliczeniu pochodnej

(1.49)

i wykorzystaniu wzoru (1.45)

ostatecznie uzyskujemy następujący ciąg kolejnych przybliżeń

(1.50)

Z założenia: x > 0 wynika, że musi być również
przyjmiemy

(1.51)

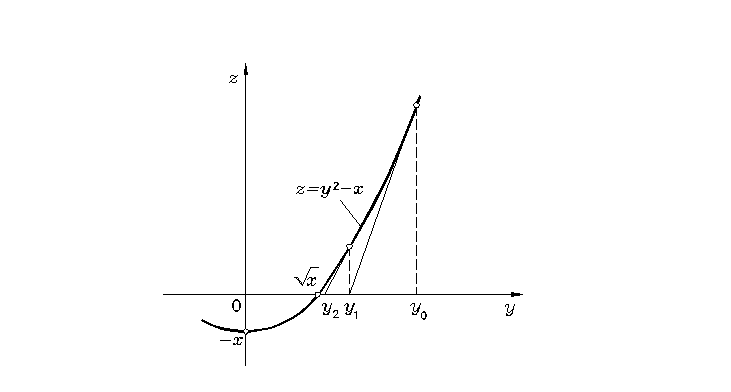
Rys. 1.4

W przypadku obliczania pierwiastka kwadratowego ze wzorów (1.47) ÷ (1.49), ciąg kolejnych przybliżeń (1.50) dla m = 2

nazywa się procesem Herona; geometryczną interpretację metody Newtona, zastosowanej do funkcji
przedstawia rysunek 1.4.

Wyznaczanie wartości funkcji (1.47) przy wykorzystaniu ciągu kolejnych przybliżeń (1.50) ÷ (1.51) jest realizowane w programie 1.5. Obliczona z zadaną dokładnością (1.46) wartość funkcji (1.47) jest porównywana z wartością tej funkcji, uzyskaną poprzez wywołanie funkcji standardowych.

Tabulogram modułu Obliczenia programu 1.5:

{Program 1.5}

unit Obliczenia;

interface

uses

Windows, Messages, SysUtils, Classes, Graphics, Controls,

Forms, Dialogs, StdCtrls, Buttons;

. . . . . . . . . . . . . . . . .

var

Form3: TForm3;

bl,eps,x,y,y1: Double;

iter,m: Integer;

plik: Text;

implementation

uses Ustawienia, Informacje, Grafika, Podglad;

. . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn1Click(Sender: TObject);

label kon;

begin

Form2.Show;

AssignFile(plik,Edit4.Text);

Rewrite(plik); Writeln(plik,'PROGRAM 1.5.');

Writeln(plik,'Obliczanie pierwiastka arytmetycznego.');

Writeln(plik,'Metoda Newtona.');

Writeln(plik,'');

x:=StrToFloat(Edit1.Text);

Writeln(plik,'Argument (x>0) - x = ',x:13);

m:=StrToInt(Edit2.Text);

Writeln(plik,'Stopień pierwiastka - m = ',m);

eps:=StrToFloat(Edit3.Text);

Writeln(plik,'Dokładność obliczeń - eps = ',eps:6);

if x<=0 then begin

Form2.Wyniki.Font.Size:=22;

Form2.Wyniki.Font.Color:=clRed;

Form2.Wyniki.Lines.Text:='Pierwiastek z liczby ujemnej

nie istnieje';

goto kon;

end;

y:=x; iter:=0;

repeat

y1:=((m-1)*y+x*Exp((1-m)*Ln(y)))/m;

bl:=Abs(y-y1); y:=y1;

iter:=iter+1;

until bl<eps;

Writeln(plik,'');

bl:=Abs(y-Exp(1*Ln(x)/m));

Writeln(plik,'Wartość pierwiastka: ',y:20);

Writeln(plik,'Błąd pierwiastka: ',bl:11);

Writeln(plik,'Liczba iteracji: ',iter);

kon:

CloseFile(plik);

Form2.Wyniki.Lines.LoadFromFile(Edit4.Text);

end;

. . . . . . . . . . . . . . . . . . . . . . .

procedure TForm3.BitBtn3Click(Sender: TObject);

begin

Close;

end;

end.

Kopie przykładowych wydruków komputerowych ukazujących się na ekranie monitora w formularzu Obliczenia są prezentowane na rysunkach 1.5 ÷ 1.7.

W tablicy 1.2 zamieszczone zostały wyniki dotyczące obliczania pierwiastków arytmetycznych dla x = 2, 3, 4; przyjęto

Rys. 1.5

Rys. 1.6

Rys. 1.7

40 1. Wprowadzenie do metod numerycznych

1.8. Obliczanie wartości funkcji uwikłanych 41

---