Wpływ wspólnego jonu na dysocjację słabego elektrolitu. Roztwory buforowe.

Wpływ wspólnego jonu na dysocjację elektrolitu

Dysocjacja elektrolityczna - proces odwracalny w układzie homogenicznym (ciekłym)

(za wyjątkiem elektrolitów mocnych)

a A + b B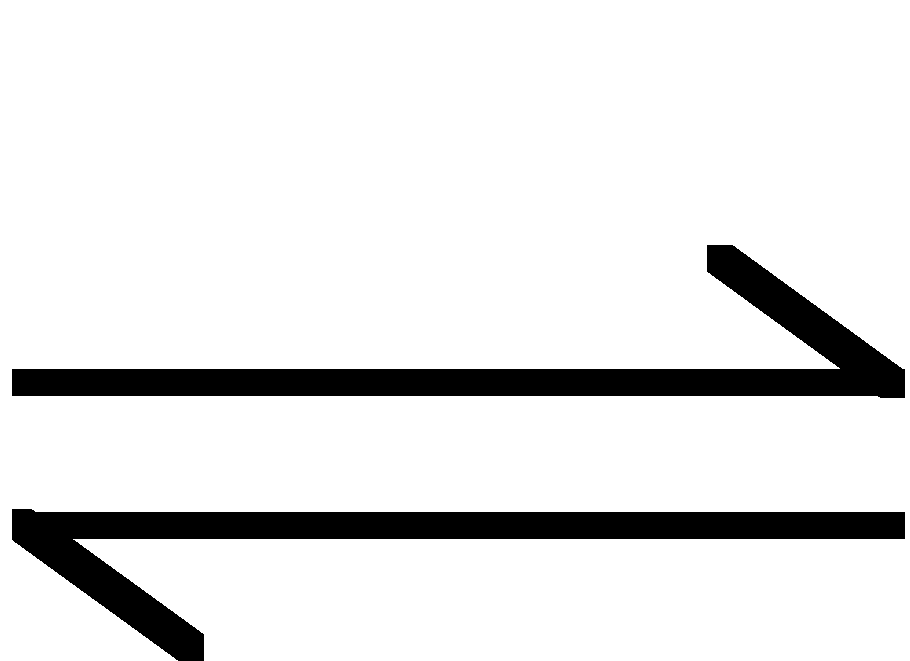
c C + d D

czyli:

- prawo działania mas:

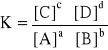
tzn. można:

- rozważać zmiany położenia stanu równowagi wynikające ze zmiany stężenia któregokolwiek ze składników reakcji,

- wyznaczać stężenia składników układu, po wprowadzeniu do roztworów jonów wspólnych z jonami słabego elektrolitu

Cztery przypadki:

1) słaby elektrolit + mocny elektrolit o wspólnym anionie,

a) słaba zasada + mocna zasada, np.:

NH₃ + NaOH

NH₃ + H₂O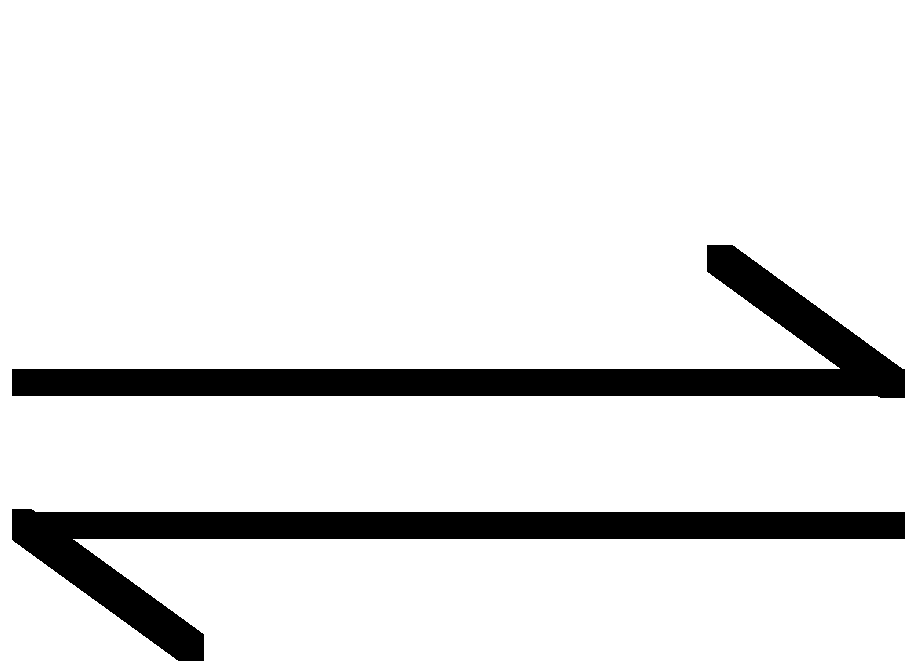

+

NaOH

+

- wspólny jon:

b) słaby kwas + sól tego kwasu (z mocną zasadą), np.:

CH₃COOH + CH₃COONa

CH₃COOH + H₂O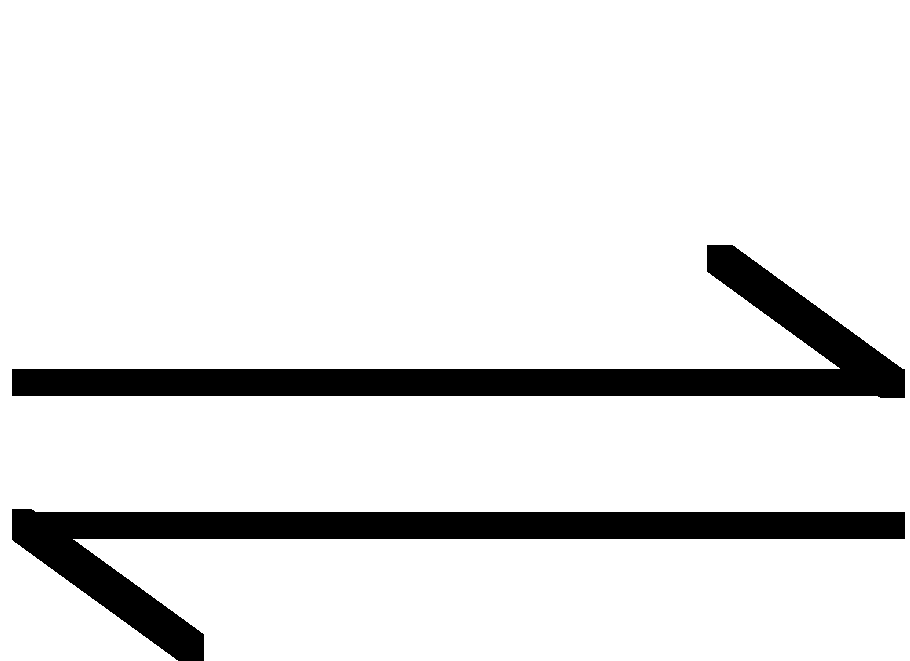

+

CH₃COONa

+

- wspólny jon:

2) słaby elektrolit + mocny elektrolit o wspólnym kationie,

a) słaby kwas + mocny kwas, np.:

HCOOH + HCl

HCOOH + H₂O

+

HCl + H₂O

+

- wspólny jon:

b) słaba zasada + sól tej zasady (z mocnym kwasem), np.:

NH₃ + NH₄NO₃

NH₃ + H₂O

+

NH₄NO₃

+

- wspólny jon:

3) słaby elektrolit + słaby elektrolit o wspólnym kationie,

np. mieszanina dwóch słabych kwasów:

HCOOH + CH₃COOH

HCOOH + H₂O

+

CH₃COOH + H₂O

+

- wspólny jon:

4) słaby elektrolit + słaby elektrolit o wspólnym anionie,

np. mieszanina dwóch słabych zasad:

NH₃ + C₂H₅NH₂

NH₃ + H₂O

+

C₂H₅NH₂ + H₂O

+

- wspólny jon:

Przypadki 1) i 2):

- stan równowagi charakteryzuje jedno wyrażenie określające stałą dysocjacji słabego elektrolitu,

- dodanie wspólnego jonu - cofnięcie dysocjacji słabego elektrolitu

Przypadki 3) i 4):

- stan równowagi charakteryzują dwa wyrażenia, określające stałe dysocjacji słabych elektrolitów,

- wypadkowe stężenie wspólnego kationu lub anionu jest równe sumie stężeń jonów pochodzących od jednego i drugiego słabego elektrolitu.

ad 1a) i 2a)

Do roztworu słabego kwasu HA (K_a), o stężeniu początkowym C₁, dodano mocny kwas HA₁ w takiej ilości, że jego stężenie w roztworze wynosi C₂

- dysocjacja słabego kwasu:

HA + H₂O

+

- dysocjacja mocnego kwasu:

HA₁

+

- stała dysocjacji słabego kwasu:

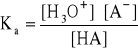
- wprowadzając następujące oznaczenia:

C₁ - początkowe stężenie słabego kwasu HA

C₂ - stężenie mocnego kwasu HA₁

- stężenie jonów
pochodzących z dysocjacji mocnego kwasu

x - stężenie jonów
pochodzących z dysocjacji słabego kwasu

- stężenie anionów
, pochodzących z dysocjacji słabego kwasu

C₁ - x - stężenie niezdysocjowanych cząsteczek słabego kwasu HA₁

zatem:

ad 1b) i 2b)

Do roztworu słabego kwasu HA (K_a), o stężeniu początkowym C₁, dodano roztwór jego soli (MA) w takiej ilości, że jego stężenie wynosi C₂.

- dysocjacja słabego kwasu:

HA + H₂O

+

- dysocjacja soli:

MA

+

- stała dysocjacji słabego kwasu:

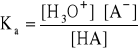
- wprowadzając następujące oznaczenia:

C₁ - początkowe stężenie słabego kwasu HA

C₂ - stężenie soli MA

- stężenie jonów
pochodzących z dysocjacji soli

x - stężenie jonów
pochodzących z dysocjacji słabego kwasu HA

- stężenie jonów
pochodzących z dysocjacji słabego kwasu HA

C₁-x - stężenie niezdysocjowanych cząstek słabego kwasu HA

C₂+x - całkowite stężenie jonów

- w roztworze słabego kwasu:

ponieważ C₂ >> x to C₂ + x = C₂

i C₁ >> x to C₁ - x = C₁

- zatem:

W roztworze będącym mieszaniną słabego kwasu i jego soli (z mocną zasadą) stężenie jonów oksoniowych jest wprost proporcjonalne do stosunku stężenia słabego kwasu do stężenia soli.

Analogicznie:

- w roztworze stanowiącym mieszaninę słabej zasady i jej soli (z mocnym kwasem) stężenie jonów wodorotlenowych jest wprost proporcjonalne do stosunku stężenia słabej zasady do stężenia jej soli:

np.: mieszanina NH₃ - stężenie C₁

i NH₄Cl - stężenie C₂

Przykład 1. Obliczyć zmianę stężenia jonów oksoniowych, jeżeli do 1 dm³ 0,2 molowego roztworu kwasu octowego wprowadzi się 0,5 mola octanu sodu (bez zmiany objętości).

K_a = 1,8

- dysocjacja kwasu octowego:

CH₃COOH + H₂O

+

Stężenie jonów [
]w 0,2 molowym roztworze CH₃COOH:

=

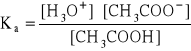
mol/dm³

Stężenie [
] po dodaniu 0,5 mola CH₃COONa:

roztwór staje się także 0,5 molowy względem CH₃COONa,

- przyjmując następujące oznaczenia:

C₁ - początkowe stężenie CH₃COOH

C₂ - stężenie octanu sodu (mocny elektrolit)

- stężenie jonów
pochodzących z dysocjacji soli

x - stężenie jonów
pochodzących z dysocjacji kwasu

- stężenie jonów
pochodzących z dysocjacji kwasu

C₂+x - całkowite stężenie jonów

C₁-x - stężenie niezdysocjowanych cząstek CH₃COOH

- stała dysocjacji kwasu wyraża się zależnością:

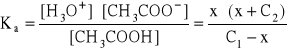
- ponieważ: C₂ >> x i C₁ >> x

to można uznać: C₂ + x C₂ i C₁ - x C₁

- zatem:

- skąd:

mol/dm³

Stężenie jonów oksoniowych zmalało - dodatek wspólnego jonu cofa dysocjację słabego elektrolitu.

Roztwory buforowe

Układy (roztwory):

- niwelujące zmiany pH wynikające z rozcieńczenia roztworu,

- minimalizujące zmiany pH wynikające z dodatku niewielkiej ilości mocnego kwasu lub mocnej zasady.

Zatem, cechy charakterystyczne roztworów buforowych:

- stałe stężenie jonów oksoniowych podczas rozcieńczania,

- bardzo mała zmiana stężenia jonów oksoniowych po dodaniu niewielkiej ilości mocnego kwasu lub mocnej zasady.

Znaczenie roztworów buforowych:

- procesy biochemiczne zachodzące w organizmach roślinnych i zwierzęcych,

- chemia analityczna,

- procesy technologiczne.

Roztwory buforowe:

- mieszaniny słabych kwasów i ich soli (z mocnymi zasadami) lub mieszaniny wodorosoli, np.:

HCOOH + HCOONa

CH₃COOH + CH₃COONa

KH₂PO₄ + Na₂HPO₄

wg teorii Brnsteda-Lowry'ego - roztwory słabych kwasów i sprzężonych z nimi zasad, np.:

HCOOH +

CH₃COOH +

- mieszaniny słabych zasad i ich soli (z mocnymi kwasami), np.:

NH₃H₂O + NH₄Cl

wg teorii Brnsteda-Lowry'ego - roztwory słabych zasad i sprzężonych z nimi kwasów, np.:

Po zmieszaniu dwu roztworów:

1. słabego kwasu HA,

2. sprzężonej z nim zasady
,

w mieszaninie ustala się stan równowagi:

HA + H₂O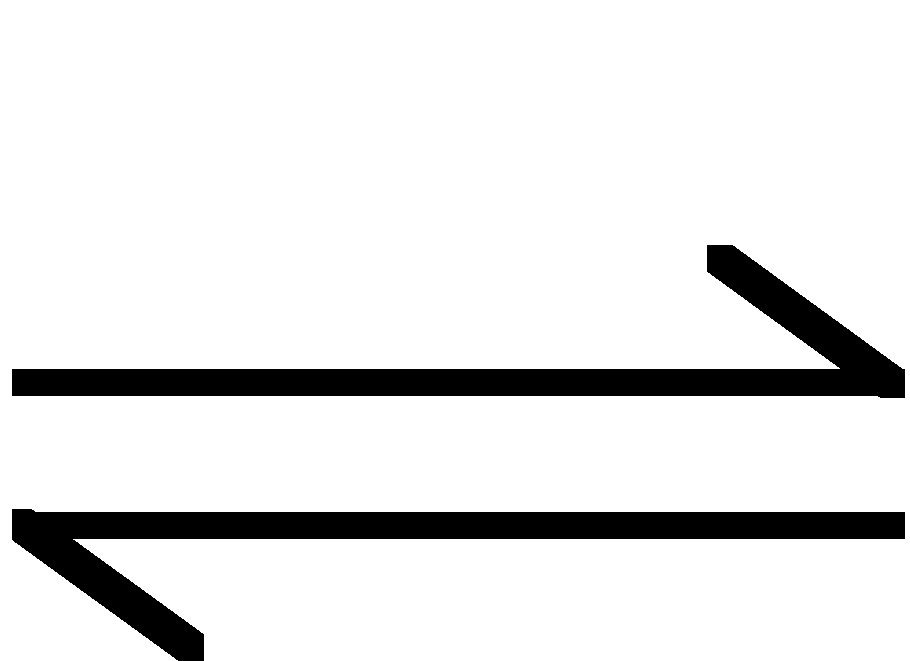

+

Stała równowagi tej reakcji jest stałą dysocjacji kwasowej:

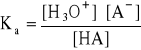
skąd:

czyli:

stężenie jonów hydroniowych zależy od stosunku stężenia kwasu do stężenia sprzężonej z nim zasady,

a wartość pH takiego roztworu:

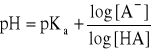
np.:

sprzężona para: kwas - zasada z nim sprzężona

CH3COOH - jony

[HA] = [CH₃COOH] - stężenie kwasu octowego

stężenie początkowe kwasu octowego

[A-] =  stężenie zasady sprzężonej z kwasem octowym, tzn stężenie jonów

=  stężenie soli (np. octanu sodu)

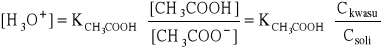
Po zmieszaniu dwu roztworów:

1. słabej zasady BOH,

2. sprzężonego z nią kwasu
,

w mieszaninie ustala się stan równowagi:

BOH + H2O

H₂O +

Stała równowagi tej reakcji jest stałą dysocjacji zasadowej:

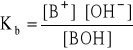
skąd:

czyli:

stężenie jonów wodorotlenowych zależy od stosunku stężenia zasady do stężenia sprzężonego z nią kwasu,

a wartość pOH takiego roztworu:

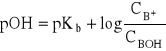
skąd:

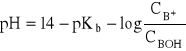
np.:

sprzężona para: zasada - sprzężony z nią kwas

-

(np. chlorek amonu)

  
   
+

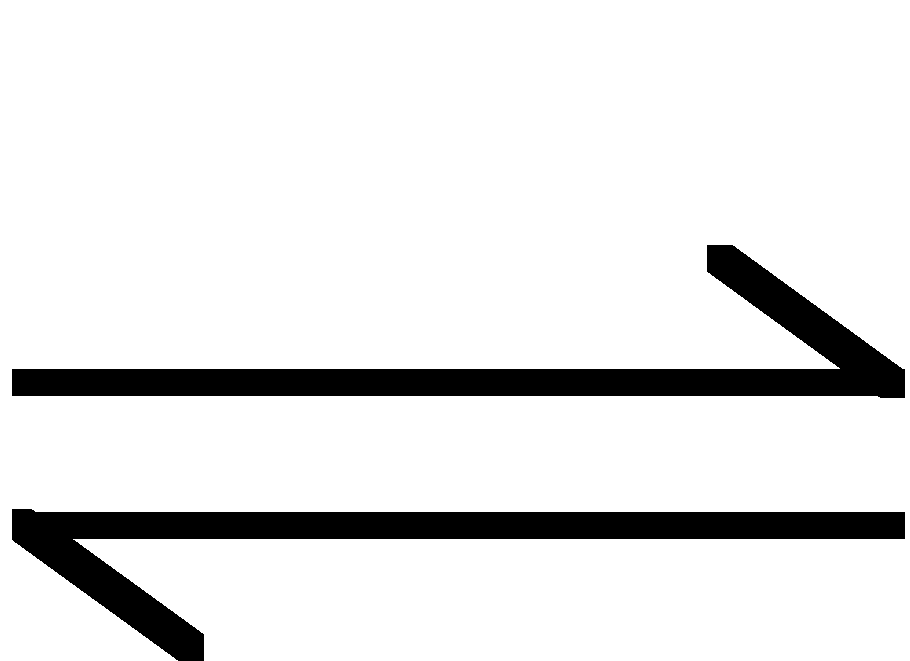
[BOH] = [NH₃] - stężenie amoniaku

stężenie początkowe amoniaku

[B⁺] =  stężenie kwasu sprzężonego z amoniakiem, tzn. stężenie jonów

=  stężenie soli (np. chlorku amonu)

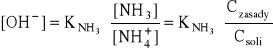
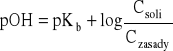
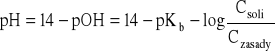
Obecnie

- roztwór zawierający amoniak i sól amonową traktuje się jak roztwór kwasu i sprzężonej z nim zasady:

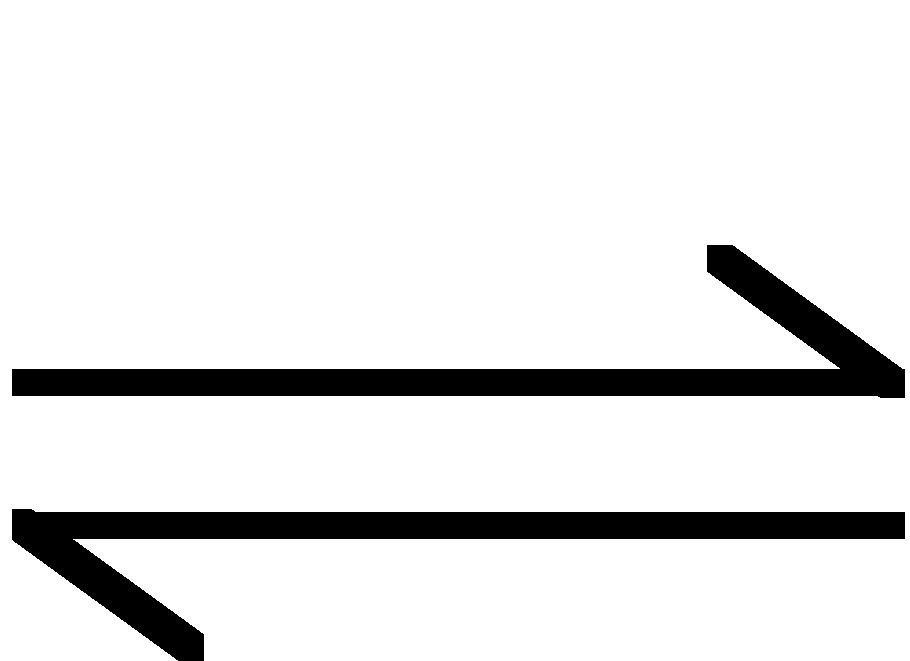
  NH₃ +

Stała równowagi tej reakcji jest stałą dysocjacji kwasowej jonu amonowego:

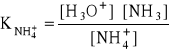
skąd:

- uwzględniając:

KaKb = Kw = 10-14

czyli:

i

- otrzymuje się wyrażenie wyprowadzone poprzednio:

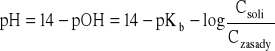
Przykład 2. Obliczyć zmianę pH w 110^-4 molowym roztworze HCl po dodaniu 0,01 mola HCl (bez zmiany objętości roztworu).

- HCl - mocny elektrolit:

HCl + H₂O
+

- [H₃O⁺] przed dodaniem kwasu:

[H₃O⁺] = C_HCl = 110^-4

pH = 4

- całkowite stężenie kwasu po dodaniu 0,01 mola HCl:

=

- [H₃O⁺] po dodaniu kwasu:

[
]' = 110^-2

pH = 2

Przykład 3. Obliczyć stężenie jonów oksoniowych i pH roztworu buforowego, zawierającego w objętości 0,5 dm3:

- 4,6 g kwasu mrówkowego (HCOOH) i

17,0 g mrówczanu sodu (HCOONa).

K_a = 2,510^-4 pK_a = 3,60

- stężenie jonów
w roztworze buforowym:

- pH roztworu buforowego:

skąd:

pH = -log [H₃O⁺] = 4

lub:

Przykład 4. Obliczyć zmianę pH roztworu buforowego z przykładu 2., po dodaniu 0,01 mola HCl (bez zmiany objętości roztworu).

- w roztworze buforowym:

- skutkiem reakcji kwasu (jonów [
]) z zasadą (jonami
) tworzy się niezdysocjowany kwas HCOOH,

- zatem całkowite stężenie kwasu [HCOOH]' wyniesie:

[HCOOH]' = 0,2 + 0,01 = 0,21 mol/dm³

- stężenie jonów [
] zmniejszy się o tyle, o ile wzrośnie stężenie kwasu,

- czyli stężenie zasady (jonów
):

[
]' = 0,5 - 0,01 = 0,49 mol/dm³

- zatem pH roztworu buforowego po dodaniu kwasu:

Przykład 5. Do kolby miarowej pojemności 1 dm³ wprowadzono 10,0 cm³ roztworu amoniaku o stężeniu 8,84% i gęstości 0,964 g/cm³ oraz 4,279 g stałego chlorku amonu. Zawartość kolby rozcieńczono wodą do objętości 1 dm³. Obliczyć pH otrzymanego roztworu buforowego.

K_amoniaku = 1,8·10^-5

W roztworze znajdują się jony wynikające z dysocjacji:

a) chlorku amonu:

b) amoniaku:

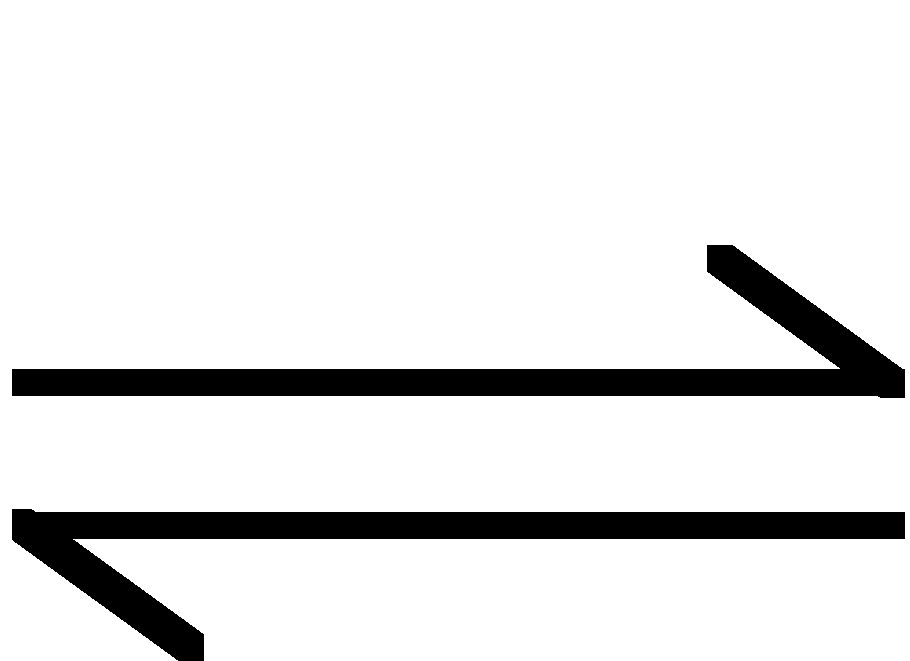
- równowaga w tym roztworze: równowaga dysocjacji zasadowej amoniaku,

- zatem:

- pH tego roztworu (zasadowego) oblicza się wg zależności:

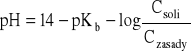
- konieczne jest jednak uprzednie obliczenie stężeń molowych soli i zasady w otrzymanym roztworze:

a) stężenie amoniaku:

masa amoniaku w roztworze wyjściowym:

stężenie molowe amoniaku w roztworze utworzonym:

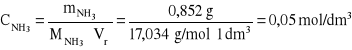
b) stężenie molowe chlorku amonu:

- pH roztworu buforowego:

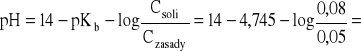
14 - 4,745 - 0,204 = 9,051

Inne podejście do obliczeń:

- równowaga w tym roztworze: równowaga dysocjacji kwasowej, przy czym kwasem są jony amonowe:

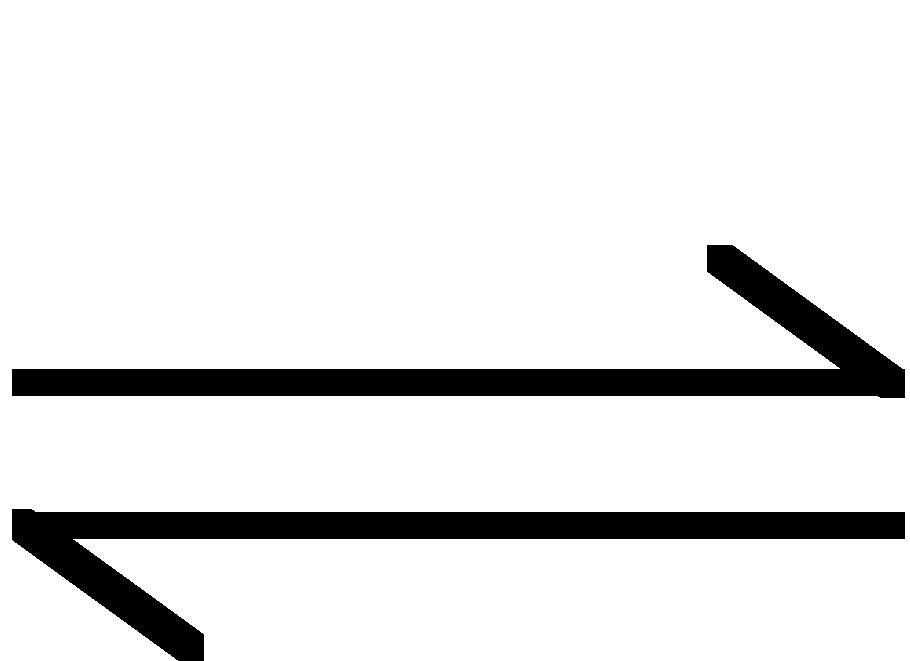
- przy obliczaniu pH korzysta się z zależności:

skąd:

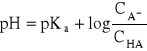
gdzie:

K_a - stała dysocjacji kwasu sprzężonego z zasadą NH₃, czyli stała dysocjacji kwasowej jonów amonowych,

- stężenie zasady sprzężonej, czyli stężenie NH3,

C_HA - stężenie kwasu, czyli stężenie jonów amonowych.

- znając: K_b = 1,810^-5

- i wiedząc, że: K_aK_b = K_w

- oblicza się K_a:

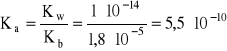
- a stąd:

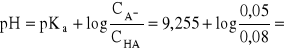
Zadania

 1. W 1,0 dm³ roztworu zawarte jest 0,2 mola kwasu azotowego(III) i 0,02 mola kwasu chlorowodorowego. Obliczyć stężenie jonów azotanowych(III) w tym roztworze.

K_kwasu = 4·10^-4

 2. Do 0,5 dm³ 0,2 molowego roztworu amoniaku dodano 0,5 dm³ 0,02 molowego roztworu wodorotlenku sodu. Obliczyć stężenie jonów amonowych w powstałym roztworze.

K_amoniaku = 1,810^-5

 3. Zmieszano 0,5 dm³ 0,02 molowego roztworu kwasu chlorowego(I) i 0,5 dm³ 0,2 molowego roztworu chloranu(I) sodu. Obliczyć stężenie jonów oksoniowych w powstałym roztworze.

K_kwasu = 4,310^-8

 4. W 1,0 dm³ roztworu zawarte jest 0,3 mola amoniaku i 0,02 mola chlorku amonu. Obliczyć stężenie jonów wodorotlenowych w tym roztworze.

K_amoniaku = 1,810^-5

 5. W 0,5 dm³ roztworu zawarte jest 0,02 mola jednoprotonowego słabego kwasu (HA) i 0,2 mola soli sodowej tego kwasu (NaA). Obliczyć stężenie jonów oksoniowych w tym roztworze.

K_HA = 7,210^-8

 6. W 0,5 dm³ roztworu zawarte jest 0,2 mola jednoprotonowej słabej zasady (BOH) i 0,02 mola chlorku tej zasady (BCl). Obliczyć stężenie jonów wodorotlenowych w tym roztworze.

K_BOH = 510^-4

 7. Obliczyć pH 0,2 molowego roztworu kwasu octowego, do którego dodano octan sodu w takiej ilości, że stężenie soli = 0,05 mol/dm³.

K_kwasu = 1,8·10^-5

 8. Obliczyć stężenie jonów azotanowych(III) w:

a) 0,5 molowym roztworze kwasu azotowego(III) K_kwasu = 4·10^-4

b) po dodaniu 0,2 mola HCl (bez zmiany objętości).

 9. Obliczyć pH roztworu zawierającego w objętości 1 dm³: 0,1 mola amoniaku i 0,2 mola chlorku amonu.

K_amoniaku = 1,8·10^-5

10. Obliczyć stężenie jonów oksoniowych w roztworze, zawierającym w objętości 0,5 dm³ 0,1 mola kwasu octowego i 0,1 mola octanu potasu.

K_kwasu = 1,8·10^-5

11. 21,4 g chlorku amonu rozpuszczono w 1 dm³ roztworu amoniaku o stężeniu 0,21 mol/dm³. Obliczyć pH w powstałym roztworze.

K_amoniaku = 1,8·10^-5

12. Obliczyć masę octanu sodu, którą należy rozpuścić w 500 cm³ 0,2 molowego roztworu kwasu octowego, aby otrzymać roztwór buforowy o pH = 5. Założyć, że rozpuszczenie soli nie spowoduje zmiany objętości roztworu.

K_kwasu = 1,8·10^-5

13. Do 1 dm³ roztworu buforowego, w którym stężenie chlorku amonu = 1,2·10^-3 mol/dm³, a pH = 9,7 dodano 100 cm³ 1,0 molowego roztworu amoniaku. Obliczyć pH powstałego roztworu.

K_amoniaku = 1,8·10^-5

14. Do kolby miarowej poj. 1 dm³ wprowadzono 100 cm³ 1,0 molowego roztworu amoniaku i 100 cm³ 1,0 molowego roztworu chlorku amonu, po czym całość uzupełniono wodą do objętości 1 dm³. Obliczyć pH w powstałym roztworze.

K_amoniaku = 1,8·10^-5

15. Jak zmieni się pH roztworu z poprzedniego zadania, jeżeli do roztworu wprowadzi się 0,01 mola HCl (bez zmiany objętości)?

16. Obliczyć stężenie jonów oksoniowych i pH w roztworze buforowym, zawierającym w objętości 500 cm³ 0,25 g kwasu mrówkowego i 0,25 g mrówczanu potasu.

K_kwasu = 1,8·10^-4

17. Obliczyć wykładnik stężenia jonów oksoniowych w roztworze buforowym powstałym ze zmieszania 2 objętości 1,00% roztworu amoniaku i 8 objętości 1,00% roztworu bromku amonu. Gęstość wszystkich roztworów przyjąć = 1,0 g/cm³.

K_amoniaku = 1,8·10^-5

18. Do 200 cm³ 0,2 molowego roztworu kwasu octowego dodano 180 cm³ 0,2 molowego roztworu wodorotlenku sodu. Obliczyć pH w otrzymanym roztworze.

K_kwasu = 1,8·10^-5

19. Który roztwór wykazuje większą kwasowość:

a) 0,01 molowy HClO

b) mieszanina zawierająca w objętości 1 dm³: 0,01 mola HClO i 0,01 mola KClO

K_kwasu = 4,3·10^-7.

20. Należy przygotować roztwór buforowy złożony z kwasu octowego i octanu sodu, o pH = 4. Sumaryczne stężenie molowe obu składników winno być równe 0,2 mol/dm³. Obliczyć stężenie każdego składnika.

K_kwasu = 1,8·10^-5

21. Obliczyć zmianę pH:

a) 0,01 molowego roztworu HCl,

b) 0,01 molowego roztworu HCOOH,

c) roztworu buforowego będącego mieszaniną 0,01 molowego HCOOH i 0,01 molowego HCCOK

po dziesięciokrotnym rozcieńczeniu.

K_kwasu = 1,8·10^-4

22. Obliczyć, w jakim stosunku objętościowym należy zmieszać 0,05 molowy roztwór kwasu mlekowego i 0,5 molowy roztwór mleczanu potasu, aby po uzupełnieniu wodą do objętości 500 cm³ otrzymać roztwór buforowy o pH = 4,5.

K_kwasu = 2,5·10^-4

23. Obliczyć stężenie jonów oksoniowych i wykładnik stężenia jonów oksoniowych w roztworze buforowym składającym się z mieszaniny 0,1 mola diwodoroortofosforanu(V) sodu i 0,1 mola wodoroortofosforanu(V) sodu w jednym decymetrze sześciennym roztworu. Wartość stałej dysocjacji drugiego etapu kwasu ortofosforowego(V) K₂ = 6,2·10^-8.

Rozwiązania

 1. [
] = 2,7·10^-4

 2. [
] = 2·10^-4

 3. [
] = 4,3·10^-9

 4. [
] = 2,7·10^-4

 5. [
] = 7,2·10^-9

 6. [
] = 5·10^-5

 7. pH = 4,14

 8. a) [
] = 1,4·10^-2 b) [
] = 1·10^-3

 9. pH = 8,95

10. [
] = 1,8·10^-5

11. pH = 8,98

12. m_{octanu sodu} = 14,76 g

13. pH = 9,71

14. pH = 9,26

15. pH = 9,18

16. pH = 3,49

17. pH = 9,41

18. pH = 5,7

19. a) pH = 4,19; b) pH = 6,37; większa kwasowość - roztwór a

20. C_kwasu = 0,17 mol/dm³; C_soli = 0,03 mol/dm³

21. a) ΔpH = 1; b) ΔpH = 0,49; c) ΔpH = 0

22. V_kwasu : V_soli = 6 : 5

23. [H₃O⁺] = 6,2·10^-8; pH = 7,21

Mantysy dwucyfrowe logarytmów dziesiętnych

	0	1	2	3	4	5	6	7	8	9
1 2 3 4 5 6 7 8 9	00 30 48 60 70 78 85 90 95	04 32 49 61 71 79 85 91 96	08 34 51 62 72 79 86 91 96	11 36 52 63 72 80 86 92 97	15 38 53 64 73 81 87 92 97	18 40 54 65 74 81 88 93 98	20 41 56 66 75 82 88 93 98	23 43 57 67 76 83 89 94 99	26 45 58 68 76 83 89 94 99	28 46 59 69 77 84 90 95 996

10

11

---