Macierze rzeczywiste, działania

Def:

Zapis:

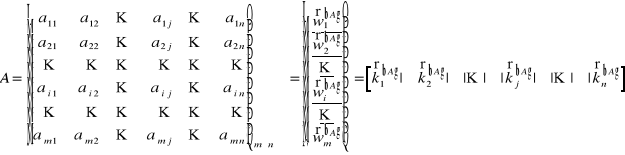
i numeruje wiersz, j numeruje kolumnę, m
n - wymiar macierzy,

- element macierzy znajdujący się na przecięciu i-tego wiersza i j-tej kolumny

Zapis skrócony:
Umowa:

Działania (podstawowe):

DODAWANIE MACIERZY (O TYM SAMYM WYMIARZE) :

,

MNOŻENIE MACIERZY PRZEZ LICZBĘ k :

,

TRANSPONOWANIE MACIERZY:

(zamiana wierszy na kolumny lub odwrotnie)

Zbiór macierzy tego samego wymiaru tworzy grupę ze względu na dodawanie: z elementem neutralnym - macierzą zerową 0 (której wszystkie elementy są równe 0) i macierzą przeciwną do A równą
.

ILOCZYN MACIERZY

1. MNOŻENIE SKALARNE WEKTORÓW
   :

B₁) MNOŻENIE MACIERZY WIERSZOWEJ PRZEZ KOLUMNOWĄ:

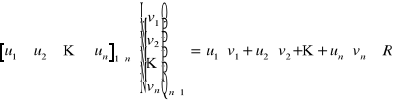
B₂) MNOŻENIE MACIERZY (nie zawsze wykonalne i na ogół nieprzemienne)

(wykonalność mnożenia
: liczba kolumn macierzy wiodącej A = liczbie wierszy macierzy zamykającej B)

(iloczyn macierzy AB jest macierzą C, której elementy otrzymuje się z mnożenia odpowiednich wierszy macierzy A i kolumn macierzy B)

WYZNACZNIK MACIERZY

(definicja permutacyjna, własności, obliczanie)

0) Niech
. Permutacją p zbioru
nazywamy odwzorowanie wzajemnie jednoznaczne (różnowartościowe, na)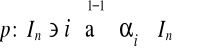
, które zapisujemy

.

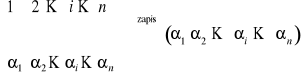
Para
tworzy inwersję (nieporządek) w permutacji p

Permutacja p jest parzysta i piszemy
, gdy liczba wszystkich inwersji p jest liczbą parzystą (tj. 0,2,4, ...).

Permutacja p jest nieparzysta i piszemy
, gdy liczba wszystkich inwersji p jest liczbą nieparzystą (tj. 1,3,5, ...).

Tw. Liczba wszystkich permutacji zbioru
wynosi
, przy czym liczba permutacji parzystych = liczbie permutacji nieparzystych =
.

Zbiór wszystkich permutacji zbioru
tworzy grupę przekształceń (ze względu na superpozycję
) z elementem neutralnym
i elementem odwrotnym do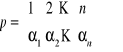
oznaczonym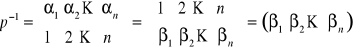
,

(po uporządkowaniu górnego poziomu wg kolejności naturalnej)

przy czym
.

1) definicja permutacyjna wyznacznika macierzy kwadratowej

,

gdzie składnikowi
odpowiada k-ta permutacja zbioru kolumn macierzy A
i

(wyznacznik jest sumą n! iloczynów elementów, po jednym z każdego wiersza i jednym z każdej kolumny, przy czym każdy iloczyn wzięty jest ze znakiem + albo - zależnie od tego, czy permutacja wskaźników kolumn przy uporządkowanych wg wielkości wskaźników wierszy jest parzysta czy nieparzysta)

Wartości wyznacznika z definicji dla:

:
;
:

=

:
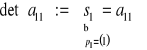
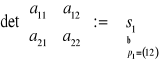
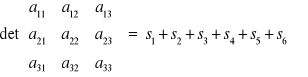
, gdzie

;

;

;

więc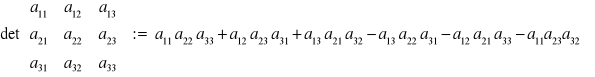
.

Reguła Sarrusa „wychwytuje” sześć składników w definicji przez dopisanie za wyznacznikiem dwóch pierwszych kolumn:
, tj.

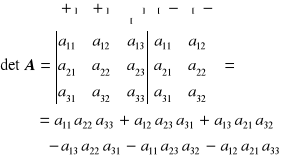
i następnie (patrz powyżej) odpowiedniego mnożenia wzdłuż przekątnych: iloczyny elementów stojących na głównej przekątnej i równoległe do głównej przekątnej są trzema składnikami ze znakiem plus, a pozostałe iloczyny elementów (równoległe do bocznej przekątnej) mają znak minus.

Obliczanie z definicji wyznaczników stopnia
jest uciążliwe, lecz w wielu przypadkach własności wyznaczników pozwalają na znaczne uproszczenia.

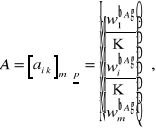
Dla każdej macierzy kwadratowej
stopnia
wprowadzamy macierz dopełnień algebraicznych (zwaną krótko macierzą kofaktorową macierzy A i oznaczaną
):

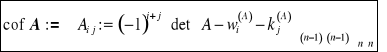
oraz macierz dołączoną macierzy A:
.

Własności wyznaczników i ich efektywne obliczanie

Następujące własności wyznaczników są przydatne do ich obliczania:

W1:
(stąd własność udowodniona dla wierszy jest prawdziwa także dla kolumn i odwrotnie).

W2: Wspólny czynnik danego wiersza (kolumny) można wynieść przed znak wyznacznika (stąd
)

W3: Zamiana miejscami dwóch dowolnych wierszy (kolumn) powoduje zmianę znaku wyznacznika.

W4: Jeśli w macierzy A: istnieje wiersz (kolumna) zerowa (zawierająca same zera) lub istnieją dwa wiersze (kolumny) proporcjonalne (w szczególności identyczne), to
.

Szczególnie ważną własnością jest dokonanie na macierzy A takiej operacji (zwanej elementarną), która nie zmieni wartości jej wyznacznika.

W5. Jeśli do pewnego i-tego wiersza (j-tej kolumny) dodamy inny, ustalony k-ty wiersz,
(k-tą kolumnę,
) zwany wierszem operacyjnym (kolumną operacyjną), pomnożony (pomnożoną) przez dowolną stałą c (różną od zera), to ta operacja (elementarna) nie zmienia wartości wyznacznika, tzn.

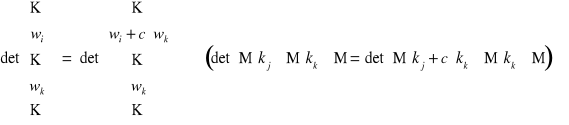
W6.

Rozwinięcie Laplace'a względem i-tego wiersza (r.L.
) :

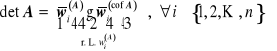
Rozwinięcie Laplace'a względem j-tej kolumny (r.L.
) :

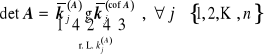
W6'. Uogólnienie: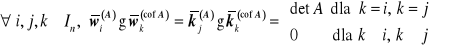
.

Prowadzi to do tożsamości:
.

W7 (Cauchy'ego)

Własność W5 w połączeniu z rozwinięciem Laplace'a W6 pozwala na efektywne obliczanie wyznaczników stopnia
przez sprowadzenie ich do najprostszego wyznacznika stopnia drugiego. Otrzymuje się to przez zastosowanie operacji elementarnych w celu uzyskania jak najwięcej zer w jakimś wierszu (lub kolumnie), a następnie rozwijaniu Laplace'a względem tego wiersza (kolumny).

RZĄD MACIERZY

Definicja rzędu macierzy.

Niech dana będzie macierz
. Tworzymy zbiór wszystkich podmacierzy kwadratowych, uzyskanych przez skreślenie (usunięcie) pewnej ilości wierszy i kolumn w macierzy A (liczba skreślonych kolumn lub wierszy może być równa zeru). Wyznaczniki tych podmacierzy kwadratowych nazywamy minorami.

Rzędem macierzy A (oznaczamy rank A) nazywamy największy stopień różnego od zera minora macierzy A. Dodatkowo przyjmujemy, że rząd macierzy zerowej wynosi 0.

Inaczej możemy powiedzieć: rzędem macierzy
jest liczba
wtedy, gdy istnieje różny od 0 minor stopnia k i wszystkie minory wyższych stopni (jeśli istnieją) są równe 0.

Z definicji wynika np., że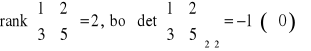
,

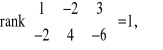
, a wszystkie minory stopnia 2 są równe 0:

.

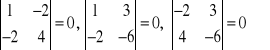
Na uwagę zasługuje własność łącząca rząd macierzy kwadratowej A stopnia n z jej wyznacznikiem i charakteryzująca jej osobliwość lub odwracalność:

.

W praktyce najwygodniej wyznaczać rząd macierzy przez stosowanie operacji na macierzy zachowujących rząd, tzn. takich, które w zastosowaniu do wyznaczników nie powodują zmiany ich wartości z zerowej na niezerową i na odwrót. Wymienione są one w poniższym twierdzeniu.

Twierdzenie (o operacjach zachowujących rząd macierzy). Rząd macierzy nie ulega zmianie, gdy

1. przestawimy wiersze (kolumny); ponadto
   

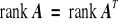
2. dowolny wiersz (kolumnę) pomnożymy przez stałą
   

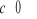
3. do dowolnego wiersza (kolumny) dodamy inny wiersz (kolumnę) pomnożony (pomnożoną) przez stałą
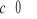
   (operacja elementarna jak we własności W5)

4. skreślimy wiersz (kolumnę) zerową (co powoduje zmianę wymiaru macierzy)

Przykład:

Obliczyć (efektywnie) wyznacznik i rząd macierzy
.

ODWRACANIE MACIERZY KWADRATOWEJ

Tw. Zbiór macierzy kwadratowych stopnia n nieosobliwych (tzn. takich, których wyznacznik jest różny od zera) tworzy grupę nieprzemienną ze względu na mnożenie z elementem neutralnym - macierzą jednostkową I (na głównej przekątnej jedynki, a pozostałe zera) i macierzą odwrotną do macierzy A , oznaczaną przez
i obliczaną wg wzoru

(na podstawie W6':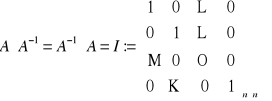
):

SPR.
.

UWAGA: Prawdziwe są własności transponowania i odwracania:

Przykłady :

1) Znaleźć (i sprawdzić) macierz odwrotną do macierzy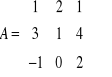
.

2) Rozwiązać równanie macierzowe: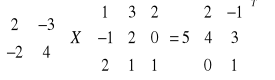
.

Rozwiązanie - szkic

Rachunki:

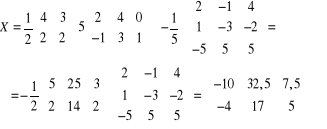
SPR>

8

---