1. definicja wektora
Wektorem nazywamy odcinek prostej, ustalony przez uporządkowaną parę punktów, z których pierwszy jest początkiem wektora, a drugi jest jego końcem. Odległość między początkiem a końcem wektora nazywamy długością wektora.
2. rozkład wektora na składowe
ujęcie graficzne: uzyskujemy przez narysowanie strzałki na płaszczyźnie lub w przestrzeni.
ujęcie analityczne: układ dwóch liczb - współrzędnych (na płaszczyźnie), lub trzech liczb (w przestrzeni)
związek między dwoma ujęciami wektora - strzałką wektora (ujęcie graficzne) i liczbami opisującymi położenie początku i końca strzałki.
Współrzędne wektora otrzymujemy odejmując od współrzędnych końca wektora, współrzędne początku tego wektora.
4. iloczyn skalarny (praca mechaniczna) i wektorowy (moment siły, prędkość kątowa)
Wynikiem mnożenia skalarnego jest liczba (skalar) o wartości równej iloczynowi wartości obu wektorów razy kosinus kąta między nimi zawartego.
Praca jako iloczyn skalarny wektorów siły i przesunięcia
Powyższy zapis: W = F · S · cos (kąta między wektorem siły, a wektorem przesunięcia) - odpowiada dokładnie definicji iloczynu skalarnego dwóch wektorów.
5. pochodna wektora
Pochodna ta stosuje sie do wektorów zmieniajacych sie w czasie. Jesli w przedziale czasu Dt
przyrost wektora r(t) wynosi Dr: Dr = r(t+Dt) - r(t),
7. wektor wodzący-definicja prędkości i przyspieszenia.
Wektor wodzący - dla danego punktu A to wektor zaczepiony w początku układu współrzędnych i o końcu w punkcie A, czyli np. w układzie kartezjańskim:
Wektorowa postać definicji prędkości
kierunek wektora prędkości jest zgodny z kierunkiem przesuwania się ciała, czyli z wektorem S. Wektor prędkości w ruchu prostoliniowym możemy rozumieć jako strzałkę, która łączy położenie początkowe z położeniem w jakim punkt znajdzie się po jednej sekundzie.
Prędkość (liniowa, chwilowa) jest wielkością wektorową definiowaną poprzez stosunek przemieszczenia do (bardzo krótkiego) czasu, w którym to przemieszczenie nastąpiło
Przyspieszenie (liniowe, chwilowe) jest wielkością wektorową definiowaną poprzez stosunek zmiany prędkości do (bardzo krótkiego) czasu, w którym ta zmiana nastąpiła
Prędkość kątowa (chwilowa) jest wielkością wektorową definiowaną poprzez stosunek zakreślonego (skierowanego) kąta do (bardzo krótkiego) czasu, w którym ta zmiana nastąpiła
Przyspieszenie kątowe (chwilowe) jest wielkością wektorową definiowaną poprzez stosunek zmiany prędkości kątowej do (bardzo krótkiego) czasu, w którym ta zmiana nastąpiła
8. Zasady dynamiki Newtona :
I Zasada dynamiki:
Istnieje taki układ odniesienia, w którym
- jeżeli na ciało nie działają siły zewnętrzne, lub działające siły równoważą się, to ciało pozostaje w spoczynku, lub porusza się ruchem jednostajnym prostoliniowym.
II Zasada dynamiki:
Przyspieszenie jakie nadaje niezrównoważona siła F ciału o masie m jest wprost proporcjonalne do tej siły, a odwrotnie proporcjonalne do masy ciała.
III Zasada dynamiki:
Jeżeli ciało A działa na ciało B siłą Fab, to ciało B działa na ciało A siłą Fba, o takim samym kierunku i wartości jak Fab, ale przeciwnym zwrocie
układ inercjalny:
Układ inercjalny - układ odniesienia, względem którego każde ciało niepodlegające zewnętrznemu oddziaływaniu z czymkolwiek porusza się bez przyśpieszenia (tzn. ruchem jednostajnym prostoliniowym); zwany również układem "inercyjnym". Istnienie takiego układu jest postulowane przez pierwszą zasadę dynamiki Newtona.
równania ruchu Newtona
Równanie ruchu - równanie różniczkowe, określające szybkość zmian pewnych wielkości fizycznych (np. prędkości, położenia) jako funkcję aktualnego stanu układu. Przez równanie ruchu najczęściej rozumiemy drugą zasadę dynamiki Newtona, zapisaną w postaci równania różniczkowego.
ruch w jednorodnym polu grawitacyjnym
Rzut ukośny - ruch w jednorodnym polu grawitacyjnym z prędkością początkową o kierunku ukośnym do kierunku pola. Ruch ten odpowiada ruchowi ciała rzuconego pod kątem do poziomu. Za rzut ukośny uznaje się też ruch ciała w kierunku ukośnym do jednorodnego pola elektrycznego.
Rzut ukośmy można rozważać jako ruch składający się z rzutu pionowego w górę oraz ruchu jednostajnego prostoliniowego.
Rzut poziomy - ruch w jednorodnym polu grawitacyjnym z prędkością początkową prostopadłą do pola. Odpowiada ruchowi ciała rzuconego poziomo, z pewnej wysokości, przy przybliżeniu braku oporu ruchu i prędkości znacznie mniejszej od I prędkości kosmicznej. Torem ruchu jest parabola o wierzchołku w punkcie rzutu.
Rzut pionowy - ruch w polu grawitacyjnym Ziemi z prędkością początkową skierowaną pionowo do góry oraz przyjętymi przybliżeniami: pomija się opory ruchu, prędkość rzutu jest na tyle mała, że osiągnięta wysokość jest znacznie mniejsza od promienia ziemi (co pozwala na przyjęcie założenia, że pole grawitacyjne jest jednorodne),
jednostki siły
Niuton Siłę najczęściej wyraża się w niutonach - N. 1 N = 1 kg ∙ m/s2 Jeden niuton jest to siła, która jednemu kilogramowi nadaje przyspieszenie o wartości 1 m/s2.
"Kilogram siła" (1kG - "G" jest tu pisane dużymi litrami). Z definicji miała to być siła, równa ciężarowi ciała o masie 1 kg. Łatwo stąd wywnioskować, że: 1 kG ≈ 9,81 N
1 dyna = 1 kg ∙ cm/s2 A ponieważ 1 m = 100 cm, więc : 1N = 100 dyn.
9. Prawo powszechnego ciążenia :
Siła działająca między każdymi dwoma punktami materialnymi o masach m1 i m2 znajdującymi się w odległości r jest siłą przyciągającą, skierowaną wzdłuż prostej łączącej te punkty.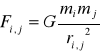
G- stała grawitacyjna, której wartość wynosi:![]()
przyspieszenie ziemskie Przyspieszenie ziemskie - przyspieszenie grawitacyjne ciał swobodnie spadających na Ziemię, bez oporów ruchu. Wartość przyspieszenia ziemskiego zależy od szerokości geograficznej oraz wysokości nad poziomem morza. Przyspieszenie ziemskie normalne (na szerokości geograficznej 45° i poziomie morza) wynosi w przybliżeniu:![]()
definicja 1 kG Jest to masa międzynarodowego wzorca (walca o wysokości i średnicy podstawy 39 mm wykonanego ze stopu platyny z irydem) przechowywanego w Międzynarodowym Biurze Miar . Jest to siła, z jaką Ziemia przyciąga masę 1 kg w miejscu, w którym przyspieszenie ziemskie wynosi 9,80665 m/s2. 1kG=9.81N
10. Dynamika układu punktów materialnych :
równania ruchu
Ruch punktu materialnego jest scharakteryzowany przez kilka parametrów liczbowych (lub wektorów): jego położenie, masę i siłę działającą na niego.
Położenie punktu materialnego jest określane względem wybranego punktu odniesienia (O) znajdującego w przestrzeni. Wybrany punkt wraz z innymi ciałami z nim związanymi nazywamy układem odniesienia.
![]()
środek masy- definicja i przykłady
Środek masy ciała lub układu ciał jest punktem, w którym skupiona jest cała masa w opisie układu jako masy punktowej.
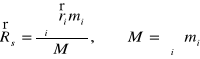
![]()
- wektor wodzący środka masy
Dla ciała znajdującego się w jednorodnym polu grawitacyjnym środek ciężkości pokrywa się ze środkiem masy.
11. Zasada zachowania pędu dla układu punktów materialnych - przykłady
Zasada zachowania pędu. W odniesieniu do pojedynczego punktu materialnego drugą zasadę dynamiki zapisalibyśmy F= dp/∂t. Dla układu punktów materialnych p0 =p1+p2+......
dp0/∂t=dp1/∂t+dp2/∂t+... ![]()
Zasada zachowania pędu dla układu punktów materialnych mówi, że pędy poszczególnych punktów materialnych składających się na ten układ mogą ulegać zmianie, ale całkowity pęd układu pozostaje niezmienny
moment siły i moment pędu
Zasada zachowania pędu Jeżeli na jakiś układ ciał nie działają siły (oddziaływania) zewnętrzne, wtedy układ ten ma stały pęd.
Moment M siły działającej na ciało to wielkość wektorowa określona przez iloczyn wektorowy działającej siły i promienia. Wektor momentu siły jest prostopadły do płaszczyzny wyznaczonej przez wektor siły i wektor r, a jego zwrot określa reguła śruby prawoskrętnej.
Moment pędu L punktu materialnego A o masie m względem punktu O jest definiowany jako iloczyn wektorowy wektora o początku w O a końcu w A i pędu
![]()
siły centralne
Siły centralne skierowane są zawsze wzdłuż promienia wodzącego cząstki - tzn. działają w kierunku punktu, który jest centrum siły (przyciąganie), lub w kierunku przeciwnym (odpychanie). Wartość siły centralnej zależy tylko od odległości od centrum, tzn. . Wiele sił spotykanych w przyrodzie ma charakter siły centralnej, np. siła grawitacji, siła Coulomba, siła sprężystości, siły jądrowe. Ze względu na stałość momentu pędu ruch pod wpływem siły centralnej odbywa się zawsze w jednej płaszczyźnie prostopadłej do wektora .
![]()
12. Prawa Keplera
Pierwsze prawo Keplera stwierdza, że planeta porusza się wokół Słońca po elipsie, w której jednym z ognisk jest Słońce. (O1 * P1) + (O2 * P1) = (O1 * P2) + (O2 * P2) Dla dowolnych P1 i P2, gdzie O to Słońce. Z praw mechaniki wynika, że prawo to jest spełnione w przybliżeniu bardzo dużej masy Słońca.
Drugie prawo Keplera mówi, że w równych jednostkach czasu, promień wodzący planety poprowadzony od Słońca zakreśla równe pola. Wynika stąd, że w peryhelium (w pobliżu Słońca), planeta porusza się szybciej niż w aphelium (daleko od Słońca). Twierdzenie to wynika z zasady zachowania momentu pędu.
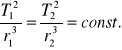
Trzecie prawo Keplera głosi, że stosunek kwadratu okresu obiegu planety wokół Słońca do sześcianu średniej arytmetycznej największego i najmniejszego oddalenia od Słońca jest stały dla wszystkich planet w Układzie Słonecznym
13. Zasada zachowania energii mechanicznej :
Sformułowanie 1 zasady zachowania energii mechanicznej W dowolnym ruchu przebiegającym bez tarcia (i innych strat energii) energia mechaniczna układu izolowanego jest stała. Emechaniczna = const Emechaniczna = Epotencjalna + Ekinetyczna
praca mechaniczna:
Praca mechaniczna to iloczyn wartości siły działającej na ciało zgodnie z przemieszczeniem i wartości przemieszczenia (pod warunkiem, że F = const, ruch prostoliniowy). Jednostką pracy mechanicznej jest 1 J.
![]()
![]()
E=T+V=const
energia kinetyczna i potencjalna
Energią nazywamy zdolność układu do wykonywania pracy. Rozróżniamy energię mechaniczną, cieplną, elektryczną, jądrową. Energię mechaniczną dzielimy na energię potencjalną (wysokości) i kinetyczną (ruchu). Energia potencjalna: Ep = m·g·h Energia kinetyczna: Ek = ½ m·v²
14. Dynamika ciała sztywnego :
ruch obrotowy i postępowy ( 6 st. swobody)
Ruch obrotowy to taki ruch, w którym wszystkie punkty bryły sztywnej poruszają się po okręgach o środkach leżących na jednej prostej zwanej osią obrotu. Np. ruch Ziemi wokół własnej osi. Jest to ruch złożony z ruchu postępowego środka masy danego ciała oraz ruchu obrotowego względem pewnej osi. Środek masy ciała można uważać za punkt materialny. Do opisania ruchu obrotowego używa się odmiennych pojęć od używanych do opisania ruchu postępowego. Ruch postępowy to ruch bryły sztywnej charakteryzujący się tym, że wszystkie punkty ciała przemieszczają się z prędkościami o jednakowych kierunkach, zwrotach i wartościach. Innymi słowy, pole prędkości dla takiego ciała jest jednorodne. Ruch postępowy nie musi odbywać się po linii prostej
związek między prędkością kątową i liniowa ![]()
Pomiędzy prędkością liniową punktu poruszającego się po okręgu, a prędkością kątową istnieje prosta zależność:
![]()
Znaczenie symboli:
ω - prędkość kątowa (w rad/s, lub opuszczając radiany 1/s = s-1)
R - promień okręgu którego fragmentem jest zakreślany łuk (najczęściej w metrach m).
v - prędkość liniowa, czyli „zwykła” prędkość punktu (najczęściej w m/s)
moment pędu bryły w ruchu obrotowym
Rozwa_my obrót ciała wokół ustalonej osi. Dla pojedynczego bardzo małego ciała
(nazywamy go punktem materialnym) moment pedu definiujemy jako: L r p gdzie r jest wektorem położenia punktu materialnego, zas p jest pedem ciała. Moment pedu jest zatem okreslony wzgledem punktu (oznaczonego tutaj jako „0”).
momentem bezwładności
bryły sztywnej względem pewnej osi (definiuje się również inne momenty bezwładności) nazywamy wyrażenie
Aby znaleźć moment bezwładności ciała należy podzielić w myśli to ciało na fragmenty tak małe, aby każdy można było traktować jak punkt materialny o pewnej masie mi, pomnożyć jego masę przez kwadrat jej odlęgłości od osi obrotu ri2 i wszystkie otrzymane iloczyny do siebie dodać. Ta dosyć skomplikowana recepta może być zastoswana praktycznie tylko do ciał, które składają się ze skończonej liczby niewielkich elementów, które można potraktować w przybliżeniu jak zbiór niezależnych punktów materialnych. W praktyce, do ciał rzeczywistych, a więc takich dla których masa jest rozłożona w sposób ciągły stosuje się postać całkową definicji pozwalającą obliczać rzeczywiste momenty bezwładności:
zasady dynamiki Newtona w odniesieniu do bryły sztywnej
Równanie to wyraża zmianę momentu pędu układu w zależności od dziąłającego na nie wypadkowego momentu sił. Przypomnijmy, że moment siły definioowany jest jako iloczyn wektorowy ramienia działania siły i siły
zaś momentu pędu jest definiowany poprzez iloczyny wektorowy wektora wodzącego i pędu
Z II zasady dynamiki (podobnie jak w przypadku ruchu postępowego) można wyprowadzić zasdę zachowania - tym razem momentu pędu. Zauważmy, że jeśli wypadkowy moment sił działających na ciało jest równy zero, to moment pędu jest stały (w czasie). Dla bryły sztywnej (to jest takiej, w której odległości między punkami ją tworzącymi niezmieniają się w czasie ruchu) równanie to można zapisać również w postaci
Energia kinetyczna w ruchu obrotowym
Rozważmy energię kinetyczną ciała, znajdującego się w ruchu obrotowym jednostajnym. Zakładamy, że ciało to ma postać tarczy o masie m i składa się z bardzo dużej ilości elementów o masach m1,m2,...,mn, które są tak małe, że można je przyjąć za punkty materialne. Tarcza ta obraca się dookoła osi przechodzącej przez jej środek ciężkości ze stałą prędkością kątową.
Energia pojedynczego elementu wynosi
15. Drganie harmoniczne proste :
Ruch drgający prosty jest ruchem najczęściej spotykanym w przyrodzie. Przykładami takiego ruchu są: ruch struny instrumentu, ruch ciężarka zawieszonego na sprężynie, ruch wahadła czy ruch tłoka w silniku. Przyczyną tego ruchu jest siła sprężystości.
całkowita energia w ruchu drgającym
W rozważaniach teoretycznych zauważyliśmy, że energia potencjalna i energia kinetyczna wynoszą kolejno
składanie drgań równoległych i prostopadłych
![]()
Ruch drgający tłumiony

16. Ruch falowy : Ośrodek sprężysty ma tę właściwość, ze siłom, które usiłują spowodować jego odkształcenie, przeciwstawia siły sprężyste, które po usunięciu sił odkształcających usuwają odkształcenie. Wytrącenie zespołu cząsteczek takiego ośrodka z położenia równowagi powoduje ich drganie wokół tego położenia, przy czym wskutek jego właściwości sprężystych zaburzenie przenosi się z jednej warstwy ośrodka na następną, wprawiając ją w ruch drgający o takim samym okresie drgań. Takie właśnie przenoszenie drgań nazywamy ruchem falowym lub krótko falą.
Ze względu na czoło fali fale dzielą się na płaskie i kuliste. Jeżeli drgania rozchodzą się w jednym kierunku, to powierzchnie fali są płaszczyznami i mówimy o fali płaskiej. Jeżeli zaś fala wywołana przez punktowe źródło drgań rozchodzi się w ośrodku jednorodnym, to prędkość jej jest jednakowa we wszystkich kierunkach i powierzchnia fali ma postać kuli. Mówimy wtedy o fali kulistej.
Wielkości charakteryzujące falę to:
- amplituda fali
- okres fali
- częstotliwość fali
- prędkość fali (prędkość fali w danym ośrodku jest stała)
- długość fali (odległość między najbliższymi cząsteczkami drgającymi w zgodnych fazach)
Fala przebywa drogę równą swojej długości w czasie okresu.
Zasada Huygensa Każdy punkt ośrodka, do którego dochodzi fala, można traktować jako elementarne źródło wtórnej fali kolistej.
źródła koherentne i interferencja fal Zjawisko nakładania się dwu lub więcej fal harmonicznych harmonicznych tej samej długości, prowadzące do powstania ustalonego w czasie rozkładu przestrzennego obszarów wzmocnienia i osłabienia fali, nazywamy interferencją fal. Jeżeli obie fale będą miały takie same amplitudy to nastąpi maksymalne wzmocnienie. Wygaszenie następuje we wszystkich punktach, dla których różnica odległości od źródeł jest równa nieparzystej wielokrotności połowy długości fali.
interferencja na dwóch szczelinach Dyfrakcją fali nazywamy ugięcie fali, czyli zmianę kierunku rozchodzenia się fali na szczelinach, krawędziach, przeszkodach, itp.
fala stojąca
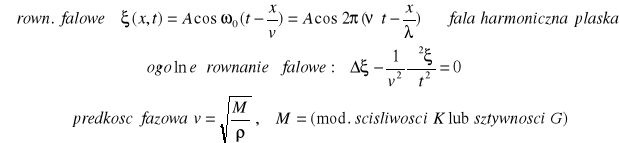
17. Dynamika cieczy
ciecz doskonała, ciecz nieściśliwa, nielepka, inaczej: płyn idealny. Pojęcie to stosuje się w hydrodynamice i aerodynamice do opisu laminarnych przepływów, przy dużych liczbach Reynoldsa.
lepkość cieczy Jeżeli jedną warstwę cieczy (A) o powierzchni P chcemy przesuwać względem drugiej (B) z szybkością względną równą dv a odległość między nimi wynosi dx, to siła F potrzebna do tego będzie wynosić:
Do pomiaru lepkości cieczy służą lepkościomierze (wiskozymetry). Najpopularniejsze to wiskozymetry Ostwalda i Englera, gdzie oblicza się lepkość przez pomiar czasu przepływu badanej cieczy przez rurkę kapilarną, lub wiskozymetr Höplera, w którym mierzy się czas opadania standaryzowanej kulki w przezroczystej rurce napełnionej badaną cieczą.
Równanie Bernoulli'ego Wyodrębniana elementarna objętość cieczy dV o gęstości ρ czyli o elementarnej masie dm posiada określoną energię, która może występować jako energia potencjalna dm·g·z w zależności od wysokości położenia z, jako energia ciśnienia dv·p i jako energia kinetyczna zależna od dm · u2 /2. Zgodnie z prawem zachowania energii całkowita suma energii wyodrębnionej masy cieczy winna być stała, niezależnie od położenia tej masy w przestrzeni. Ta zasada zachowania energii wyrażana jest w postaci równania Bernoulli'ego:

jednostki ciśnienia
![]()
18. Kinetyczno-molekularna teoria gazów:
Gaz doskonały to gaz, który spełnia równanie stanu bez ograniczeń jego parametrów.
podstawowe związki między parametrami makro- i mikroskopowymi
Spoiwem wiążącym ze sobą cząsteczki są siły międzycząsteczkowe, występujące w dwóch postaciach: sił odpychania i sił przyciągania. Odległości między cząsteczkami pary lub gazu są tak duże, że siły przyciągania międzycząsteczkowego praktycznie nie występują, a ruch cieplny tych cząsteczek staje się ruchem postępowym, przy czym cząsteczki zderzają się wzajemnie i rozbiegają w różnych kierunkach zajmując całą dysponowaną objętość. Wynikiem oddziaływania sił międzycząsteczkowych są zderzenia cząsteczek, wskutek czego uzyskują one różne prędkości i kierunki. Jednakże większość z nich porusza się z prędkościami niewiele różniącymi się od wartości średniej, która jest tym większa, im wyższa jest temperatura oraz im mniejsza jest masa cząsteczki.
Od prędkości i odległości miedzy cząsteczkami gazu zależy tzw. droga swobodna, którą przebywa cząsteczka ze stałą prędkością po torze prostoliniowym między dwoma kolejnymi zderzeniami. Mimo, że drogi swobodne poszczególnych cząsteczek różnią się od siebie, to jednak dla większości z nich są bliskie wartości średniej, zwanej średnią drogą swobodną.
19. Termodynamika
pierwsza zasada termodynamiki Zmiana energii wewnętrznej ciała jest równa sumie pracy wykonanej nad ciałem przez siły zewnętrzne i ciepła dostarczonego do ciała.
sformułowanie zasady - mechaniczny równoważnik ciepła
Równoważnik mechaniczny ciepła, stosunek pracy mechanicznej do równoważnej jej ilości ciepła, stosowany, gdy obie te wielkości wyraża się w innych jednostkach, równoważnik mechaniczny ciepła
ciepło właściwe gazu doskonałego
Ciepło właściwe gazów doskonałych nie zależy od temperatury. Jeśli więc ogrzewamy 1 kg gazu o 1°C od temperatury 0°C do 1°C, to musimy dostarczyć tyle samo ciepła, co podczas ogrzewania od 100°C do 101°C. W przypadku gazów rzeczywistych ciepło właściwe (zarówno cp jak i cv) jest zależne od temperatury. Rośnie ono wraz z temperaturą, a więc ogrzewając gaz od 100°C do 101°C musimy dostarczyć więcej ciepła, niż ogrzewając tą samą ilość gazu od 0°C do 1°C.
II zasada termodynamiki określa warunki , jakie muszą być spełnione, by
niesprzeczny z I zasadą proces mógł rzeczywiście zachodzić.
Podstawowymi pojęciami w II zasadzie termodynamiki są: procesy odwracalne
i nieodwracalne
cykl Carnota - ilustracja zasady
Cykl składa się z następujących procesów:
- Sprężanie izotermiczne - czynnik roboczy styka się z chłodnicą, ma temperaturę chłodnicy i zostaje poddany procesowi sprężania w tej temperaturze (T2). Czynnik roboczy oddaje ciepło do chłodnicy.
- Sprężanie adiabatyczne - czynnik roboczy nie wymienia ciepła z otoczeniem, jest poddawany sprężaniu aż uzyska temperaturę źródła ciepła (T1).
- Rozprężanie izotermiczne - czynnik roboczy styka się ze źródłem ciepła, ma jego temperaturę i poddawany jest rozprężaniu izotermicznemu w temperaturze T1, podczas tego cyklu ciepło jest pobierane ze źródła ciepła.
Rozprężanie adiabatyczne - czynnik roboczy nie wymienia ciepła z otoczeniem i jest rozprężany aż czynnik roboczy uzyska temperaturę chłodnicy (T2).
20. Elektryczność i magnetyzm
ładunki elektryczne
Ładunek elektryczny jest wewnętrzną własnością części cząstek elementarnych. Jest wielkością skwantowaną, co oznacza, że każdy ładunek jest całkowitą wielokrotnością ładunku elementarnego, za który uznaje się ładunek elektronu. Rozróżnia się dwa rodzaje ładunków, ładunek elektronu określa się jako ujemny (-1), a protonu dodatni (+1). Ładunki tego samego rodzaju odpychają się, a różnego przyciągają.
prawo Coulomba
Prawo Coulomba głosi, że siła wzajemnego oddziaływania dwóch punktowych ładunków elektrycznych jest wprost proporcjonalna do iloczynu tych ładunków i odwrotnie proporcjonalna do kwadratu odległości między ich środkami. Jest to podstawowe prawo elektrostatyki. Prawo to można przedstawić za pomocą wzoru: ![]()
pole elektryczne - natężenie pola , linie sił pola elektrycznego
Pole elektryczne - pole fizyczne, stan przestrzeni w której na ładunek elektryczny działa siła. Pole to opisuje się przez natężenie pola elektrycznego lub potencjał elektryczny.
wektor indukcji elektrycznej
wektor indukcji elektrycznej jest to wielkość fizyczna wektorowa charakteryzująca pole elektr. wytworzone wewnątrz dielektryka przez swobodne ładunki elektr. Jeżeli pomiędzy okładki kondensatora płaskiego, na których zgromadzone są ładunki swobodne, zostanie wsunięta płytka dielektryka, to pole elektr. między okładkami spowoduje polaryzację dielektryka i powstanie dodatkowego pola elektr., osłabiającego pole ładunków swobodnych. Jednostką i.e. w układzie SI jest kulomb na metr do kwadratu (C/m2).
strumień indukcji i prawo Gaussa dla ładunków elektrycznych
Pole elektryczne jest polem wektorowym, dlatego też zgodnie z twierdzeniem Gaussa-Ostrogradskiego można zdefiniować wielkość zwaną strumieniem natężenia pola: strumień natężenia pola elektrycznego przenikający przez dowolną powierzchnię zamkniętą w jednorodnym środowisku o bezwzględnej przenikalności dielektrycznej ε, jest równy stosunkowi całkowitego ładunku znajdującego się wewnątrz tej powierzchni do wartości tejże przenikalności.
napięcie i potencjał elektryczny
Potencjałem elektrycznym nazywamy iloraz energii potencjalnej punktowego ciała naelektryzowanego ładunkiem q i wartości tego ładunku.
Różnica potencjałów elektrycznych jest nazywana napięciem
Potencjał elektryczny, zwany również elektrostatycznym odpowiada energii potencjalnej ładunku przebywającemu w statycznym polu elektrycznym. Jednostką potencjału elektrycznego jest wolt. Obrazowo, potencjał elektryczny można sobie wyobrażać jako rodzaj "elektrycznego popychadła", przesuwającego ładunek z jednego miejsca w drugie.
prąd elektryczny
Natężenie prądu (nazywane potocznie prądem elektrycznym) jest wielkością fizyczną charakteryzującą przepływ prądu elektrycznego zdefiniowaną jako stosunek ilości ładunku elektrycznego przepływającego przez wyznaczoną powierzchnię do czasu przepływu ładunku.
Wyszukiwarka