Ciała stałe dzielimy na przewodniki, półprzewodniki i dielektryki (izolatory). Przewodnikami są metale. W nich elektrony walencyjne mogą przechodzić na wyższe, niezajęte poziomy. Elektrony w metalach poruszają się swobodnie, dzięki czemu może płynąć prąd. W modelu pasmowym izolatora charakterystyczne jest szerokie pasmo wzbronione, przez które nie przedostają się elektrony i nie może płynąć prąd. W metalach nie ma tego pasma. Półprzewodniki są kompromisem między metalami a dielektrykami. W ich modelu pasmowym również znajduje się pasmo wzbronione, ale jego szerokość jest nieporównywalnie mniejsza i wystarcza niewielka ilość energii, aby elektrony mogły przejść do pasma przewodnictwa.
Tabela 1. Pomiar rezystancji podczas zwiększania temperatury o około co 5 stopni Celsjusza.
Temperatura ustawiona (wskazana) w stopniach Celsjusza |
Oporność rezystora nr 1 (w ) |
Oporność rezystora nr 2 (w ) |
Oporność rezystora nr 3 (w ) |
Oporność rezystora nr 4 (w ) |
23.7 |
110.8 |
51.7 |
70.0 |
119.2 |
25 (26.2) |
111.5 |
48.8 |
65.2 |
110.1 |
30 (32.8) |
112.4 |
42.8 |
57.5 |
97.6 |
35 (38.8) |
113.4 |
38.3 |
51.5 |
86.8 |
40 (42.3) |
113.8 |
36.2 |
48.8 |
82.1 |
45 (46.9) |
115 |
33 |
44.1 |
73.8 |
50 (51.4) |
116.7 |
30.8 |
40.8 |
67.6 |
55 (56.4) |
118 |
28.2 |
37 |
61 |
60 (61.4) |
119.7 |
25.6 |
33.1 |
54.2 |
65 (66.7) |
120.8 |
23.4 |
29.9 |
48.8 |
70 (71.4) |
121.9 |
21.2 |
26.9 |
43.6 |
75 (76.8) |
123.2 |
19.1 |
24 |
38.9 |
80 (81.3) |
124.4 |
17.8 |
22.2 |
35.7 |
85 (85.1) |
125.7 |
16.4 |
20.1 |
32.2 |
90 (91.5) |
127.3 |
15.1 |
18.2 |
29 |
95 (95.2) |
128.4 |
14 |
16.7 |
26.4 |
100 (100.2) |
129.6 |
13.1 |
15.5 |
24.4 |
Tabela 2. Pomiar rezystancji podczas chłodzenia rezystorów za pomocą wentylatora. Pomiar dokonany przy studzeniu o około co 5 stopni Celsjusza.
Temperatura ustawiona (wskazana) w |
Oporność rezystora nr 1 (w ) |
Oporność rezystora nr 2 (w ) |
Oporność rezystora nr 3 (w ) |
Oporność rezystora nr 4 (w ) |
95 (98.8) |
130.7 |
13.7 |
15.9 |
24.6 |
90 (95.3) |
130.3 |
14.2 |
16.7 |
26 |
85 (87) |
129.7 |
15.5 |
18.2 |
28.3 |
80 (81.5) |
127.8 |
16.7 |
20 |
31.5 |
75 (76.6) |
126.1 |
18.2 |
22.1 |
35.2 |
70 (72.1) |
124.7 |
19.6 |
24.1 |
38.7 |
65 (67.3) |
123.3 |
21.3 |
26.6 |
42.9 |
60 (62.1) |
121.8 |
23.1 |
29 |
47.2 |
55 (57.7) |
120.5 |
25.5 |
31.9 |
52.4 |
50 (52.2) |
119.3 |
27.7 |
35.2 |
58.3 |
45 (47.3) |
117.3 |
29.9 |
38.5 |
64.5 |
Wykres 1. Zależność oporności rezystorów od temperatury.
Dla rezystora pierwszego oporność wzrasta wraz ze wzrostem temperatury i spada wraz ze spadkiem. Odwrotnie jest dla innych rezystorów. Rezystor nr 1 jest metalem, a rezystory nr 2,3 i 4 są półprzewodnikami.
Dla metali współczynnikiem zależności oporności od temperatury jest współczynnik temperaturowy.
Współczynnik temperaturowy obliczamy ze wzoru:
![]()
gdzie: opór końcowy
opór w temperaturze 23,7 C
![]()
![]()
K-1
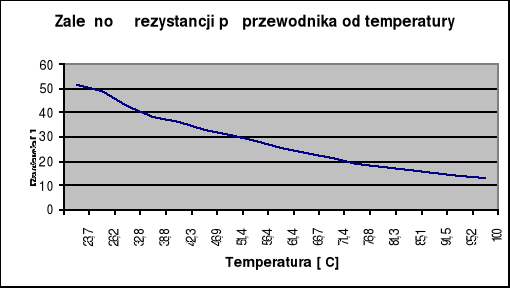
Wykres 2. Zależność rezystancji półprzewodnika od temperatury.
Dla półprzewodników charakterystyczne jest pasmo wzbronione. Szerokość przerwy energetycznej liczymy odpowiednio:
![]()
gdzie k - stała Boltzmanna = 1,38044 x 10^-23
a- współczynnik kierunkowy prostej na wykresie 2
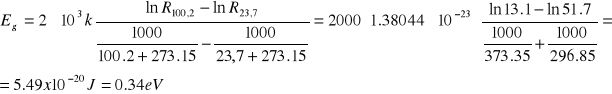
Wnioski: Metale nie mają przerwy energetycznej, a izolatory mają ją bardzo dużą, rzędu 10 eV. Kompromisem pomiędzy nimi są półprzewodniki, które mają przerwę energetyczną mniejszą od 2eV. Nasz półprzewodnik mieści się w tych granicach, a więc przerwa energetyczna została dobrze policzona. Gdybyśmy wiedzieli, z jakiego materiału powstał ten półprzewodnik, można by było ocenić dokładność wykonywania pomiarów i obliczeń. Najbliższy temu wynikowi półprzewodnik to arsenek indu (InAs) o przerwie energetycznej równej 0,36 eV.
Wyszukiwarka