Łukasz Grzeczkowicz

IwT

Gr Aa gr II

Pomiar rezystancji metodą mostkową

Teoria:

Jeżeli pomiędzy końcami przewodnika wytworzymy różnicę potencjałów (przyłożymy napięcie), to w przewodniku powstanie pole elektryczne wywołu­jące uporządkowany ruch ładunków elektrycznych. Taki uporządkowany ruch ładunków elektrycznych nazywamy prądem elektrycznym. Przepływ prądu opi­sują prawa: Ohma i Kirchhoffa.

Zgodnie z prawem Ohma, natężenie prądu płynącego przez przewodnik jest wprost proporcjonalne do wielkości przyłożonego napięcia

Współczynnik proporcjonalności R nazywamy oporem elektrycznym przewod­nika. Jednostką oporu jest om [Ω], l om jest równy oporowi takiego przewod­nika, w którym pod napięciem 1V płynie prąd o natężeniu 1A. Wartość oporu zależy od materiału z jakiego wykonany jest przewodnik, jego kształtu i rozmia­rów. Dla jednorodnego przewodnika o długości L i stałym przekroju S

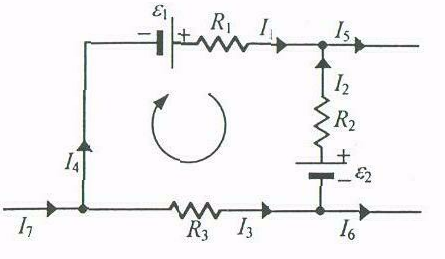
I prawo Kirchhoffa dotyczy węzłów obwodu elektrycznego. Wyraża ono zasadę zachowania ładunku elektrycznego, gdyż mówi, że suma natężeń prądów wpływających do węzła I., jest równa sumie natężeń prądów wypływających z węzła I

II prawo Kirchhoffa dotyczy obwodów zamkniętych (oczek sieci) i jest związane z zasadą zachowania energii. Stwierdza ono, że w dowolnym obwo­dzie zamkniętym (oczku) suma spadków napięć na opornikach i oporach we­wnętrznych źródeł prądu jest równa sumie sił elektromotorycznych źródeł prądu. Po uwzględnieniu prawa Ohma (2.1), II prawo Kirchhoffa można zapisać w postaci

Do pomiaru oporu metodą mostkową służy czteroramienny mostek Wheatstone'a. Ramiona mostka tworzą: badany opornik R_x, oraz trzy oporniki R₁, R₂, R₃ (w tym jeden opornik o zmiennej oporności). W przekątną mostka wbudowany jest galwanometr G. Cały układ jest zasilany ze źródła Z.

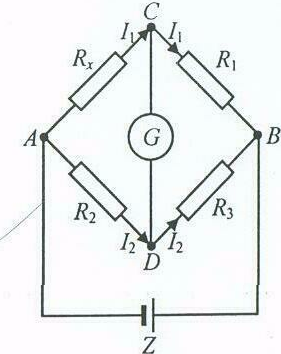
Pomiar nieznanego oporu R_x polega na zrównoważeniu mostka, tzn. takim dobraniu wartości oporu zmiennego, aby przez galwanometr nie płynął prąd (galwanometr wskazuje „0”). Ma to miejsce, gdy potencjały elektryczne punktów C i D są takie same.

Z równości tej wynika, że jeżeli w punktach A i B potencjały wynoszą odpowiednio V_A i V_B to :

Ponieważ napięcie elektryczne pomiędzy dwoma punktami jest zdefiniowane jako różnica potencjałów elektrycznych tych punktów, to napięcie pomiędzy punktami A i C jest równe napięciu pomiędzy punktami A i D oraz napięcie pomiędzy punktami C i B jest równe napięciu pomiędzy punktami D i B.

Gdy mostek jest zrównoważony, przez gałąź z galwanometrem nie płynie prąd. W takim stanie, natężenie prądów płynących przez opornik R_x i R₁ są takie same i wynoszą I₁. Podobnie, natężenia prądów płynących przez oporniki R₂ i R₃ są równe i wynoszą I₂. Na mocy prawa Ohma równania można zapisać w postaci :

Dzieląc te równania stronami i przekształcając otrzymujemy ostatecznie

Znajomość wartości R₁, R₂ i R₃ w stanie równowagi mostka pozwala więc wyznaczyć R_x.

Obliczenia :

1. Wyznaczanie rezystancji za pomocą mostka Wheatstone'a.

Korzystam z wzoru:

Obliczam wartość oporu na opornikach R₁ i R₂:

Połączyłem opory R₁ i R₂ szeregowo:

Wyliczam -

Połączyłem opory R₁ i R₂ równolegle:

Doświadczalnie -

2. Badanie relacji prądowo-napięciowych w obwodach

Zestawiam układ pomiarowy w następujący sposób :

V

mA

V

mA

Nie ma różnicy w wartościach natężenia opornika R₁ oraz opornika R₂.Natężenie jest równe sumi natężeń na poszczególnych opornikach.

1. Szeregowo

Zestawiam układ pomiarowy w następujący sposób :

V -AB

V -CD

mA

mA

V

Ma

2. Równolegle

Zestawiam układ pomiarowy w następujący sposób :

		-EF
-AB

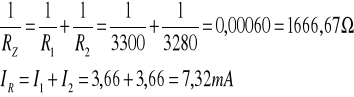
Wnioski:

W obwodzie szeregowym natężenie I₁ różni się od natężenia I₂ jednak ich suma równa się natężeniu wypadkowemu.

W obwodzie równoległym wszystkie natężenia są takie same oraz ich wypadkowe natężenie równa się każdemu poszczególnemu. Analogicznie do powyższego mają się napięcia prądu w tych przypadkach.

RACHUNEK BŁĘDU METODĄ RÓŻNICZKI ZUPEŁNEJ

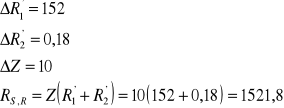
Błąd bezwzględny

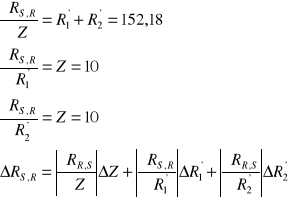
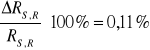
5

---