18. Możliwości zastosowania statystyki w badaniach pedagogicznych.
Statystyka jest nauką zajmującą się ilościowymi metodami badania zjawisk masowych. Zjawiska masowe to takie, które badane w dużej masie wykazują prawidłowości, jakich nie można zaobserwować w pojedynczym przypadku.
W innym rozumieniu statystyka jest zbiorem wiadomości liczbowych charakteryzujących zjawiska masowe. Mówimy np. o statystyce handlu, szkolnictwa, przemysłu itd.
Zalety metod statystycznych:
Dokładniejszy sposób opisu
Zestawienie wyników w treściwej formie
Wyciągnięcie ogólnych wniosków
Przewidywanie przebiegu zjawisk, ocena prawdopodobieństwa jakichś zdarzeń
Wyodrębnienie przyczyn niektórych zjawisk
Dzięki statystyce można dokonywać:
Grupowania danych
Budowania tabeli
Graficznej prezentacji materiału statystycznego np. wykresy, histogramy
Statystykę wykorzystujemy:
w kwestionariuszu wywiadu , najważniejszym warunkiem poprawnego przeprowadzenia wywiadu są właściwie przygotowane dyspozycje. Określa się je zazwyczaj mianem kwestionariusza. Wg Pilcha to zestaw pytań zbudowany według specjalnych zasad do przeprowadzenia wywiadu.
w kwestionariuszu ankiety, większość pytań jest zamknięta, opatrzona kafeterią (czyli zestawem wszelkich możliwych odpowiedzi ) zamkniętą lub półotwartą. Dzięki takiej konstrukcji ankieta nie wymaga dozoru ankietera, może być wysłana pocztą, wypełnia się ją szybko i łatwo. Ankieta daje wiedzę obszerną, wyliczającą, nie pogłębioną, informuje, nie wyjaśnia.
w teście socjometrycznym, najpowszechniej bada się nim strukturę, rodzaj i natężenie związków emocjonalnych zachodzących w małej grupie nieformalnej.
Socjometria jest zespołem czynności werbalnych i manipulujących mających na celu poznanie uwarunkowań, istoty i przemian nieformalnych związków międzyosobowych w grupach rówieśniczych.
Test socjometryczny nie powinien przekraczać 5 pytań w szczególności w klasach młodszych.
Organizując badania socjometryczne badający powinien uzasadnić, w jakim celu zadaje pytania. Najlepiej, jeśli posiada plan wykorzystywania wyników.
w narzędziach obserwacji , arkusz obserwacyjny to wcześniej przygotowany kwestionariusz z wytypowanymi wszystkimi zagadnieniami, które objąć ma obserwacja. W odpowiednich rubrykach, pod określonym zagadnieniem notujemy wszystkie spostrzeżenia, fakty, zdarzenia i okoliczności mające związek z danym zagadnieniem. Do narzędzi obserwacji należą: dzienniki obserwacji (codziennie przez miesiąc zapisujemy szczegółowe ustalenia płynące z obserwacji), czy też proste karty obserwacji (mogą być indywidualne lub tematyczne), oraz arkusze obserwacji (forma tabeli, podzielonej na poszczególne zagadnienia, które obserwujemy. Obserwacje są prowadzone kilka razy i nieregularnie).
w skalach, to szereg zdań ułożonych według określonego porządku, wyczerpujących możliwe określenia badanego zjawiska, cechy lub układu. Skale opisowe są zwykle używane jako część składowa innych metod badań. Jest to metoda mało skomplikowana i prosta w użyciu i z tych m.in. powodów jest szeroko stosowana.
Stopnie skali mogą być wyrażone za pomocą cyfr, przymiotników, opisów, czasowników. Liczba stopni skal ocen zależy od celu, jakiemu mają służyć badania.
Przygotowanie stopni takiej skali poprzedza zazwyczaj długotrwała i systematyczna obserwacja. Na jej podstawie sporządza się opis różnych zachowań odpowiadających różnym stopniom nasycenia cechy, którą zamierzamy się bliżej zająć.
19. Populacja a próba.
Populacja - (inaczej populacja statystyczna, populacja generalna, zbiorowość, zbiorowość generalna) - zbiór elementów, podlegających badaniu statystycznemu. Elementy populacji są do siebie podobne pod względem badanej cechy, ale nie są identyczne.
Dobór próby - wyselekcjonowanie dla celów badawczych np. pewnej liczby osób wchodzących w skład ściśle określonej zbiorowości (czyli populacji), którą badacz jest w szczególny sposób zainteresowany.
Próba może dotyczyć osób, instytucji, tekstów pisanych oraz różnego rodzaju ludzkich wytworów.
Pobieranie próby do badań z populacji opiera się na przekonaniu, że umożliwia ono wyciąganie odpowiednich wniosków o właściwościach całej populacji, bez konieczności uwzględniania w przeprowadzonych badaniach wszystkich objętych nią osób lub instytucji.
|
Osoby wyselekcjonowane do badań mają stanowić próbę reprezentatywną.
CZYLI…..
Osoby te mają być tożsame (jednakowe) pod względem zmiennych, które interesują badacza. Reprezentatywność próby odnosi się zwykle tylko do jednej lub kilku badanych cech.
Po sformułowaniu problemów badawczych i hipotez badacz musi dokonać poprawnego doboru badanych osób, z powodu zbyt dużej liczebnie populacji ale i również aby uniknąć nadmiernych nakładów czasu i pieniędzy oraz aby wyniki, o które chodzi można było uzyskać badając tylko część tej populacji.
Wdzięcznym przedmiotem badań są dzieci i młodzież o charakterystycznych dla nich cechach osobowości i zachowania.
Spośród dzieci wyodrębnia się na ogół dzieci w młodszym i starszym wieku szkolnym, które wyróżnia się np. ze względu na płeć, pochodzenie społeczne i sytuację rodzinną.
Trzy sposoby dokonywania doboru próby:
1. dobór losowy (inaczej probabilistyczny - uznawany za najlepszy) - umożliwia wnioskowanie o populacji oparte na rachunku prawdopodobieństwa, nie chodzi tutaj o dowolny typ przypadku, lecz o zastosowanie takiej metody doboru przypadkowego elementu populacji do badanej próby, aby każdy z nich miał określone szanse bycia wylosowanym do badania
rodzaje doboru losowego:
prosty dobór próby- wyciąganie odpowiednio ponumerowanych kartek z pojemnika dokładnie wcześniej wymieszanych lub kart z leżącej odpowiednio potasowanej talii kart (techniki z gier losowych jak np. totolotek)
systematyczny dobór próby - np. wywołanie co piątego ucznia w klasie do odpowiedzi zgodnie z zapisem w dzienniku lekcyjnym
warstwowy dobór próby - stosowany zazwyczaj w bardzo zróżnicowanej populacji, polega na wyłowieniu z niej podgrup zwanych warstwami, jest to np. podział (rozwarstwienie) uczniów ze względu na płeć, wiek, miejsce zamieszkania, pochodzenie społeczne, poziom osiągnięć szkolnych, sytuację rodzinną
grupowy dobór próby - dokonuje się grupowego doboru próby np. kilku zaledwie klas spośród wszystkich klas całej szkoły
wielostopniowy dobór próby - jest odmianą grupowego doboru próby (wielostopniowy, zwłaszcza dwustopniowy) zazwyczaj polega na wylosowaniu najpierw np. jakiejś jednej szkoły, a następnie klas, które zamierza się poddać badaniom
2. dobór celowy - o tym kto zostanie zakwalifikowany do badanych osób z danej grupy, decyduje sam badacz. Kieruje się przy tym posiadaną wiedzą o interesującej go populacji, pod względem charakteryzujących ją cech. Wiedza ta ma być dokładna, ponieważ wartość poznawcza zgromadzonych danych będzie zależeć w dużym stopniu od bardziej lub mniej trafnego celowego doboru badanych osób. Celowy dobór próby raczej rzadko kiedy jest w stanie zapewnić jej wystarczającą reprezentatywność. Wyjątek stanowią badania jakościowe, w których z reguły pobiera się próbę w sposób celowy. Czyni się to zawsze po dokładnym rozpoznaniu osób zakwalifikowanych do badania. Badacz jest zazwyczaj osobą obcą czy anonimową dla osób wybieranych.
rodzaje doboru celowego:
kwotowy dobór próby - są to odpowiednie kwoty (ilości) osób o różnorodnych rozkładach cech, które należy uwzględnić w planowanych badaniach. Wykorzystuje się je często w badaniach dotyczących opinii badanych osób w różnych sprawach, szczególnie przy sondażu opinii publicznej. Od badacza zależy kogo poprosi o odpowiedzi na pytania ankietowe. Prawdopodobniej najchętniej wybierze osoby do których ma łatwy dostęp, dlatego też dobrana przez niego próba może być obciążona. Aby dobrać odpowiednio próbę trzeba mieć odpowiednią wiedzę na temat całej populacji. Poza tym nigdy nie ma pewności czy osoby które odmówiły odpowiedzi były by bardziej reprezentatywne niż osoby które udało się namówić na udział w ankiecie.
3.dobór na podstawie ochotniczych zgłoszeń - całkowicie dobrowolne zgłaszanie się do badań osób, do których badacz zwraca się najczęściej w formie pisemnej. Są to przeważnie badania ankietowe. Nie wszyscy zdają sobie sprawę z pozornej trafności tego rodzaju próby. Bywa zazwyczaj niewiarygodna. Badacz prawdopodobnie nigdy nie dowie się jakimi motywami kierowały się osoby, które deklarowały swój udział w badaniach i jakie cechy osobowości różnią ich od osób które odmówiły udziału w ankiecie. Wyniki mogą również być nietypowe w stosunku do całej populacji. Lecz potrzebę doboru próby w taki właśnie sposób uzasadniają niektóre cele badań dotyczące np. intymnej sfery życia dzieci, młodzieży i dorosłych, molestowania seksualnego, sprawy związane ze światopoglądem, system wartości, sens życia.
Mimo to i w tym wypadku ochotniczy dobór próby zostawia pewne wątpliwości. Dlatego pierwszeństwo w badaniach daje się losowemu i celowemu doborowi próby.
20. Parametry i estymatory.
Parametr jest to właściwość opisująca populację, a estymator jest to właściwość próby pobranej losowo populacji. Zakłada się, że wartość uzyskana przy badaniu próby jest estymatorem odpowiedniego parametru populacji. Zazwyczaj parametry, (czyli wartości populacji) pozostają nieznane.
Wielu autorów przyjmuje, że parametry oznacza się literami greckimi, estymatory zaś łacińskimi (np. symbol σ i symbol s jako odchylenie standardowe)
Mierzymy jedynie estymatory!
23. Zmienne, wskaźniki, skale pomiarowe - pojęcie i klasyfikacja.
Zmienne
Cechy, właściwości, mają różne wartości( pod względem których elementy zbioru się miedzy sobą różnią) może przyjmować co najmniej 2 wartości (płeć, wiek, kolor oczu, inteligencja, otyłość słuchu)
Możemy określać za pomocą liczb lub nazw:
*płeć, kraj, pochodzenie, zawód, religia wartości takiej zmiennej wyrażamy nazwami
*wzrost, waga, inteligencjawartości takiej zmiennej wyrażamy liczbowo
ZAWÓDzmienna
LEKARZwartość zmiennej
WYZNANIEzmienna
KATOLIKwartość zmiennej
KOLOR OCZUzmienna
ZIELONEwartość zmiennej
Podział Zmiennych
Zależne i Niezależne
Ciągłe
To takie, które mogą przyjmować dowolne wartości z danego zakresu
*wzrost między 170 a 190 można wstawić różne (nieskończone wartości)
-ciężar
-czas
-temperatura
Nieciągła (dyskretna)
Może przyjmować tylko niektóre wartościzazwyczaj całkowite
*liczba dzieci1,2,3…
*liczba osób w rodzinie1,2,3…
Zmienne i ich klasyfikacja
Nominalna
Porządkowa(rangowa)
Przedziałowa
Stosunkowa
1.Nominalna
taka właściwość, która jest wyznaczona przez operację, jej mierzenie polega na stwierdzeniu, że coś jest takie samo, lub różne
w przypadku tej zmiennej można stwierdzić, że jeden element jest po względem interesującej nas właściwości jest taki sam lub inny niż drugi element
OPISUJEMY NAZWAMI
zawód, płeć, kolor oczu
RównośćRóżność
Taki sam kolor oczuróżny
Katoliknie katolik
2.Porządkowa
wiąże się z porządkowaniem, z operacją szeregowania
*można stwierdzić
„większy niż” i „mniejszy niż”
„równy” i „różny”
przykład
Uszeregowanie osób według stopnia agresywności, pracowitości
*Dopuszczalnymi statystykami i testami istotności są:
Mediana, centyle, decyle, kwadryle, wpółczynnik korelacji R Spearmana
CENTYLE -takie wartości pomiaru zmiennej, poniżej których znajduje się określany procent(odsetek) wszystkich wyników(pomiarów)
Np. 20 centyl to będzie taki wynik poniżej którego jest 20% wszystkich pomiarów
DECYLE-dziesiątki centyli
KWADRYLE- dwudziestki piątki centyli (ćwiartki)
3.Przedziałowa
-jest właściwościa, którą określamy przez operację oprócz wcześniejszych twierdzeń, (o różności przedziałów)
„o ile większy”, „o ile mniejszy”
„większy niż”, „mniejszy niż”
„równy”, „różny”
czas i temperatura
umownie można określić punkt zerowy
Np. temperatura(np.. skali Celsjusza, jak również czas kalendarzowy)
*Dopuszczalne statystyki
wszystkie wcześniejsze plus średnia arytmetyczna, wariancja, odchylenie standardowe, wpółczynnik korelacji R Pearsona, test T->student
4.Stosunkowa
”ile razy coś jest mniejsze większe”również wcześniejsze stwierdzenia
jest tu zawsze taka wartość poniżej zmiennej w ogóle nie ma jest ZERO ABSOLUTNE
liczby które będą wskazane będą odzwierciedlały odległość od naturalnego początku
*przykładydługość, ciężar, liczebność zbioru
--nie można powiedzieć że ktoś ma -3 cm wzrostu
Na wynikach tej zmiennej można wykonywać wszelkie działania arytmetyczne
2.Tak samo dzielą się skale!
3.Wskaźniki
Są nimi mierzalne cechy czy właściwości badanych faktów, czy zjawisk lub czynniki mające na nie wpływ albo skutki, jakie pociągają one za sobą.
Zgodnie z sugestią S. Nowaka „wskaźnikiem jakiegoś zjawiska Z nazywać będziemy takie zjawisko W, którego zaobserwowanie pozwoli nam (w sposób bezwyjątkowy lub z określonym czy choćby wyższym od przeciętnego prawdopodobieństwem) określić, iż zaszło zjawisko Z”
Podział wskaźników
Empiryczne
Występują wtedy, gdyż wskazywane przez nie zjawisko daje się łatwo i bezpośrednio zaobserwować. Stąd też zachodząca relacja między nimi a danym zjawiskiem ma charakter związku empirycznego. To znaczy o powiązaniu danego wskaźnika (lub wskaźników ze zjawiskiem wskazanym możemy się przekonać niejako „naocznie” za pomocą bezpośredniej obserwacji.
Tak np. na podstawie ubioru ucznia możemy wnioskować o stanie
Zamożności jego rodziny albo w oparciu o ład i porządek w klasie podczas lekcji o zdyscyplinowaniu jej uczniów.
Wskaźniki empiryczne w postaci pytań o opinie pozwalają na wyeliminowanie pytań zbędnych i uwzględnienie tylko tych najważniejszych. Przede wszystkim zaś muszą się one liczyć z możliwością odpowiadania na nie ze strony osób badanych.
Definicyjne
Mają miejsce wówczas, gdy wynikają z definicji badanego zjawiska lub faktu. „W takim przypadku nadajemy sens danemu terminowi za pomocą badania jego pełnej bądź cząstkowej definicji, w której wskaźnik jest członem definiującym”.
Np. wskaźnikiem pozycji społecznej, jaką zajmuje uczeń w klasie szkolnej jest liczba uzyskanych przez niego wyborów podczas badań socjometrycznych.
Wśród wskaźników definicyjnych wyróżnia się na ogół dwie ich kategorie
Do pierwszej z nich zalicza się te, które „definiują nam pewne zespoły zjawisk, zdarzeń czy zachowań bezpośrednio obserwowalnych”
Do drugiej natomiast zalicza się takie wskaźniki, które definiują nam dyspozycje do takich zachowań czy występowanie odpowiednich zdarzeń, jeśli dyspozycja znaczy jedynie tyle, co częste pojawianie się czy też pojawianie się w określonych okolicznościach określonej właściwości i zachowania”
Pierwsza kategoria wskaźników definicyjnych odnosi się do pewnych aktualnych cech jednostek ludzkich lub ich grup druga wyraża pewne potencjalne możliwości tych jednostek lub grup , aktualizowane w ściśle określonych sytuacjach i jednostkach
Inferencyjne
Odnoszą się do zjawisk bezpośrednio nieobserwowalnych i nie wchodzą do definicji badanych zjawisk. Wskaźniki inferencyjne dotyczą ukrytych hipotetycznych zmiennych, które wprawdzie są nieobserwowalne, ale posiadają osobliwą „realność i szereg obserwowalnych następstw”.
22. Rozkłady liczebności i zasady ich sporządzania.
Dane z badań są często zbiorami liczb. Dla ich zrozumienia i interpretacji potrzebne są pewne formy klasyfikacji i opisu. Najprostszą odmianą klasyfikacji danych jest rozkład liczebności.
ROZKŁAD LICZEBNOŚCI - każde uporządkowanie danych, które pokazuje liczebność różnych wartości zmiennej lub liczebności wartości należących do dowolnie określonych grup zmiennej, zwanych przedziałami klasowymi.
Przykład 1:
Rzucamy 10 razy monetą i otrzymujemy następujące wyniki:
OOROROOORO
Liczba wyrażająca ile razy pojawił się orzeł (liczebność orła) - 7
Liczba wyrażająca ile razy pojawiła się reszka (liczebność reszki) - 3
Przykład 2:
Rzucamy kostka do gry 24 razy i otrzymujemy następujące wyniki:
6,3,1,4,1,6,5,2,4,3,5,5,4,1,5,2,2,6,5,3,3,4,5,5;
Liczby pojawiające się przy rzucaniu kostką tworzą zmienną X, która przybiera wartości 1,2,3,4,5,6;
W powyższych danych:
6 pojawia się 3 razy
5 pojawia się 7 razy
itd.
Rozkłady liczebności inaczej nazywamy szeregami statycznymi
SZEREG STATYSTYCZNY - to odpowiednie pogrupowanie zbiorowości statystycznej i jej uporządkowanie (od najniższej do najwyższej wartości jakiejś cechy lub odwrotnie).
Szereg przeważnie składa się z 2 kolumn (rzadziej wierszy), z których jedna podaje wartość cechy w poszczególnych pozycjach, a druga podaje ilość jednostek przypadających na daną wartość cechy.
PRZEDZIAŁ KLASOWY - dowolnie określone grupy wartości zmiennych.
W uporządkowaniu danych przy przedziale klasowym równym 1 (jak w tabeli 2.2) zachowane zostają oryginalne wyniki i można je odtworzyć bezpośrednio z rozkładu liczebności bez żadnej straty informacji. Jeżeli przedział klasowy jest większy (3, 5 lub 10) to narażamy się na stratę informacji dotyczących pojedynczych wyników. Na podstawie rozkładu liczebności nie można dokładnie odtworzyć wyników oryginalnych.
Przedział nie może być ani za mały, ani za duży.
Reguły doboru przedziałów klasowych:
Przedział klasowy powinien mieć taki rozmiar by 10 do 20 przedziałów objęło wszystkie wyniki.
Przedziały klasowe powinny być równe 1,3,5,10 lub 20 punktów - za ich pomocą da się uporządkować większość zbiorów danych.
Zaczynać przedział klasowy od wartości, która stanowi wielokrotność rozmiaru tego przedziału np. przy przedziale klasowym równym 5 przedział powinien zaczynać się od wartości 5,10,15,20 itd.
Uporządkować przedziały klasowe według wielkości wyników, które zawierają, najwyżej umieszczając przedział zawierający najwyższe wyniki.
Granice dokładne przedziałów klasowych:
Jeżeli mamy do czynienia ze zmienną ciągłą, a nie dyskretną, wybieramy jakąś jednostkę pomiarową i zapisujemy wyniki w postaci wartości dyskretnych. Przyjmujemy, że wartość zapisana przedstawia wartość rzeczywistą mieszcząc się w pewnych granicach. Granice umieszczone są zazwyczaj w połowie jednostki pomiarowej poniżej i powyżej wartości zapisanej.
Pojęciem granic dokładnych przedziału klasowego posługujemy się w przypadku zmiennej ciągłej. W przypadku wartości dyskretnych nie trzeba przeprowadzać rozróżnienia między przedziałem klasowym a granicami dokładnymi przedziału, ponieważ są one tożsame.
Grupowanie danych w przedziale klasowym powoduje utratę informacji dotyczących pojedynczych wyników. Wyniki mogą bowiem różnić się między sobą w pewnym zakresie, a mimo to są zapisywane w tym samym przedziale.
Przy obliczaniu niektórych statystyk oraz graficznym przedstawieniu wyników niezbędne jest poczynienie pewnych założeń dotyczących wartości w obrębie przedziałów:
Wyniki w przedziale rozkładają się równomiernie w dokładnych granicach przedziału. Założenie to przyjmuje się przy obliczaniu takich statystyk jak: mediana, kwartyle, centyle oraz przy rysowaniu histogramów.
Centyl - taka wartość na skali pomiarowej, poniżej której znajduje się określony procent wszystkich naszych pomiarów np. 20 centyli to jest wartość na naszej skali pomiarowej, poniżej której znajduje się 20 wyników lub pomiarów.
Kwartyle od kwarta - ćwierć, to są 25 centyli
1 kwartyl - 25 centyli
2 kwartyle - 50 centyli
3 kwartyle - 75 centyli
Wszystkie wyniki skupiają się w środku przedziału, czyli są takie same - równe wartości odpowiadającej środkowi przedziału. Środek dowolnego przedziału klasowego leży w połowie między dokładnymi granicami tego przedziału. Założenie to przyjmuje się zazwyczaj przy obliczaniu takich statystyk jak średnia, odchylenie standardowe przy rysowaniu krzywych liczebności.
Rozkłady liczebności skumulowanych:
Czasami interesują nas nie liczebności w obrębie samych przedziałów klasowych, lecz procentowy udział wartości „większych niż” bądź „mniejszych niż” pewna określona wartość. Informację uzyskamy sporządzając rozkład liczebności skumulowanych.
Liczebności skumulowane otrzymujemy dodając, począwszy od dołu, liczebności jednostkowe.
Rozkład liczebności skumulowanych pozwala stwierdzić, w jakiej liczbie przypadków wyniki są niższe od pewnej określonej wartości.
Skumulowane procenty liczebności (otrzymuje się przez podzielenie liczebności skumulowanej przez całkowitą liczbę przypadków) pokazują procent jednostek, które uzyskały wynik niższy od pewnej wartości.
Zapis statystyczny
Zastosowanie symboli i reguł posługiwania się nimi zwiększa możliwości przedstawiania oraz analizowania danych. Najczęściej stosowaną postacią zapisu statystycznego jest zapis sumowania, który opiera się na kilku prostych zasadach
Zbiór wartości, pomiarów lub wyników można zapisać w postaci: X1, X2, X3, .... , XN albo Y1, Y2, Y3, .... , YN, gdzie N oznacza liczbę wartości zmiennej, a symbole X i Y oznaczają zmienne
Liczby 1,2,3, ... , N określa się mianem indeksów. Pozwalają one na zidentyfikowanie konkretnego elementu.
Jeżeli przy N=5 wyniki wynoszą: 95, 102, 105, 113, 127 to X1= 95, X2= 102, X3=105 itd.
Dowolną wartość zmiennej przyjęło się określać symbolem Xi , gdzie indeks i może przyjmować dowolną wartość od 1 do N. Jako indeksów używa się również symboli j oraz k.
Sumowanie wartości zmiennej
Sumę przedstawia się następująco:
N
Σ Xi
i=1
A zatem:
N
Σ Xi = X1 + X2 + .... + XN
i=1
Symbol Σ, - grecka litera sigma, określa prostą operację dodawania elementów. To znak sumowania.
Symbole znajdujące się nad i pod tym znakiem określają granice sumowania. Zatem wcześniejszy zapis oznacza dodawanie do siebie wszystkich wartości zmiennej, gdzie
i przyjmuje wartości od i=1 do i=N.
Wyrażenie typu 5
Σ Xi oznacza sumę pierwszych pięciu wartości zmiennej Xi, i=1 czyli od i=1 do i=5
23. Przeciętne i miary dyspersji.
Miary dyspersji
Wariancja
a/ szereg szczegółowy - wariancja nieważona
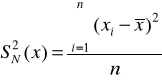
b/ szereg rozdzielczy- wariancja ważona
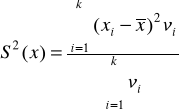
Odchylenie standardowe (miara absolutna)
![]()
Interpretacja: przeciętne odchylenie wartości cechy od średniej arytmetycznej
Typowy obszar zmienności:
x-S(x) < xtyp < x+ S(x)
Klasyczny współczynnik zmienności (miara stosunkowa)
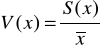
Ocena siły dyspersji (skala trójstopniowa):
0,0-0,30 słaba dyspersja
0,31-0,60 umiarkowana
powyżej 0,60 silna
MIARY PRZECIĘTNE
Miary przeciętne charakteryzują średni lub typowy poziom wartości cechy, wokół których skupiają się wszystkie pozostałe wartości analizowanej cechy |
średnia arytmetyczna średnia harmoniczna średnia geometryczna modalna |
MIARY PRZECIĘTNE KLASYCZNE
♦średnia arytmetyczna
Średnią arytmetyczną - definiuje się jako sumę wartości cechy mierzalnej podzieloną przez liczbę jednostek skończonej zbiorowości statystycznej.
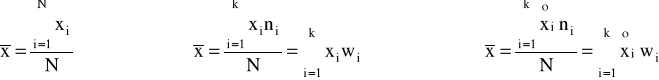
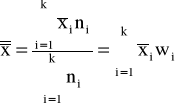
Wybrane właściwości średniej arytmetycznej
suma wartości cechy jest równa iloczynowi średniej arytmetycznej i liczebności zbiorowości:
lub dla szeregu rozdzielczego
,średnia arytmetyczna spełnia warunek:
,suma odchyleń poszczególnych wartości cechy od średniej równa się zero:
lub
,Suma kwadratów odchyleń poszczególnych wartości cechy od średniej jest minimalna:
lub
,średnią arytmetyczną można liczyć w zasadzie dla szeregów o zamkniętych przedziałach klasowych; jeżeli liczebność w otwartym przedziale klasowym stanowi niewielki odsetek, (praktycznie do 5%) możliwe jest domknięcie przedziałów klasowych oraz obliczenie średniej w innym przypadku do określenia zjawiska stosuje się parametry pozycyjne,
średnia arytmetyczna jest wrażliwa na skrajne wartości cechy,
średnia arytmetyczna z próby jest dobrym przybliżeniem wartości przeciętnej.
♦średnia harmoniczna
Średnią harmoniczną - stosuje się wtedy, gdy wartości cechy są podane w przeliczeniu na stałą jednostkę innej zmiennej, czyli w postaci wskaźników natężenia, wagi natomiast w jednostkach liczników tych cech, np. prędkość pojazdu w km/h.
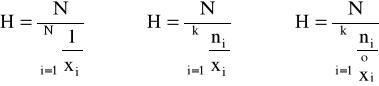
♦średnia geometryczna
Średnią geometryczną - stosuje się w badaniach średniego tempa zmian zjawisk, a więc gdy zjawiska są ujmowane dynamicznie.
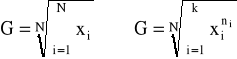
MIARY PRZECIĘTNE POZYCYJNE
♦dominanta (moda)
1) dla przedziałów o równej rozpiętości
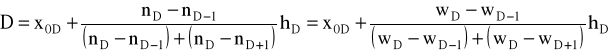
2) dla przedziałów o nierównej rozpiętości
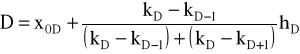
, gdzie 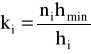
natężenie liczebności
♦kwartyle
kwartyl pierwszy
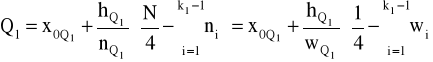
mediana (kwartyl drugi)
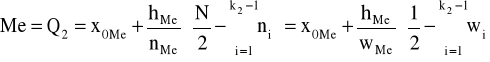
kwartyl trzeci
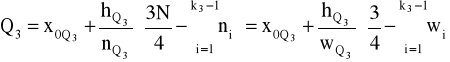
Odchylenie ćwiartkowe (miara absolutna)
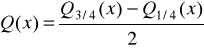
Interpretacja: średnia rozpiętość cechy w dwóch środkowych ćwiartkach rozkładu.
24. Regresja i korelacja
Regresja to w statystyce metoda, pozwalająca na zbadanie związku pomiędzy różnymi wielkościami występującymi w danych i wykorzystanie tej wiedzy do przewidywania nieznanych wartości jednych wielkości na podstawie znanych wartości innych.
Użycie regresji w praktyce sprowadza się do dwóch faz:
konstruowanie modelu - budowa tzw. modelu regresyjnego, czyli funkcji, opisującej jak zależy wartość oczekiwana zmiennej objaśnianej od zmiennych objaśniających. Funkcja ta może być zadana nie tylko czystym wzorem matematycznym, ale także całym algorytmem, np. w postaci drzewa regresyjnego, sieci neuronowej, itp.. Model konstruuje się tak, aby jak najlepiej pasował do danych z próby, zawierającej zarówno zmienne objaśniające, jak i objaśniane (tzw. zbiór uczący). Mówiąc o wyliczaniu regresji ma się na myśli tę fazę.
stosowanie modelu (scoring) - użycie wyliczonego modelu do danych w których znamy tylko zmienne objaśniające, w celu wyznaczenia wartości oczekiwanej zmiennej objaśnianej.
Korelacja odnosi się do współzależności zjawisk (np.czy jest związek pomiędzy wynikami testu na inteligencję a sukcesami w pracy zawodowej).
Współczynnik korelacji to liczba, która mówi, w jakim stopniu zjawiska są powiązane, w jakim stopniu zmianie jednego zjawiska odpowiada zmiana drugiego. Dzięki temu możliwe jest przewidywanie.
Między zmiennymi mogą zachodzić następujące stosunki korelacyjne:
1. zgodności (korelacja dodatnia)
2. przeciwieństwa (korelacja negatywna, ujemna)
3. niezależności (brak korelacji)
Standardowym współczynnikiem korelacji, najczęściej obliczanym, jest współczynnik według momentu iloczynowego Pearsona.
rxy - korelacja między zmiennymi X i Y
x - odchylenia poszczególnych wyników pomiaru zmiennej X od średniej pomiarów
y - odchylenia poszczególnych wyników pomiaru zmiennej Y od średniej pomiarów
σx oraz σx - odchylenia standardowe rozkładu wyników X i Y
TABELA 2
Współczynnik korelacji Pearsona z danych nie pogrupowanych według momentu iloczynowego
Badany |
X |
Y |
x |
y |
x2 |
y2 |
x y |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
1 |
24 |
82 |
0 |
+12 |
0 |
144 |
0 |
Sumy |
360 |
1050 |
0 |
0 |
454 |
454 |
+933 |
Przykład: Obliczenie współczynnika rxy pokazano w tabeli 2.
Współczynnik rxy przyjmuje wartości z przedziału od +1 (całkowita korelacja dodatnia), poprzez 0 (brak jakiejkolwiek korelacji) aż do -1 (całkowita korelacja ujemna).
Interpretacja współczynnika korelacji:
1. poniżej 0,20: korelacja słaba (zależność prawie nic nie znacząca)
2. 0,20-0,40: korelacja niska (zależność wyraźna, lecz mała)
3. 0,40-0,70: korelacja umiarkowana (zależność istotna)
4. 0,70-0,90: korelacja wysoka (zależność znacząca)
5. 0,90-1,00: korelacja b. wysoka (zależność bardzo pewna)
25. Zastosowanie testów t Studenta i x2
Test t Studenta przeważnie służy do określania istotności różnic pomiędzy otrzymanymi wynikami pomiaru badanej cechy (np. pomiędzy średnimi ocenami w grupie eksperymentalnej i kontrolnej).
Student to pseudonim W. S. Grosseta.
Statystyka t Studenta jest stosunkiem odchylenia od średniej (lub innego parametru) w rozkładzie statystyk z prób do błędu standardowego tego rozkładu.
Powinny być spełnione 2 warunki:
Zmienna ma rozkład normalny;
Próba jest mała, tzn. N<30 (wg innych N<100).
Statystyką t Studenta można posłużyć się do wyznaczenia istotności różnic pomiędzy:
średnimi nieskorelowanymi (por. tabele 3a i 3b);
TABELA 3a
Chłopcy (X1) |
Dziewczęta (X2) |
52 |
50 |
X1=387 |
X2=390 |
Dla sprawdzenia istotności powyższych różnic między nieskorelowanymi średnimi zastosujemy test t, na obliczenie którego wzór jest następujący:
gdzie:
M1 i M2 - odpowiednio średnie arytmetyczne próby pierwszej i próby drugiej,
N1 i N2 - odpowiednio liczebności próby pierwszej i próby drugiej,
Sx12 i S x22 - odpowiednio sumy kwadratów odchyleń od średniej w próbie pierwszej i w próbie drugiej.
TABELA 3b
X1 |
x1=X1-M1 |
x12 |
X2 |
x2=X2-M2 |
x22 |
1 |
2 |
3 |
4 |
5 |
6 |
52 |
+9 |
81 |
50 |
+11 |
121 |
x12 = 312 |
x22 = 326 |
||||
średnimi skorelowanymi (por. tabela 4).
TABELA 4
Obliczenia do wyznaczania współczynnika t Studenta dla ustalenia istotności różnicy między średnimi skorelowanymi
Badani |
X1 |
X2 |
Różnica |
Odchylenia od średniej różnic |
Kwadrat odchyleń |
1 |
2* |
3* |
4 |
5 |
6 |
1 |
113 |
107 |
+6 |
+4 |
16 |
|
2300 |
2260 |
+40 |
xd = 0,0 |
xd2 = 2064 |
gdzie:
Md - średnia różnic N par obserwacji,
Sxd2 - kwadrat odchyleń różnicy od średniej różnic.
Liczba stopni swobody, jaką należy stosować tutaj do obliczenia t wynosi N-1, przy czym N oznacza liczbę par obserwacji. Dane liczbowe z powyższego przykładu są następujące: Md = 2,0, Sxd2 = 2064, df = 20-1=19. Po podstawieniu:
Wzory dla średnich nieskorelowanych (drugi wzór pod tabelą 4):
Oznaczenia:
M1 i M2 - odpowiednie średnie arytmetyczne próby pierwszej i drugiej;
N1 i N2 - liczebności próby pierwszej i drugiej;
Σx12 i Σx22 - odpowiednio sumy kwadratów odchyleń od średniej w próbie 1-ej i 2-ej.
Dla przykładu z tabel 3a i b obliczone t wynosi 1,42.
Z tabeli III (w „Dodatku”) odczytujemy wartość krytyczną (istotną na poziomie ufności 0,01) dla t przy (N1+N2-2) stopniach swobody. Wynosi ona:
t0,01df=17=2,898
Interpretacja: obliczona wartość t=1,42 jest mniejsza od wartości krytycznej na poziomie 0,01 wynoszącej ~2,90, a zatem mieści się w obszarze krytycznym przyjęcia hipotezy zerowej (głoszącej, że nie ma istotnych różnic między tymi średnimi). Nie możemy odrzucić H0, bo różnica między średnimi wynikami chłopców i dziewcząt nie jest istotna na poziomie 0,01.
Wzór dla średnich skorelowanych:
Oznaczenia:
Md - średnia różnic N par obserwacji;
N - liczba par obserwacji;
Σxd2 - suma kwadratów odchyleń poszczególnych różnic od średniej różnic.
Dla przykładu z tabeli 4 obliczone t wynosi 0,86.
Z tabeli III (w „Dodatku”) odczytujemy wartość krytyczną (istotną na poziomie ufności 0,01) dla t przy (N-1) stopniach swobody. Wynosi ona:
t0,01df=19=2,86; t0,05df=19=2,09
Interpretacja: obliczona wartość t=0,86 mieści się w obszarze przyjęcia hipotezy zerowej na obu poziomach ufności. Nie możemy odrzucić H0, czyli średnie wyniki pomiaru grupy 20 osób dwoma testami nie różnią się między sobą w stopniu istotnym.
Chi-kwadrat (X2).
Chi-kwadrat to test mający różnorakie zastosowania.
Chi-kwadrat jest to suma kwadratów stosunków rozbieżności między liczebnością zaobserwowaną a liczebnością oczekiwaną na podstawie hipotezy, którą weryfikujemy.
Ogólny wzór na chi-kwadrat:
fo - liczebność zaobserwowana;
fe - liczebność oczekiwana.
Najczęściej X2 obliczamy z danych przedstawionych w tzw. tabelach wielodzielczych.
TABELA 5
C2 z tablicy wielodzielczej (aktywność społ. uczniów)
|
zorganizow. |
niezorganizow. |
RAZEM |
bierni społecznie |
fo 45 |
fo 37 |
fw 82 |
aktywni społecznie |
fo 73 |
fo 49 |
fw 122 |
SUMA |
S fk 118 |
fk 86 |
N 204 |
liczebności zaobserwowane
|
zorganizow. |
niezorganizow. |
RAZEM |
bierni społecznie |
fe 47,4 |
fe 34,6 |
82,0 |
aktywni społecznie |
fe 70,6 |
fe 51,4 |
122,0 |
SUMA |
118,0 |
86,0 |
204,0 |
spodziewane liczebności aktywnych i biernych społecznie w grupach uczniów
zorganizowanych i niezorganiz.
|
fo |
fe |
fo-fe |
(fo-fe)2 |
(fo-fe)2 |
aktywni zorg. |
73 |
70,6 |
+2,4 |
5,76 |
0,08 |
aktywni niezorg. |
49 |
51,4 |
-2,4 |
5,76 |
0,11 |
bierni zorg. |
45 |
47,4 |
-2,4 |
5,76 |
0,12 |
bierni niezorg. |
37 |
34,6 |
+2,4 |
5,76 |
0,17 |
obliczenia dla C2
C2 = 0,48
0,48 < 3,841 oraz 0,48 < 6,635 X2 jest statystyką nieparametryczną (jest niezależna od rozkładu zmiennej).
W tym przypadku rozkład zmiennej nie musi być normalny, a liczebność pomiarów może być dowolna.
Σfw - suma liczebności zaobserwowanych w wierszu;
Σfk - suma liczebności zaobserwowanych w kolumnie;
N - liczebność ogólna.
...jemy następujące liczebności ...kiwane (fe):
...organizowani:
...=70,6;
...ganizowani:
...1,4;
...wani: (82·118):204=47,4;
...zowani: (82·86):204=34,6
Budujemy tabelę oczekiwanych liczebności uczniów aktywnych i biernych społecznie wśród uczniów zorganizowanych i niezorganizowanych (tabela środkowa).
Następnie obliczamy X2 (tak jak pokazano w ostatniej tabeli).
X2=0,48
Obliczamy liczbę stopni swobody - df
df=(w-1)·(k-1), gdzie:
w - liczba wierszy w tabeli;
k - liczba kolumn w tabeli.
Zatem nasze df = (2-1)·(2-1)=1
Z tabeli V (w „Dodatku”) otrzymujemy:
X20,05df=1=3,841; X20,01df=1=6,635
Nasze X2=0,48 jest mniejsze od wartości odczytanych z tabeli V na obu poziomach ufności, zatem H0 należy przyjąć. To oznacza brak istotnej różnicy między aktywnością społeczną uczniów zorganizowanych i niezorganizowanych.
1
Wyszukiwarka