Zagadnienia aproksymacji jednostajnej i aproksymacji średniokwadratowej są również formułowane dla funkcji określonych na dyskretnym zbiorze argumentów. Dla takich funkcji warunek (5.61) dotyczący aproksymacji jednostajnej zmienia się w ten sposób, że zamiast ciągłej zmiennej niezależnej x występuje w nim zmienna dyskretna
![]()
(5.63)
a w warunku (5.62) na minimum odchylenia kwadratowego całka jest zastępowana sumą
![]()
(5.64)
Aproksymacja średniokwadratowa funkcji określonych na dyskretnym zbiorze argumentów jest najczęściej wykorzystywana w zastosowaniach praktycznych do wygładzania danych eksperymentalnych i wyników obliczeń ze względu na mniej skomplikowane algorytmy jej realizacji numerycznej w porównaniu z algorytmami aproksymacji jednostajnej i możliwość uzyskiwania dobrych przybliżeń funkcji W niektórych przypadkach istnieją przesłanki teoretyczne co do doboru postaci wzoru dla funkcji aproksymującej (wskazując dostatecznie wąską klasę funkcji np. zbiór funkcji liniowych, potęgowych, wykładniczych itp.) - wtedy określamy tylko wartości liczbowe parametrów, przy których przybliżenie danej funkcji jest najlepsze.
5.4. Aproksymacja średniokwadratowa wielomianami
W zadaniach aproksymacji średniokwadratowej wielomianami funkcji aproksymującej wygodnie jest poszukiwać - podobnie jak w zadaniu interpolacji - w postaci wielomianu uogólnionego
![]()
(5.65)
będącego kombinacją liniową liniowo-niezależnych funkcji (4.6).
Rozważymy najpierw aproksymację średniokwadratową funkcji ![]()
określonej na dyskretnym zbiorze argumentów. W tym przypadku współczynniki ( j = 0, 1, ..., m) funkcji (5.65) dobieramy tak, żeby funkcja
![]()
(5.66)
osiągnęła wartość minimalną.
Zgodnie z ogólnymi metodami rachunku różniczkowego funkcja osiąga minimum wtedy i tylko wtedy, gdy znikają pochodne cząstkowe względem wszystkich zmiennych
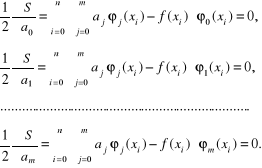
Stąd otrzymujemy układ równań z niewiadomymi współczynnikami , zwany układem normalnym:

(5.67)
w którym wprowadzono skrócone oznaczenie
![]()
(5.68)
Układ równań (5.67) ma dokładnie jedno rozwiązanie dla liniowo-niezależnego układu funkcji: ..., Macierz współczynników układu (5.67) jest macierzą symetryczną i dodatnio określoną.
Dla układu funkcji bazowych tworzących ciąg wielomianów ( j = 0, 1, ..., m) układ równań (5.67) przyjmie postać:
(5.69)
gdzie:
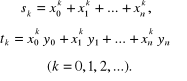
(5.70)
Wielomian aproksymujący daną funkcję ![]()
w sensie najmniejszych kwadratów
![]()
(5.71)
powinien mieć stopień na tyle wysoki, aby dostatecznie przybliżał funkcję ![]()
, a jednocześnie mieć stopień wystarczająco niski, aby wielomian ten wygładzał błędy losowe wynikające np. z pomiarów. Jeśli m = n, to wielomian aproksymujący pokrywa się z wielomianem Lagrange'a dla układu punktów: i wtedy S = 0. Wiadomo, że dla m ≥ 6 układ (5.69) jest układem źle uwarunkowanym, wskutek czego otrzymane wyniki mogą być bardzo zaburzone i nie nadawać się do praktycznego wykorzystania [1]. Podobnie więc jak w przypadku interpolacji aproksymację średniokwadratową wielomianami potęgowymi (5.71) można stosować tylko dla małych wartości m.
Trudności obliczeniowe związane z aproksymacją średniokwadratową za pomocą wielomianów wyższych stopni mogą być zmniejszone przy wykorzystaniu wielomianów ortogonalnych.
Dwie dowolne funkcje i nazywamy ortogonalnymi na zbiorze punk-tów: jeśli
![]()
(5.72)
przy czym:
![]()
(5.73)
Niech zbiór wielomianów:
(5.74)
będzie danym układem wielomianów ortogonalnych na zbiorze: , czyli
![]()
(5.75)
Po przedstawieniu wielomianu aproksymującego (5.71) w postaci kombinacji liniowej wielomianów układu (5.74)
(5.76)
odchylenie kwadratowe (5.66) przyjmuje postać
![]()
(5.77)
Podnosząc do kwadratu wyrażenie znajdujące się w nawiasie kwadratowym otrzymujemy
i następnie na mocy warunku ortogonalności (5.75), po wprowadzeniu oznaczeń:
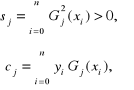
(5.78)
uzyskujemy
![]()
Uzupełniając wyrażenie znajdujące się w nawiasie pod znakiem pierwszej sumy do pełnego kwadratu
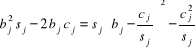
mamy
![]()
(5.79)
Wynika stąd, że średnie odchylenie kwadratowe S osiąga swą najmniejszą wartość dla współczynników
(5.80)
Szukany wielomian aproksymacyjny (5.76) ma więc postać
![]()
(5.81)
Dla układu równoodległych punktów: o stałej odległości h układ wielomianów ortogonalnych (5.74) tworzą wielomiany Grama [1, 25]
![]()
(5.82)
gdzie:
Pierwsze wielomiany Grama są następujące:
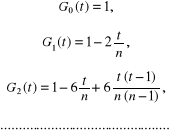
We wzorze aproksymującym (5.81) opartym na wielomianach Grama współczynnik (5.78a) jest określony zależnością
![]()
(5.83)
*
Aproksymacja średniokwadratowa danej funkcji ![]()
ciągłej w przedziale [a, b] polega na znalezieniu takiego ciągu współczynników ( j = 0, 1, ..., m), aby otrzymać minimum średniego odchylenia kwadratowego (5.62) dla funkcji określonej wzorem (5.65)
![]()
![]()
(5.84)
Podobnie jak w przypadku, gdy funkcja ![]()
była określona na dyskretnym zbiorze punktów obliczamy pochodne cząstkowe ( j = 0, 1, ..., m) i przyrównujemy je do zera. Otrzymany układ równań można również zapisać w postaci (5.67), w której iloczyny skalarne (5.68) wyrażone są za pomocą całek
![]()
(5.85)
Przy aproksymacji funkcji ciągłych wielomianami (5.71) występują te same problemy, jakie występowały przy aproksymacji funkcji określonych na dyskretnym zbiorze elementów. Oznacza to, że do aproksymacji średniokwadratowej funkcji ciągłej ![]()
można stosować tylko wielomiany niskich stopni.
Zadanie aproksymacji średniokwadratowej danej funkcji ciągłej ![]()
w danym przedziale [a, b] ma proste rozwiązanie, jeśli układ funkcji (4.6) wielomianu uogólnionego (5.65) jest ortogonalny.
Układ funkcji całkowalnych nazywamy ortogonalnym, jeśli
![]()
(5.86)
Liczbę
![]()
(5.87)
nazywamy normą funkcji w przedziale [a, b].
Jeśli normy wszystkich funkcji: są równe jedności, to układ ten nazywamy ortonormalnym. Układ ortonormalny spełnia więc następujące warunki
![]()
(5.88)
Dowolny układ , nie zawierający funkcji o normie równej zeru, można unormować dzieląc każdą funkcję przez jej normę
ponieważ jest
![]()
Na mocy warunku ortogonalności (5.86) wszystkie składniki lewej strony układu równań (5.67) leżące poza główną przekątną równają się zeru, a zatem
i ostatecznie otrzymujemy
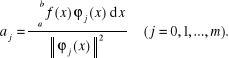
(5.89)
W przypadku układu ortonormalnego współczynniki wylicza się szczególnie łatwo, ponieważ wtedy
![]()
(5.90)
Współczynniki określone wzorem (5.89) nazywamy współczynnikami Fouriera funkcji ![]()
względem danego układu ortogonalnego Wielomian uogólniony ze współczynnikami Fouriera danej funkcji ma najmniejsze odchylenie kwadratowe od tej funkcji w porównaniu ze wszystkimi innymi wielomianami uogólnionymi tego samego stopnia m.
Układ ortogonalny w przedziale ![]()
tworzą wielomiany Legendre'a zdefiniowane wzorami (5.46), ponadto
![]()
(5.91)
Wynika stąd, że współczynniki (5.89) występujące w kombinacji liniowej wielomianów Legendre'a przybliżającej funkcję ![]()
w przedziale [1, 1] są następujące
![]()
(5.92)
W charakterze przykładu rozpatrzymy aproksymację funkcji ![]()
w prze-dziale ![]()
wielomianem stopnia piątego
(5.93)
Po obliczeniu ze wzorów (5.92) i (5.46) współczynników:
![]()
![]()
![]()
![]()
otrzymujemy
i ostatecznie mamy
![]()
Do aproksymacji używa się także układów funkcji ortogonalnych z wagą ![]()
będącą daną dodatnią funkcją ciągłą w przedziale ![]()
Warunek ortogonalności (5.88) ma wówczas postać
![]()
(5.94)
Przykładem układu funkcji ortogonalnego z wagą są wielomiany Czebyszewa (4.34) - znane również z tego, że w przedziale są one wielomianami najmniej odchylającymi się od zera [25]. Wielomiany Czebyszewa tworzą w przedziale ![]()
układ ortogonalny z funkcją wagową
![]()
czyli
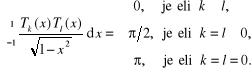
Każdą funkcję ciągłą w przedziale ![]()
można więc przybliżyć sumą szeregu
(5.95)
gdzie
![]()
Przykładowo aproksymując funkcję szeregiem (5.95) dla n = 3 [9]
uzyskujemy przybliżenie z błędem 0.00606.
*
{Program 5.2}
unit Obliczenia;
interface
uses
Windows, Messages, SysUtils, Classes, Graphics, Controls,
Forms, Dialogs, StdCtrls, Buttons, OleCtnrs;
const
mmax = 21;
type
Wekt1 = array[0..mmax] of Real;
Wekt2 = array[0..2*mmax] of Real;
Wekt3 = array[0..500] of Real;
Wekt4 = array[1..1000] of Real;
Tabl = array[1..mmax,1..mmax+1] of Real;
. . . . . . . . . . . . . . . . . . . . . .
var
Form3: TForm3;
i,j,k,n,m,Q,st,tr,war,X0,Y0,ZX,ZY: Integer;
a,b,bl,det,h,odch,x,y: Real;
xx,yy,Xekr,Yekr: Wekt4;
plik,plik1: Text;
xd,xp,yp: Wekt3;
aw,c,t: Wekt1;
am: Tabl;
s: Wekt2;
implementation
uses Ustawienia, Informacje, Grafika, Podglad;
{$R *.DFM}
function f(x: Real): Real;
begin
if Form3.RadioButton1.Checked then
f:=16*Sqr(x)*Sqr(x-1);
if Form3.RadioButton2.Checked then
f:=Abs(x);
if Form3.RadioButton3.Checked then
f:=1/(1+25*x*x);
if Form3.RadioButton4.Checked then
f:=100*x*x*Exp(-10*x);
end;
{procedure ElimGaussa(n,m: Integer; var A: Tabl; var det: Real);}
function Silnia(n: Integer): Real;
begin
if n=0 then Silnia:=1
else Silnia:=n*Silnia(n-1);
end;
function Komb(p,q: Integer): Real;
begin
Komb:=Silnia(p)/Silnia(q)/Silnia(p-q);
end;
function WCzyn(q: Real; j: Integer): Real;
var
k: Integer;
p: Real;
begin
p:=1;
if j>0 then
for k:=0 to j-1 do
p:=p*(q-k);
Wczyn:=p;
end;
function G(k,n: Integer; t: Real): Real;
var
s,p: Integer;
pom: Real;
begin
pom:=0; p:=-1;
for s:=0 to k do begin
if p=-1 then p:=1 else p:=-1;
pom:=pom+p*Komb(k,s)*Komb(k+s,s)*WCzyn(t,s)/WCzyn(n,s);
end;
G:=pom;
end;
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
procedure TForm3.BitBtn1Click(Sender: TObject);
begin
Form2.Show;
AssignFile(plik,Edit6.Text);
AssignFile(plik1,Edit5.Text);
Rewrite(plik); Rewrite(plik1);
if RadioButton5.Checked then war:=1;
if RadioButton6.Checked then war:=2;
Writeln(plik,'PROGRAM 5.2');
Writeln(plik,'Aproksymacja średniokwadratowa wielomianami.');
case war of
1: Writeln(plik,'Wielomian potęgowy.');
2: Writeln(plik,'Uogólniony wielomian Grama.');
end;
Writeln(plik);
a:=StrtoFloat(Edit1.Text); b:=StrtoFloat(Edit2.Text);
n:=StrtoInt(Edit3.Text); m:=StrtoInt(Edit4.Text);
Writeln(plik,'Początek przedziału: a = ',a:13);
Writeln(plik,'Koniec przedziału: b = ',b:13);
Writeln(plik,'Liczba punktów: n = ',n:3);
Writeln(plik,'Stopień wielomianu: m = ',m:3);
Writeln(plik1,n:3); Writeln(plik); h:=(b-a)/n;
for i:=0 to n do begin
x:=a+i*h; y:=f(x);
xp[i]:=x; yp[i]:=y;
xx[i+1]:=x; yy[i+1]:=y;
end;
Q:=n+2; xx[n+2]:=0; yy[n+2]:=0;
case war of
1: begin
t[0]:=0; s[0]:=n+1; xd:=xp;
for i:=0 to n do t[0]:=t[0]+yp[i];
for k:=1 to 2*m do begin
t[k]:=0; s[k]:=0;
for i:=0 to n do begin
if k<=m then t[k]:=t[k]+xd[i]*yp[i];
s[k]:=s[k]+xd[i];
xd[i]:=xd[i]*xp[i];
end;
end;
for i:=0 to m do begin
for j:=0 to m do am[i+1,j+1]:=s[i+j];
am[i+1,m+2]:=t[i];
end;
ElimGaussa(m+1,1,am,det);
for i:=0 to m do
aw[i]:=am[i+1,m+2];
end;
2: begin
for j:=0 to m do begin
s[j]:=0;
for i:=0 to n do
s[j]:=s[j]+Sqr(G(j,n,i));
end;
for j:=0 to m do begin
c[j]:=0;
for i:=0 to n do
c[j]:=c[j]+yp[i]*G(j,n,i);
end;
end;
end;
odch:=0;
Writeln(plik,'Wyniki aproksymacji funkcji:');
Writeln(plik,' i x[i] y[i] błąd');
for i:=0 to n do begin
x:=a+i*h;
case war of
1: begin
y:=aw[m];
for k:=m-1 downto 0 do
y:=y*x+aw[k];
end;
2: begin
y:=0;
for j:=0 to m do
y:=y+c[j]*G(j,n,i)/s[j];
end;
end;
bl:=f(x)-y; odch:=odch+Sqr(y-yp[i]);
Writeln(plik,i:3,' ',x:13,' ',y:18,' ',bl:13);
Q:=Q+1; xx[Q]:=x; yy[Q]:=y;
end;
Writeln(plik);
Writeln(plik,'Odchylenie kwadratowe: ',odch:13);
for k:=1 to 2*n+3 do
Writeln(plik1,xx[k]:13,' ',yy[k]:13);
CloseFile(plik); CloseFile(plik1);
Form2.Wyniki.Lines.LoadFromFile(Edit6.Text);
end;
. . . . . . . . . . . . . . . . . . . . . . .
procedure TForm3.BitBtn3Click(Sender: TObject);
begin
Close;
end;
end.
Program 5.2 jest przeznaczony do aproksymacji średniokwadratowej funkcji ![]()
określonej na dyskretnym zbiorze argumentów: W zależności od wyboru alternatywy obliczeń (rys. 5.9) funkcja aproksymująca przyjmowana jest albo w postaci wielomianu potęgowego (5.71), albo w postaci kombinacji liniowej wielomianów Grama: (5.76), (5.82). Ponadto z formularza Dane wczytywana jest także liczba m, określająca stopień wielomianu aproksymującego
Dane do programu 5.2, które dla dowolnych funkcji określonych na dyskretnych zbiorach argumentów mogą być również zapisywane w pliku Pr_5_2.dan, mają następujące znaczenie:
n - liczba zadanych punktów,
xp[0..n] - tablica zawierająca odcięte zadanych punktów,
yp[0..n] - tablica zawierająca zadane wartości funkcji w punktach:
Rys. 5.9
Tablica 5.1
|
Rys. |
Funkcja |
Wzór |
a |
b |
n |
m |
|
5.10 5.11 5.12 |
|
(5.71) (5.71) (5.76) |
−1 −1 −1 |
1 1 1 |
100 100 100 |
4 8 15 |
|
5.13 5.14 5.15 |
|
(5.71) (5.71) (5.76) |
−1 −1 −1 |
1 1 1 |
100 100 100 |
4 8 15 |
|
5.16 5.17 5.18 |
|
(5.71) (5.76) (5.76) |
0 0 0 |
1 1 1 |
100 100 100 |
4 8 15 |
Rys. 5.10
Rys. 5.11
Rys. 5.12
Rys. 5.13
Rys. 5.14
Rys. 5.15
Rys. 5.16
Rys. 5.17
Rys. 5.18
Program 5.2 działa podobnie jak programy 4.1 ÷ 4.6. Na ekranie monitora ukazuje się więc obraz wielomianu aproksymującego na tle zadanych punktów, oprócz tego do pliku Pr_5_2.wyn przesyłane są wyniki obliczeń zawierające w kolejnych wierszach: numer punktu i oraz wartości i Przykłady aproksymacji funkcji za pomocą uogólnionego wielomianu Grama (5.76) przedstawione zostały na rysunkach 5.10 ÷ 5.18, po wczytaniu kolejnych zestawów danych według tablicy 5.1.
Fragment tabulogramu wyników obliczeń numerycznych dotyczących aproksymacji średniokwadratowej funkcji ![]()
, przedstawionego na rysunku 5.15, jest następujący:
PROGRAM 5.2
Aproksymacja średniokwadratowa wielomianami.
Uogólniony wielomian Grama.
Początek przedziału: a = -1.0000E+0000
Koniec przedziału: b = 1.0000E+0000
Liczba punktów: n = 100
Stopień wielomianu: m = 15
Wyniki aproksymacji funkcji:
i x[i] y[i] błąd
0 -1.0000E+0000 2.518986064E-0002 1.3271E-0002
1 -9.8000E-0001 5.974592698E-0002 -1.9762E-0002
2 -9.6000E-0001 5.383489210E-0002 -1.2237E-0002
3 -9.4000E-0001 3.988067783E-0002 3.4281E-0003
4 -9.2000E-0001 3.154065954E-0002 1.3585E-0002
5 -9.0000E-0001 3.200026671E-0002 1.5058E-0002
6 -8.8000E-0001 3.939085206E-0002 9.7251E-0003
7 -8.6000E-0001 5.012419249E-0002 1.1841E-0003
8 -8.4000E-0001 6.076243538E-0002 -7.1144E-0003
9 -8.2000E-0001 6.889822648E-0002 -1.2750E-0002
10 -8.0000E-0001 7.340199295E-0002 -1.4578E-0002
11 -7.8000E-0001 7.429818159E-0002 -1.2607E-0002
12 -7.6000E-0001 7.245633913E-0002 -7.6895E-0003
13 -7.4000E-0001 6.922330766E-0002 -1.1497E-0003
14 -7.2000E-0001 6.607687193E-0002 5.5564E-0003
15 -7.0000E-0001 6.434662569E-0002 1.1125E-0002
16 -6.8000E-0001 6.502259447E-0002 1.4595E-0002
17 -6.6000E-0001 6.865449960E-0002 1.5449E-0002
18 -6.4000E-0001 7.533294160E-0002 1.3635E-0002
19 -6.2000E-0001 8.473691230E-0002 9.5138E-0003
20 -6.0000E-0001 9.622878985E-0002 3.7712E-0003
21 -5.8000E-0001 1.089773964E-0001 -2.7075E-0003
22 -5.6000E-0001 1.220910020E-0001 -8.9688E-0003
23 -5.4000E-0001 1.347447203E-0001 -1.4117E-0002
24 -5.2000E-0001 1.462900064E-0001 -1.7424E-0002
25 -5.0000E-0001 1.563375527E-0001 -1.8407E-0002
26 -4.8000E-0001 1.648084455E-0001 -1.6879E-0002
27 -4.6000E-0001 1.719517572E-0001 -1.2969E-0002
28 -4.4000E-0001 1.783296930E-0001 -7.0968E-0003
29 -4.2000E-0001 1.847737324E-0001 6.9151E-0005
30 -4.0000E-0001 1.923171173E-0001 7.6829E-0003
31 -3.8000E-0001 2.021101645E-0001 1.4809E-0002
32 -3.6000E-0001 2.153256437E-0001 2.0523E-0002
33 -3.4000E-0001 2.330614967E-0001 2.4008E-0002
34 -3.2000E-0001 2.562479099E-0001 2.4651E-0002
35 -3.0000E-0001 2.855650078E-0001 2.2127E-0002
36 -2.8000E-0001 3.213763803E-0001 1.6461E-0002
37 -2.6000E-0001 3.636824792E-0001 8.0647E-0003
38 -2.4000E-0001 4.120963730E-0001 -2.2603E-0003
39 -2.2000E-0001 4.658432112E-0001 -1.3354E-0002
40 -2.0000E-0001 5.237829567E-0001 -2.3783E-0002
41 -1.8000E-0001 5.844548896E-0001 -3.1969E-0002
42 -1.6000E-0001 6.461412592E-0001 -3.6385E-0002
43 -1.4000E-0001 7.069461243E-0001 -3.5805E-0002
44 -1.2000E-0001 7.648850572E-0001 -2.9591E-0002
45 -1.0000E-0001 8.179809354E-0001 -1.7981E-0002
46 -8.0000E-0002 8.643602460E-0001 -2.2913E-0003
47 -6.0000E-0002 9.023450931E-0001 1.5086E-0002
48 -4.0000E-0002 9.305358320E-0001 3.1003E-0002
49 -2.0000E-0002 9.478806214E-0001 4.2218E-0002
50 5.1159E-0013 9.537271490E-0001 4.6273E-0002
51 2.0000E-0002 9.478550127E-0001 4.2244E-0002
52 4.0000E-0002 9.304870864E-0001 3.1051E-0002
53 6.0000E-0002 9.022776003E-0001 1.5153E-0002
54 8.0000E-0002 8.642803436E-0001 -2.2114E-0003
55 1.0000E-0001 8.178960111E-0001 -1.7896E-0002
56 1.2000E-0001 7.648031433E-0001 -2.9509E-0002
57 1.4000E-0001 7.068748878E-0001 -3.5734E-0002
58 1.6000E-0001 6.460875295E-0001 -3.6331E-0002
59 1.8000E-0001 5.844243560E-0001 -3.1938E-0002
60 2.0000E-0001 5.237782462E-0001 -2.3778E-0002
61 2.2000E-0001 4.658651027E-0001 -1.3376E-0002
62 2.4000E-0001 4.121424962E-0001 -2.3064E-0003
63 2.6000E-0001 3.637496851E-0001 7.9975E-0003
64 2.8000E-0001 3.214575170E-0001 1.6380E-0002
65 3.0000E-0001 2.856515419E-0001 2.2041E-0002
66 3.2000E-0001 2.563322513E-0001 2.4567E-0002
67 3.4000E-0001 2.331334370E-0001 2.3936E-0002
68 3.6000E-0001 2.153791773E-0001 2.0470E-0002
69 3.8000E-0001 2.021385374E-0001 1.4781E-0002
70 4.0000E-0001 1.923187047E-0001 7.6813E-0003
71 4.2000E-0001 1.847461203E-0001 9.6763E-0005
72 4.4000E-0001 1.782747358E-0001 -7.0419E-0003
73 4.6000E-0001 1.718780503E-0001 -1.2895E-0002
74 4.8000E-0001 1.647245420E-0001 -1.6796E-0002
75 5.0000E-0001 1.562505145E-0001 -1.8319E-0002
76 5.2000E-0001 1.462139794E-0001 -1.7348E-0002
77 5.4000E-0001 1.346859364E-0001 -1.4058E-0002
78 5.6000E-0001 1.220630122E-0001 -8.9408E-0003
79 5.8000E-0001 1.089813953E-0001 -2.7115E-0003
80 6.0000E-0001 9.626135170E-0002 3.7386E-0003
81 6.2000E-0001 8.480854129E-0002 9.4422E-0003
82 6.4000E-0001 7.543290955E-0002 1.3535E-0002
83 6.6000E-0001 6.875434443E-0002 1.5349E-0002
84 6.8000E-0001 6.509431595E-0002 1.4523E-0002
85 7.0000E-0001 6.441560047E-0002 1.1056E-0002
. . . . . . . . . . . . . . . . . . . . . . . . . .
Odchylenie kwadratowe: 3.2997E-0002
304 5. Różniczkowanie, całkowanie i aproksymacja
5.4. Aproksymacja średniokwadratowa wielomianami 305
Wyszukiwarka