Inżynieria materiałowa (laboratoria IWN) |
Grupa dziekańska |
E1 |
|||
Temat: |
Badanie zależności zespolonej przenikalności elektrycznej dielektryków jonowych od temperatury |
Nr ćw. |
3 |
||
Imię i nazwisko |
|
Grupa laborat. |
2 |
||
Data wykonania: |
05.11.2009 |
Data oddania: |
19.11.2009 |
Ocena: |
|
1. Wprowadzenie teoretyczne
1.1 Dipole elektryczne
Dipolem nazywamy układ dwóch ładunków +q i -q ładunków tej samej wielkości, lecz przeciwnych znakach będących oddalonych o odległość l. Moment elektryczny o wartości ql skierowany jest od „-” do „+” jeżeli dipol umieścimy w jednorodnym polu elektrycznym ![]()
działają przeciwnie skierowane siły ![]()
obracające dipol wokół pkt. 0.
Rys.1 Moment sił dział. na dipol
Cząsteczki niektórych materiałów posiadają trwałe elektryczne momenty dipolowe. Indukowany moment dipolowy powstaje pod wpływem pola elektrycznego w skutek przesunięcia chmury elektronowej względem jądra lub atomów albo cząstek o ładunku o przeciwnych znakach.
1.2 Polaryzacja
Istnieją trzy mikroskopowe mechanizmy polaryzacji:
-polaryzacja elektronowa
-polaryzacja atomowa (jonowa)
-polaryzacja dipolowa (orientacji)
Istnieje jeszcze makroskopowy mechanizm polaryzacji, zachodzi gdy w materiale są wolne nośniki ładunku przemieszczające się w dielektryku.
1.3 Przenikalność elektryczna zespolona
Gdy między okładziny próżniowego kondensatora płaskiego umieścimy dielektryk to pojemność kondensatora wzrośnie o ΔC=C-C0. Podatność elektryczną wyraża się: ![]()
, jednak w praktyce stosuje się przenikalność elektryczną wzglądną: ![]()
,
jest częścią rzeczywistą przenikalności elektrycznej i określa zdolność magazynowania energii w materiale izolacyjnym. Zdolność rozpraszania energii przez materiał izolacyjny jest częścią urojoną przenikalności: ε'' stanowiącą straty energii na polaryzacje oraz prąd upływu.
W obwodzie prądu przemiennego przedstawiając związek pomiędzy napięciem i prądem, można posłużyć się zespoloną przenikalnością elektryczną. Gdy wprowadzimy do kondensatora dielektryk to wzrost pojemności pociągnie za sobą zmianę ładunku Δq=ΔCU, gdzie U=U0ejωt , ω=2πf, Δi=Δi0j(ωt+(π/2)) , Δi0=ωΔCU0 . Ze wzoru wynika że prąd wyprzedza w fazie napięcie o π/2, całkowity prąd: I0+ΔI=jωε'C0U.
Rys.2 Zależność miedzy U,I
W realnych układach występują straty związane z przewodnictwem (upływnością) i polaryzacją (dipolowo-relaksacyjne i absorpcyjne). Można zastosować więc schemat zastępczy z elementami idealnymi przedstawiający realny układ. Całkowity prąd będzie zatem równy I=I0+Δi+is , gdzie: is=U/R=ωε''C0. Wynika ze wzoru że ΔI=Δi+is=(jωΔC+G)U, G=1/R, kąt przesunięcia fazowego będzie mniejszy od π/2.
Rys.3 Schemat zastępczy
![]()
Kąt ψ dopełniający do π/2 jest kątem stratności dielektryka tgψ=is/Δi , zamiast tego stosuje się tangens kąta strat (współczynnik strat): ![]()
Dielektryki stałe o wiązaniach jonowych cząstek wykazują wzrost ε' wraz ze wzrostem temperatury. Straty ε” od T zależą od zmian oporów obrotu dipoli podczas zwiększania temperatury i od zmian przewodności. W wysokich temperaturach dominować będzie przewodność: σ = σ0eαT.
2. Zasada pomiaru i opis czynności
2.1 Zasada pomiaru
Badaną próbkę (szkło, porcelana) umieszczoną pomiędzy elektrodami pomiarowymi ustawiono na grzejniku sterowanym przez kontroler z czujnikiem temperatury PT100.
Dzięki czemu można ustawić podgrzewanie do żądanej Tmax. Pomiar pojemności i współczynnika strat dielektrycznych dokonuje się za pomocą mostka Scheringa.
Rys.4 Schemat mostka Scheringa
W stanie równowagi mostka zachodzi zależność: ![]()
R4 jest tak dobrane że: R4 = 1000/π = 318,3Ω wtedy zachodzi uproszczenie: tgδ = 0,1*C4 ,
Gdzie C4 podane jest w μF. Przy maksymalnej czułości mostka uchyb pomiaru opisany jest wzorami: ![]()
Uchyb pomiaru w obu przypadkach jest mniejszy od 0,2%, jednak po uwzględnieniu nieczułości mostka, napięcia progowego wskaźnika równowagi, uchyb współczynnika strat jest procentowo większy od uchybu pomiaru pojemności. Najmniejszą wartość uchybu warunkują także połączenia mostka (mające pojemność, rezystancje, indukcyjność). Na tablicach podany jest uchyb względny w procentach i najmniejsza wartość uchybu bezwzględnego. Stan równowagi mostka dla prądu przemiennego nie jest zależny tylko od elementów mostka, ale także od pojemności cząstkowych w układzie.
2.2 Czynności:
1. Ustawienie na autotransformatorze napięcia 40V
2. Ustawianie temperatury 80°C na kontrolerze
3. Załączenie źródła napięcia probierczego i ustawienie napięcia pomiarowego 2kV
4. Równoważenie mostka co 5°C z wyłączeniem zasilania grzałki przy odczycie/zapisie R3, R4, C4, T
5. Zapis wymiarów geometrycznych próbki oraz Cw.
3. Obliczenia tablice wykresy
3.1 Wzory obliczeniowe
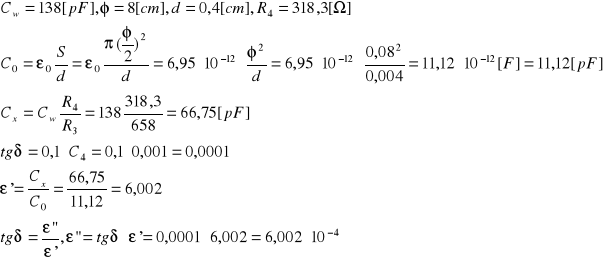
3.2 Tabela pomiarowo-obliczeniowa
L.p. |
T |
R3 |
C4 |
R4 |
Cw |
d |
Φ |
Co |
Cx |
tgδ |
ε' |
ε" |
|
[°C] |
[Ω] |
[μF] |
[Ω] |
[pF] |
[m] |
[m] |
[pF] |
[pF] |
|
|
|
1 |
20 |
658 |
0,001 |
318,3 |
138 |
0,004 |
0,08 |
11,12 |
66,75 |
0,0001 |
6,002 |
0,0006002 |
2 |
25 |
658 |
0,001 |
318,3 |
138 |
0,004 |
0,08 |
11,12 |
66,75 |
0,0001 |
6,002 |
0,0006002 |
3 |
30 |
659 |
0,001 |
318,3 |
138 |
0,004 |
0,08 |
11,12 |
66,65 |
0,0001 |
5,993 |
0,0005993 |
4 |
35 |
659 |
0,001 |
318,3 |
138 |
0,004 |
0,08 |
11,12 |
66,65 |
0,0001 |
5,993 |
0,0005993 |
5 |
40 |
659 |
0,002 |
318,3 |
138 |
0,004 |
0,08 |
11,12 |
66,65 |
0,0002 |
5,993 |
0,0011986 |
6 |
45 |
659 |
0,002 |
318,3 |
138 |
0,004 |
0,08 |
11,12 |
66,65 |
0,0002 |
5,993 |
0,0011986 |
7 |
50 |
658 |
0,002 |
318,3 |
138 |
0,004 |
0,08 |
11,12 |
66,75 |
0,0002 |
6,002 |
0,0012005 |
8 |
55 |
658 |
0,002 |
318,3 |
138 |
0,004 |
0,08 |
11,12 |
66,75 |
0,0002 |
6,002 |
0,0012005 |
9 |
60 |
657 |
0,001 |
318,3 |
138 |
0,004 |
0,08 |
11,12 |
66,85 |
0,0001 |
6,011 |
0,0006011 |
10 |
65 |
656 |
0,004 |
318,3 |
138 |
0,004 |
0,08 |
11,12 |
66,95 |
0,0004 |
6,020 |
0,0024083 |
11 |
70 |
656 |
0,006 |
318,3 |
138 |
0,004 |
0,08 |
11,12 |
66,95 |
0,0006 |
6,020 |
0,0036125 |
12 |
75 |
655 |
0,015 |
318,3 |
138 |
0,004 |
0,08 |
11,12 |
67,06 |
0,0015 |
6,030 |
0,0090450 |
13 |
80 |
654 |
0,017 |
318,3 |
138 |
0,004 |
0,08 |
11,12 |
67,16 |
0,0017 |
6,039 |
0,0102667 |
3.3 Wykresy
3.3.1 Wykres zależności części rzeczywistej przenikalności w funkcji temperatury
3.3.2 Wykres zależności części urojonej przenikalności w funkcji temperatury
3.3.3 Wykres zależności współczynnika strat w funkcji temperatury
3.3.4 Wykres zależności pojemności Cx w funkcji temperatuy
4. Wnioski końcowe
1. Względna przenikalność elektryczna po przekroczeniu 45°C wzrasta w przybliżeniu proporcjonalnie względem temperatury,
2. Straty energii w dielektryku wzrastają dopiero po przekroczeniu temperatury 60°C, wzrost jest wykładniczy względem temperatury zgodnie z wymienionym wzorem σ = σ0eαT,
3. Zgodnie z definicją współczynnik strat w podobny sposób wzrasta względem temperatury, z zależnością wykładniczą po przekroczeniu 60°C,
4. Wartość pojemności Cx wzrasta podobnie jak w przypadku względnej przenikalności elektrycznej po przekroczeniu temperatury 45°C w przybliżeniu liniowo.
5. Parametry nie zmieniają się znacząco przy różnicy temperatury 20-40°C powyżej temperatury pokojowej (20°C), dopiero po przekroczeniu 60°C widać wyraźny wzrost parametrów
6. W małych temperaturach straty są rzędu dziesiątek tysięcznych części ułamka w porównaniu do przenikalności elektrycznej jest to 10000 razy mniej,
7. Przy temperaturze 80°C różnica pomiędzy względną przenikalnością a stratami w dielektryku wynosi już tylko: ok. 600 razy mniej,
8. Względna przenikalność wynosząca ok. 6 wskazuje na materiał dielektryka: szkło lub porcelana, w praktyce waha się od kilku do kilkunastu
9. Podczas równoważenia mostka należy wyłączyć grzałkę ponieważ podłączona grzałka wytwarza pole elektryczne które wpływa w znaczącym stopniu na wyniki pomiaru
10. Wartości pomiarów i obliczeń ze względu na precyzje <0,2% należy ograniczyć do 4 liczb znaczących
11. Zespolona przenikalność wzrasta w funkcji temperatury, ponieważ część rzeczywista i urojona także wzrastają w funkcji T, rzeczywista (przenikalność elektryczna względna) z przybliżoną zależnością liniową a urojona (straty energii) z wykładniczą.
Wyszukiwarka