1.Cel ćwiczenia:
Celem ćwiczenia było zapoznanie się zespołu z budową i zasadą działania licznika Geigera-Mullera i wykazanie, że częstość przemian promieniotwórczych jest funkcją statystyczną, której gęstość prawdopodobieństwa wyrażona jest jako:
a/ rozkład Poissona, w przypadku małych wartości częstości,
b/ rozkład Gaussa, gdy wartości częstości są duże.
W części pomiarowej ćwiczenia dokonano pomiarów napięcia licznika i opowiadającej mu szybkości zliczania impulsów w celu wyznaczenia charakterystyki roboczej licznika. Wykonano również pomiary szybkości zliczania impulsów dla dwóch próbek promieniotwórczych razem oraz dla każdej z osobna. Posłużyło to następnie do obliczenia czasu martwego licznika. Zgodność rozpadu promieniotwórczego z rozkładem Poissona została zbadana przy pomocy testu χ2 na zautomatyzowanym ( komputer ) stanowisku pomiarowym.
Schemat blokowy aparatury pomiarowej przedstawia poniższy rysunek
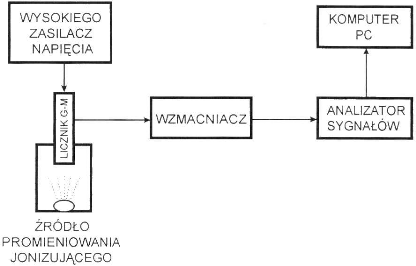
2.Pomiary
A.Wyznaczenie charakterystyki roboczej licznika Geigera-Mullera
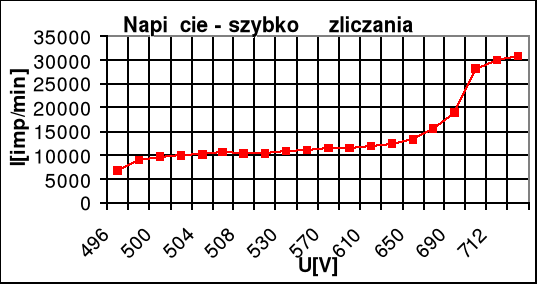
W pierwszej części ćwiczenia wyznaczaliśmy charakterystykę roboczą licznika. W tym celu dokonaliśmy pomiarów, na podstawie których można ją narysować.
U[V] |
N[imp] |
I[imp/min] |
sigma |
496 |
6741 |
6741 |
82,10359 |
498 |
9087 |
9087 |
95,32576 |
500 |
9627 |
9627 |
98,11728 |
502 |
9938 |
9938 |
99,68952 |
504 |
10153 |
10153 |
100,7621 |
506 |
10506 |
10506 |
102,4988 |
508 |
10459 |
10459 |
102,2693 |
510 |
10430 |
10430 |
102,1274 |
530 |
10832 |
10832 |
104,0769 |
550 |
11170 |
11170 |
105,6882 |
570 |
11453 |
11453 |
107,0187 |
590 |
11509 |
11509 |
107,28 |
610 |
11952 |
11952 |
109,3252 |
630 |
12482 |
12482 |
111,7229 |
650 |
13212 |
13212 |
114,9435 |
670 |
15535 |
15535 |
124,6395 |
690 |
19010 |
19010 |
137,8768 |
710 |
28123 |
28123 |
167,6991 |
712 |
30098 |
30098 |
173,4878 |
720 |
31022 |
31022 |
176,1306 |
Gdzie:
U[V] - napięcie między katodą a anodą licznika
N[imp] - ilość zliczonych impulsów podczas pomiarów (t=1min)
I[imp/min] - szybkość zliczania impulsów
Sigma=![]()
Na podstawie wykresu możemy określić podstawowe parametry licznika:
Napięcie progowe: Up=496 [V]
Napięcie U1=506[V]
Napięcie U2=578[V]
Napięcie pracy: U=542 [V]
Długość plateau: 72 [V]
Nachylenie plateau:12,57%
Zmierzyliśmy również tło licznika: I = 12 [imp/min]
B. Czas martwy licznika Geigera-Mullera
Dalsza część ćwiczenia miała na celu określenie czasu martwego badanego licznika, który jest głównym czynnikiem ograniczającym szybkość zliczania impulsów. Opieraliśmy się na pomiarze aktywności dwóch próbek osobno i razem.
Nr. preparatu |
t [min] |
N [imp] |
In [imp/min] |
I = In-Itła |
1 |
10 |
113533 |
11353 |
11341 |
1+2 |
10 |
252845 |
25285 |
25273 |
2 |
10 |
144525 |
14453 |
14441 |
Wartość czasu martwego mogę wyznaczyć korzystając z przybliżonej zależności. Została ona wyprowadzona w oparciu o równanie, które stwierdza równość między rzeczywistą aktywnością obu próbek jednocześnie i sumą rzeczywistych aktywności każdej z próbek z osobna. Wyniki pomiarów aktywności przy pomocy licznika Geigera-Mullera stwierdzają brak takiej zgodności w przypadku aktywności zmierzonych. Wynika ona z tego, że pomiar aktywności obarczony jest błędem wynikającym z istnienia czasu martwego. Czas martwy powoduje, że przy pomiarze większych aktywności pominięta zostanie większa liczba cząstek, które powinny wzbudzić licznik i wywołać zliczenie kolejnego impulsu, niż przy pomiarze mniejszych aktywności. Spowodowane jest to tym, że cząstki są częściej wysyłane i częściej trafiają na licznik w `stanie martwym'. Dlatego zmierzona aktywność połączonych próbek jest mniejsza niż suma zmierzonych aktywności obu próbek z osobna. Znając zależność między intensywnością rzeczywistą, a intensywnością zmierzoną i czasem martwym licznika można dojść do zależności:
τ = ( I1 + I2 - I1,2 ) / 2I1I2
gdzie:
τ - czas martwy licznika;
I1 -zmierzona intensywność pierwszej próbki;
I2 -zmierzona intensywność drugiej próbki;
I1,2 - zmierzona intensywność obu próbek razem;
τ = 1.55 [ μs ];
Błąd wyznaczenia czasu martwego licznika wyznaczam metodą różniczki zupełnej:
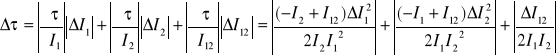
Przy czym błędy zliczania impulsów wyznaczam z zależności:
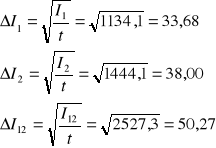
Zatem błąd wyznaczenia czasu martwego:
![]()
Ostatecznie więc wyznaczony przez nas czas martwy licznika wynosi:
τ = 1,55 ± 0,36 [μs]
Charakterystyka U - I badanego przez nas licznika ma spodziewany przebieg. Obszar `plateau' charakteryzuje się względnie dużym pochyleniem ( rzędu 13 % ), co sprawia, że w obszarze pracy licznik podaje różne wartości zliczonych impulsów podczas zmian napięcia pracy. Długość obszaru `plateau', która nie jest zbyt duża (72 [V]) także świadczy o niezbyt wysokiej klasie licznika. Na końcu obszaru `plateau' charakterystyka rośnie parabolicznie względnie łagodnie, co spowodowane jest wzrostem prawdopodobieństwa wyładowania samoistnego.
Zmierzone promieniowanie tła, które wynosiło Itła = 12 [imp/min], jest nieznaczne w porównaniu do promieniowania badanego, preparatu promieniotwórczego i w znikomy sposób mogło wpłynąć na uzyskane wyniki.
C. Badanie statystycznego charakteru rozpadu promieniotwórczego
Aby wyznaczyć własności statystyczne rozpadu promieniotwórczego rejestrowaliśmy w krótkich odcinkach czasu impulsy pochodzące z licznika Geigera - Mullera. Krótkie chwile czasu w których następowało zliczanie spowodowały losowy rozrzut uzyskanych stanów przelicznika. Gdyby czas pojedynczych pomiarów był długi to uzyskiwane stany przelicznika byłyby bardzo zbliżone co uniemożliwiałoby analizę statystyczną. Wyniki pomiarów zostały zarejestrowane w postaci histogramów dla dwóch serii pomiarowych:
seria 1 - ilość wartości zmiennej losowej 650 przy wartości średniej rozkładu
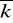
=7;seria 2 - ilość wartości zmiennej losowej 650 przy wartości średniej rozkładu
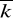
=26;
Histogram te zostały ponadto opisane tabelarycznie.
Dla wartości oczekiwanej zmiennej losowej ![]()
< 20 (poziom ufności 99,5%) zarejestrowany rozpad promieniotwórczy podlega rozkładowi Poissona Dla wartości oczekiwanej zmiennej losowej ![]()
> 20 zarejestrowany rozpad promieniotwórczy podlega rozkładowi Gaussa. Za pomocą testu χ2 określiłem zgodność otrzymanych wyników z danym rozkładem. Poszczególne etapy obliczeń zostały zebrane w poniższych tabelach:
Seria pomiarowa 1:
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
kj |
n(kj) |
ki*n(kj) |
ki-k |
(ki-k)2 |
Pk(ki) |
Pk,k(ki) |
n*Pk(ki) |
n*Pk,k(ki) |
nj-n*Pk(ki) |
nj-n*Pk,k(ki) |
|
|
0 |
2 |
0 |
-17 |
289 |
0,0009119 |
1,035E-09 |
0,5927233 |
6,726E-07 |
1,4072767 |
1,9999993 |
3,341235 |
6,7485072 |
1 |
4 |
4 |
-16 |
256 |
0,0063832 |
9,339E-09 |
4,1490629 |
6,07E-06 |
-0,149063 |
3,9999939 |
0,0053554 |
3,8562807 |
2 |
20 |
40 |
-15 |
225 |
0,0223411 |
7,376E-08 |
14,52172 |
4,795E-05 |
5,4782797 |
19,999952 |
2,0666662 |
27,544814 |
3 |
47 |
141 |
-14 |
196 |
0,0521293 |
5,099E-07 |
33,884014 |
0,0003314 |
13,115986 |
46,999669 |
5,0769985 |
65,192065 |
4 |
62 |
248 |
-13 |
169 |
0,0912262 |
3,085E-06 |
59,297025 |
0,002005 |
2,7029754 |
61,997995 |
0,1232115 |
64,821994 |
5 |
76 |
380 |
-12 |
144 |
0,1277167 |
1,633E-05 |
83,015834 |
0,0106155 |
-7,015834 |
75,989384 |
0,5929222 |
69,557652 |
6 |
122 |
732 |
-11 |
121 |
0,1490028 |
7,567E-05 |
96,851807 |
0,049188 |
25,148193 |
121,95081 |
1,5298898 |
153,55419 |
7 |
91 |
637 |
-10 |
100 |
0,1490028 |
0,0003069 |
96,851807 |
0,1994673 |
-5,851807 |
90,800533 |
0,3535674 |
85,127341 |
8 |
80 |
640 |
-9 |
81 |
0,1303774 |
0,0010891 |
84,745331 |
0,70791 |
-4,745331 |
79,29209 |
0,2657157 |
74,189757 |
9 |
56 |
504 |
-8 |
64 |
0,1014047 |
0,0033827 |
65,913035 |
2,198763 |
-9,913035 |
53,801237 |
1,4908776 |
43,915033 |
10 |
46 |
460 |
-7 |
49 |
0,0709833 |
0,0091952 |
46,139125 |
5,9768576 |
-0,139125 |
40,023142 |
0,0004195 |
34,717866 |
11 |
25 |
275 |
-6 |
36 |
0,0451712 |
0,021875 |
29,361261 |
14,218751 |
-4,361261 |
10,781249 |
0,6478127 |
3,9587986 |
12 |
9 |
108 |
-5 |
25 |
0,0263498 |
0,045544 |
17,127402 |
29,60357 |
-8,127402 |
-20,60357 |
0,8566659 |
24,785258 |
13 |
8 |
104 |
-4 |
16 |
0,0141884 |
0,0829865 |
9,2224474 |
53,941221 |
-1,222447 |
-45,94122 |
0,162037 |
228,85419 |
14 |
1 |
14 |
-3 |
9 |
0,0070942 |
0,1323361 |
4,6112237 |
86,018434 |
-3,611224 |
-85,01843 |
2,8280859 |
1567,5089 |
15 |
1 |
15 |
-2 |
4 |
0,0033106 |
0,1846898 |
2,1519044 |
120,04839 |
-1,151904 |
-119,0484 |
0,6166091 |
6586,0362 |
120 |
650 |
4302 |
|
1784 |
|
|
|
|
|
|
19,958069 |
9040,3688 |
7,5 |
|
|
|
111,5 |
|
|
|
|
|
|
Poisson |
Gauss |
|
|
|
|
(k)2 |
|
|
|
|
|
|
|
|
Dla rozkładu Poissona *2 = 20
Dla rozkładu Gaussa *2 = 9040
Seria pomiarowa 2:
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
12 |
1 |
12 |
-14 |
196 |
0,0010179 |
0,0355105 |
0,6616069 |
23,081853 |
0,3383931 |
-22,08185 |
0,1730784 |
737,00597 |
13 |
0 |
0 |
-13 |
169 |
0,0020357 |
0,0427523 |
1,3232138 |
27,788972 |
-1,323214 |
-27,78897 |
1,3232138 |
583,59954 |
14 |
0 |
0 |
-12 |
144 |
0,0037806 |
0,050768 |
2,4573971 |
32,999229 |
-2,457397 |
-32,99923 |
2,4573971 |
443,1311 |
15 |
2 |
30 |
-11 |
121 |
0,0065531 |
0,0594636 |
4,2594884 |
38,651343 |
-2,259488 |
-36,65134 |
1,1985683 |
315,37143 |
16 |
6 |
96 |
-10 |
100 |
0,0106487 |
0,0686976 |
6,9216686 |
44,653436 |
-0,921669 |
-38,65344 |
0,1227266 |
215,85664 |
17 |
7 |
119 |
-9 |
81 |
0,0162863 |
0,0782819 |
10,586081 |
50,88323 |
-3,586081 |
-43,88323 |
1,2148007 |
181,91225 |
18 |
23 |
414 |
-8 |
64 |
0,0235246 |
0,0879854 |
15,291006 |
57,190509 |
7,7089936 |
-34,19051 |
0,8865056 |
76,449572 |
19 |
22 |
418 |
-7 |
49 |
0,0321916 |
0,0975415 |
20,924535 |
63,401969 |
1,0754649 |
-41,40197 |
0,055276 |
81,919288 |
20 |
24 |
480 |
-6 |
36 |
0,0418491 |
0,106659 |
27,201896 |
69,328375 |
-3,201896 |
-45,32838 |
0,3768905 |
75,533765 |
21 |
14 |
294 |
-5 |
25 |
0,0518131 |
0,1150364 |
33,678537 |
74,773687 |
-19,67854 |
-60,77369 |
2,4982676 |
109,6675 |
22 |
44 |
968 |
-4 |
16 |
0,0612337 |
0,1223778 |
39,801908 |
79,545582 |
4,1980921 |
-35,54558 |
0,4427923 |
31,744418 |
23 |
53 |
1219 |
-3 |
9 |
0,0692207 |
0,1284102 |
44,993461 |
83,46662 |
8,0065389 |
-30,46662 |
1,4247552 |
20,629997 |
24 |
61 |
1464 |
-2 |
4 |
0,0749891 |
0,1329002 |
48,742916 |
86,38515 |
12,257084 |
-25,38515 |
3,0822141 |
13,220502 |
25 |
60 |
1500 |
-1 |
1 |
0,0779887 |
0,1356693 |
50,692633 |
88,185026 |
9,3073672 |
-28,18503 |
1,7088693 |
15,670831 |
26 |
41 |
1066 |
0 |
0 |
0,0779887 |
0,136605 |
50,692633 |
88,79328 |
-9,692633 |
-47,79328 |
2,8532699 |
45,059755 |
27 |
49 |
1323 |
1 |
1 |
0,0751002 |
0,1356693 |
48,815128 |
88,185026 |
0,1848721 |
-39,18503 |
0,0007001 |
31,454721 |
28 |
48 |
1344 |
2 |
4 |
0,0697359 |
0,1329002 |
45,328333 |
86,38515 |
2,671667 |
-38,38515 |
0,1574689 |
32,505491 |
29 |
45 |
1305 |
3 |
9 |
0,0625218 |
0,1284102 |
40,639195 |
83,46662 |
4,3608049 |
-38,46662 |
0,4679379 |
36,410192 |
30 |
31 |
930 |
4 |
16 |
0,0541856 |
0,1223778 |
35,220636 |
79,545582 |
-4,220636 |
-48,54558 |
0,5057764 |
66,911726 |
31 |
30 |
930 |
5 |
25 |
0,045446 |
0,1150364 |
29,539888 |
74,773687 |
0,4601119 |
-44,77369 |
0,0071667 |
67,863596 |
32 |
24 |
768 |
6 |
36 |
0,0369249 |
0,106659 |
24,001159 |
69,328375 |
-0,001159 |
-45,32838 |
5,597E-08 |
85,606765 |
33 |
19 |
627 |
7 |
49 |
0,0290923 |
0,0975415 |
18,910004 |
63,401969 |
0,0899959 |
-44,40197 |
0,0004283 |
104,25883 |
34 |
18 |
612 |
8 |
64 |
0,0222471 |
0,0879854 |
14,460591 |
57,190509 |
3,5394086 |
-39,19051 |
0,866314 |
106,21253 |
35 |
8 |
280 |
9 |
81 |
0,0165264 |
0,0782819 |
10,742154 |
50,88323 |
-2,742154 |
-42,88323 |
1,6999906 |
171,19206 |
36 |
9 |
324 |
10 |
100 |
0,0119357 |
0,0686976 |
7,758222 |
44,653436 |
1,241778 |
-35,65344 |
0,1987585 |
163,84779 |
37 |
3 |
111 |
11 |
121 |
0,0083873 |
0,0594636 |
5,4517236 |
38,651343 |
-2,451724 |
-35,65134 |
1,1025777 |
233,14063 |
38 |
6 |
228 |
12 |
144 |
0,0057387 |
0,050768 |
3,7301267 |
32,999229 |
2,2698733 |
-26,99923 |
1,3812734 |
195,42456 |
39 |
0 |
0 |
13 |
169 |
0,0038258 |
0,0427523 |
2,4867511 |
27,788972 |
-2,486751 |
-27,78897 |
2,4867511 |
310,5365 |
40 |
0 |
0 |
14 |
196 |
0,0024868 |
0,0355105 |
1,6163882 |
23,081853 |
-1,616388 |
-23,08185 |
1,6163882 |
329,60643 |
41 |
1 |
41 |
15 |
225 |
0,001577 |
0,0290928 |
1,0250267 |
18,910298 |
-0,025027 |
-17,9103 |
0,000611 |
312,94675 |
795 |
649 |
16903 |
|
2255 |
|
|
|
|
|
|
31,310768 |
5194,6911 |
|
|
|
|
72,74 |
|
|
|
|
|
|
Poisson |
Gauss |
|
|
|
|
(k)2 |
|
|
|
|
|
|
|
|
Dla rozkładu Poissona *2 = 31,31
Dla rozkładu Gaussa *2 = 5194,7
Wnioski
Zestawienie wyników
Rozkład doświadczalny |
N=650 r=16 ksr=7 |
N=650 r=31 ksr=26
|
|
Rozkład Poissona |
sp= r-2 =14 *p2= 20 *gr2= 31,32 |
sp.= r-2 =29 *p2=31,31 *gr2=52,34 |
|
Rozkład Gaussa
|
sG= r-3 =13 *G2=9040,37 *gr2=29,82 |
SG= r-3 =28 *G2= 5194,69 *gr2=50,99 |
|
. Prawdopodobieństwo w rozkładzie dwumianowym określone przez trzy parametry: czas obserwacji t, stałą przemiany λ, oraz ilość atomów N. W praktycznych badaniach nie jesteśmy w stanie dokładnie określić liczby atomów w próbce stąd stosujemy dwie aproksymacje rozkładu dwumianowego: rozkład Poissona ( gdy średnia liczba przemian jest mała) oraz rozkład normalny czyli rozkład Gaussa ( gdy średnia liczba przemian jest duża).
Warto się zastanowić jaki rozkład teoretyczny dobrze opisuje rozkład doświadczalny zmiennej losowej, gdzie zmienna losową jest liczba przemian jąder w preparacie promieniotwórczym w określonym czasie . Wiadomo ,źe jeżeli liczba k będzie większa od 20 to dane zjawisko dobrze opisuje rozkład Gaussa, w przeciwnym przypadku rozkład opisuje rozkład Poissona. Wartości liczby *2 dla rozkładu Poissona dla obu przeprowadzonych serii przybiera wartości odpowiednio 20 oraz 31 (obie wartości są mniejsze od *gr2), podczas, gdy liczby te w rozkładzie Gaussa przybierają wartości kilku tysięcy. Zatem słuszne jest stwierdzenie mówiące, że rozpady promieniotwórcze opisuje rozkład Poissona.
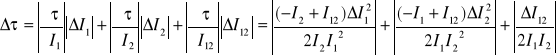
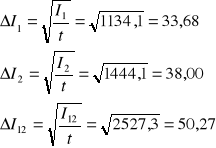
![]()
Wyszukiwarka