WIP, ZIP, gr. 2

SPRAWOZDANIE

Z LABORATORIUM TECHNIKI CIEPLNEJ

Badanie przepływów płynów.

Wyznaczanie współczynnika lepkości cieczy.

Wykonali:

Chędoszko Arkadiusz

Olszewski Jakub

Pietruczuk Marcin

Pleńska Aneta

Podniesińska Martyna

Rojek Katarzyna

Rybacki Iwo

Szostek Anna

Wprowadzenie teoretyczne:

Przepływ to opis ruchu płynu, podstawowe pojęcie z zakresu kinematyki płynów.

W ujęciu ogólnym przepływ można scharakteryzować tzw. metodą Eulera przez podanie pola prędkości płynu, czyli zależności prędkości od współrzędnych przestrzennych i czasu.

Cieczą doskonałą nazywamy ciecz nieściśliwą, nielepką, inaczej: płyn idealny.

Pojęcie to stosuje się w hydrodynamice i aerodynamice do opisu laminarnych przepływów, przy dużych liczbach Reynoldsa.

Płyny rzeczywiste mają zdolność przyczepiania się do ścian przewodów, przez które przepływają lub też do przedmiotów, wokół których opływają. Zdolność ta nazywa się lepkością. Lepkość to opór wewnętrzny przeciw płynięciu. Lepkością nie jest opór przeciw płynięciu powstający na granicy płynu i ścianek naczynia. Lepkość jest jedną

z najważniejszych cech olejów.

Zgodnie z laminarnym modelem przepływu lepkość wynika ze zdolności płynu do przekazywania pędu pomiędzy warstwami poruszającymi się z różnymi prędkościami.

Różnice w prędkościach warstw są charakteryzowane w modelu laminarnym przez szybkość ścinania. Przekazywanie pędu zachodzi dzięki pojawieniu się na granicy tych warstw naprężeń ścinających. Wspomniane warstwy są pojęciem hipotetycznym, w rzeczywistości zmiana prędkości zachodzi w sposób ciągły, a naprężenia można określić w każdym punkcie płynu. Model laminarny lepkości zawodzi też przy przepływie turbulentnym, powstający np. na granicy płynu i ścianek naczynia.

Dla przepływu turbulentnego jak dotąd nie istnieją dobre modele teoretyczne.

Płyn nielepki to płyn o zerowej lepkości.

Istnieją dwie miary lepkości:

Lepkość dynamiczna wyrażająca stosunek naprężeń ścinających do szybkości ścinania:

Jednostką lepkości dynamicznej w układzie SI jest: kilogram·metr^-1·sekunda^-1

Lepkość kinematyczna czasami nazywana też kinetyczną jest stosunkiem

lepkości dynamicznej do gęstości płynu:

Jednostką lepkości kinematycznej w układzie SI jest: metr²·sekunda^-1

Jej nazwa pochodzi od tego, że jest wyrażona jedynie przez wielkości właściwe kinematyce.

Rodzaje przepływów

• Przepływ stacjonarny (ustalony) jest pojęciem uproszczonym zakładającym,

że przepływ w każdym punkcie obszaru zajętego przez ciecz nie zmienia się w czasie. Przy takim założeniu równania opisujące ruch płynu (Naviera-Stokesa i ciągłości przepływu) przybierają prostsze formy.

Podstawową zależnością opisującą wpływ sił na ruch płynu jest równanie Naviera-Stokesa.

gdzie: v - prędkość, b - siły masowe (np. grawitacja), ρ - gęstość płynu, p - ciśnienie,

ν - lepkość kinematyczna płynu

Lewa strona równia jest pochodną substancjalną prędkości płynu.

• Przepływ laminarny (warstwowy) jest pojęciem stosowanym do określenia przypadku, gdy strumień stanowi zespół warstw przemieszczających się jedna względem drugiej bez ich mieszania, a prędkość w każdym punkcie jest jednoznacznie określona. Przy małych prędkościach przepływ cieczy przez gładką rurę jest laminarny, a ze względu na lepkość największa prędkość przepływu jest w środku - wzdłuż osi przekroju podłużnego rury.

• Przepływ turbulentny (wirowy) jest określeniem ruchu warstw cieczy,

podczas którego prędkość maksymalna przepływu cieczy przekroczy pewną charakterystyczną dla danego płynu wartość "krytyczną". Następuje wtedy mieszanie cieczy, w efekcie czego powstają wiry- stąd też określenie przepływu turbulentnego, który ze swej natury jest zmienny w czasie. Prędkość przestaje wtedy być wtedy prostą funkcją współrzędnych położenia.

Możliwe jest wprowadzenie uśrednionych wartości opisujących przepływ, a także średnich kwadratowych wartości ich odchyleń. Podejście to znacznie komplikuje równania przepływu. Jest też możliwe w przypadku turbulentnego przepływu nieustalonego.

W przypadku płynu nielepkiego i przepływu bezwirowego, przepływ ustalony nosi nazwę przepływu potencjalnego ponieważ pole prędkości jest wtedy polem potencjalnym.

Równanie Bernoullego opisuje parametry płynu doskonałego płynącego w rurze (niekoniecznie materialnie istniejącej) o zmiennym przekroju. Wynika ono wprost z faktu zachowania objętości cieczy doskonałej (która jest nieściśliwa) i zasady zachowania energii mechanicznej.

Założenia:

• ciecz jest nieściśliwa

• ciecz nie jest lepka

• przepływ stacjonarny i bezwirowy

gdzie:

• E - energia jednostki masy płynu

• ρ - gęstość cieczy

• v - prędkość cieczy w rozpatrywanym miejscu

• h - wysokość w układzie odniesienia, w którym liczona jest energia potencjalna

• g - przyspieszenie grawitacyjne

• p - ciśnienie cieczy w rozpatrywanym miejscu

Poszczególne człony to: energia kinetyczna, energia potencjalna przyciągania ziemskiego, energia ciśnienia.

Energia jest stała tylko wówczas, kiedy element porusza się wzdłuż linii prądu.

Istnienie lepkości lub przepływu wirowego rozprasza energię, ściśliwość zmienia zależność prędkości przepływu od ciśnienia. Niestacjonarność przepływu wiąże się z dodatkowym ciśnieniem rozpędzającym lub hamującym ciecz.

Z równania Bernoullego dla sytuacji przedstawionej na rysunku zachodzi prawidłowość:

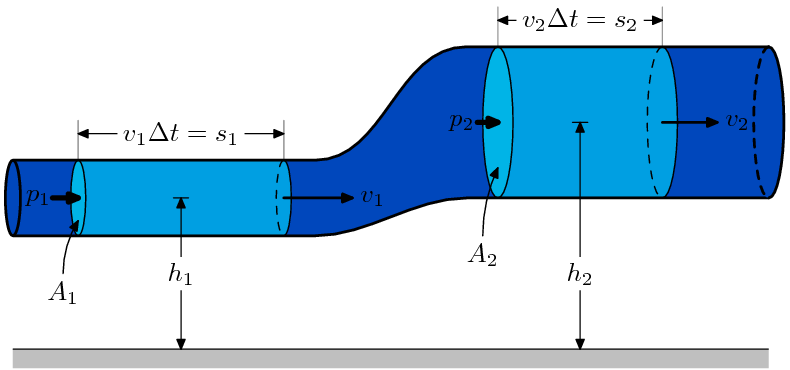
Jeżeli zaniedbać zmianę wysokości odcinków rury to wzór upraszcza się do:

W rurze o mniejszym przekroju ciecz płynie szybciej (v₁ > v₂), w związku z tym panuje w niej mniejsze ciśnienie niż w rurze o większym przekroju.

Ciecz płynąc w rurze o zmieniającym się przekroju ma mniejsze ciśnienie na odcinku,

gdzie przekrój jest mniejszy.

Liczba Reynoldsa - jedna z liczb podobieństwa stosowanych w reologii.

Przy jej pomocy można oszacować stosunek sił bezwładności do sił lepkości.

Liczba Reynoldsa jest kryterium do wyznaczania charakterystyki przepływu

wszelkich płynów nieściśliwych.

Gdzie:

• l - wymiar charakterystyczny

• v - prędkość charakterystyczna płynu

• ρ - gęstość płynu

• μ - lepkość dynamiczna

• ν - lepkość kinematyczna

Liczba Reynoldsa charakteryzuje charakter przepływu. Dla przepływu płynu przez rurę,

gdzie za v przyjmuje się średnią prędkość przepływu, a za l średnicę rury,

zbadano doświadczalnie, że w przybliżeniu dla:

• Re<2300 - przepływ laminarny (uporządkowany)

• 2300<Re<10000 - przepływ przejściowy (częściowo burzliwy)

• Re>10000 - przepływ turbulentny (burzliwy)

Podane granice obszarów są umowne i zależą od cytowanych źródeł. Dla innych przepływów niż w rurach podanie podobnych granic jest również możliwe. Nie istnieją jednak ich uniwersalne wartości, ponieważ zależą od tego co zostanie uznane za "charakterystyczne" w odniesieniu do wielkości v i l (w przypadku płynów ściśliwych także ρ, a dla płynów nienewtonowskich μ).

Liczba ta nazwę swoją wzięła od Osborne'a Reynoldsa - angielskiego inżyniera,

który zaproponował jej stosowanie.

1. Wyznaczenie współczynnika lepkości dynamicznej i kinematycznej cieczy

za pomocą wiskozymetru Hӧpplera.

Opis aparatury:

Urządzenie składa się z cylindra zawierającego szklaną rurkę pomiarową, której oba końce zamknięte są korkami i w której znajduje się ciecz. Całość zamocowana jest w obrotowym statywie, zawierającym zacisk sprężynowy, który służy do unieruchomienia cylindra podczas pomiarów. W rurce znajduje się kulka pomiarowa, której za pomocą stopera, mierzy się czas opadania między dwiema kreskami pomiarowymi zaznaczonymi na rurce.

Rys. 1. Wiskozymetr Hӧpplera

Wykonanie ćwiczenia:

Po odpowiednim ustawieniu urządzenia, obracamy cylinder, aby sprowadzić kulkę

do górnego korka rury pomiarowej, następnie ustawiamy cylinder w pozycji pomiarowej, unieruchamiamy go za pomocą zacisku sprężynowego w dolnej części statywu

i stoperem mierzymy czas opadania kulki między skrajnymi kreskami pomiarowymi.

Pomiary wykonujemy pięciokrotnie.

Uzyskane wyniki pomiarów:

Lp.	τ [s]
1	125,78
2	15,86
3	15,21
4	15,75
5	15,65

Obliczenia:

Dane:

średnica kulki: d = 1,63 cm

masa kulki: G_kulki = 9,6 g

długość odcinka między kreskami: s = 10 cm

masa cylindra: G₁ = 83,85 g

masa cylindra z cieczą: G₂ = 97,11 g

objętość cylindra: V = 14 ml

d = 1,63 cm = 0,0163 m

s = 10 cm = 0,1 m

g ≈ 9,81 m/s²

G_kulki = 9,6 g = 0,0096 kg

r = 0,5·d = 0,5·0,0163 = 0,00815 m

m³

kg/m³

Średni czas opadania kulki:

s

Prędkość opadania kulki:

m/s

G₁ = 83,85 g

G₂ = 97,11 g

V = 14 ml = 0,014 dm³

g/dm³

Współczynnik lepkości dynamicznej:

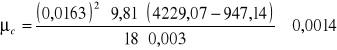
Pa·s

Współczynnik lepkości kinematycznej:

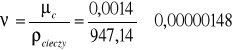
m²/s

Błąd bezwzględny:

s

Błąd względny:

Wnioski:

Błędy wynikające z niedokładnego pomiaru czasu opadania kulki mogły być spowodowane tym, że włączenie i wyłączenie stopera nie nastąpiło równocześnie z momentem przekraczania przez kulkę granicznych kresek.

Możemy również stwierdzić, że prędkość kulki wzrastała z każdym kolejnym pomiarem. Wzrost ten jest spowodowany zwiększeniem się temperatury cząsteczek tworzących ciecz badaną, co z kolei powstaje w wyniku tarcia kulki z cząsteczkami cieczy.

Początkowo cząsteczki badanej cieczy nie tworzyły jednorodnej substancji, w związku z tym kulka na swej drodze napotkała duży opór, dlatego czas jej opadania miedzy kreskami,

tak bardzo się wydłużył. Przy kolejnych pomiarach w jednorodnej już cieczy, opór znacznie się zmniejszył, więc opadanie kulki następowało szybciej.

Błąd ten wynika z niedokładnego oznaczenia gęstości cieczy.

Powstałe błędy mogły również dotyczyć złego ustawienia cylindra (zły kąt),

z niedokładnego wykonywania doświadczenia.

Wyznaczanie gęstości za pomocą areometru.

Opis aparatury:

Areometr to urządzenie służące do mierzenia gęstości cieczy, w którym wykorzystuje się siły wyporu z jaką ciecz działa na zanurzone w niej ciało stałe. Zbudowany jest z pustej szklanej rurki, której górna wydłużona część zaopatrzona jest w specjalną skalę, część dolna w postaci bańki wypełniona jest materiałem o dużej gęstości - śrutem, co pozwala na utrzymanie pozycji pionowej przyrządu zanurzonego w cieczy.

Rys. 2. Klasyczny areometr obciążeniowy.

Wykonanie ćwiczenia:

Począwszy od pierwszego (najmniejszego) areometru kolejno zanurzamy je w badanych cieczach. Głębokość na jaką zanurza się dolna część areometru wynika z różnicy między ciężarem areometru a ciężarem wypartej przez areometr cieczy.

Uzyskane wyniki pomiarów:

Areometr	skala	Gestość [g/cm^3]
				I cieczy	II cieczy
1	0,7 - 0,8	>	>
2	0,8 - 0,9	>	>
3	0,9 - 1,0	>	1
4	1,0 - 1,1	0,098

---