Opracowanie zadań z kolokwium AZ termin 1
Zestaw E :
1a : Nie - granica nie istnieje - podciągi parzyste i nie parzyste zbieżne do -1 i 1
1b : Tak - i w dowolnej potędze to i , -1 , -i lub 1 wiec warunek ten jest spełniony
1c : Tak - ten zbiór sprowadza się do nierówności x2/3=<y2 co wyglada jak spłaszczony do 2 wymiarów stożek
co jest zbiorem domkniętym bo zawiera brzeg i nieograniczony w sposób widoczny.
2a Nie : aby spełniona była równość część urojona sin z musi się zerować (Im z : C -> R), a łatwo rozpisując sin z stwierdzić że się nie zeruje przecież wszędzie
2b Tak : ![]()
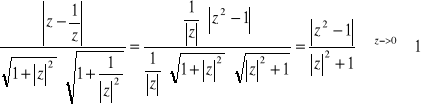
2c Tak :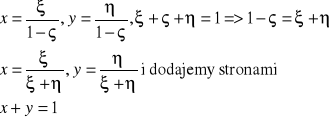
3a Tak : zamiast górnego wzoru można pomnożyć licznik i mianownik przez z i mieć ![]()
, 3 potęga górną pół oś urojoną przeprowadza na dolną , a dolną na górną. Moduł w mianowniku zmienia tylko odległość od punktu (0,0)
3b Nie - na ta chwilę .... trzeba sprawdzić warunki CR i ciągłość w otoczeniu 0 . Nam wyszło że CR nie jest spełnione zatem obstawiam że nie. Mogę się mylić
3c Nie - wykonać wykres (wygląda jak sinus) skoro nie ma przecięć wykresu ze sobą to funkcja jest różnowartościowa więc jest łukiem zwykłym. Ale przyjmuje wartość równą 0 dla t =0 więc nie jest gładki
4a Nie - liczymy promień zbieżności wychodzi 1/3 więc w promieniu 2 nie jest BZW
4b: Tak - ale bez sensownego komentarza
4c Nie : weźmy dwa szeregi o ciągach współczynnikow
ck = 1 dla parzystych i ck=0 dla nieparzystych
dk = 0 dla parzystych i dk=1 dla nieparzystych.
Założenia spełnione a szereg wynikowy to szereg zer o R=+oo
5a tak : intuicyjnie rysujemy kółka dla coraz większych R aż w końcu okrąg się rozprostuje. Symetria wobec prostej oznacza teraz symetrie wobec osi rzeczywistych.
5b Nie - hmm sporne czy z=oo należy do dziedziny funkcji zespolonej ? wg mnie i wykładu - nie więc Nie .
5c Tak - odsyłam do pliku image09036 z zeszłorocznego koła
6a : punkt z0 z wzoru Cauchy'ego równy tu 0 nie należy do wnętrza koła C(2,1) zatem całka równa 0
6b Nie : parametryzujemy krzywą 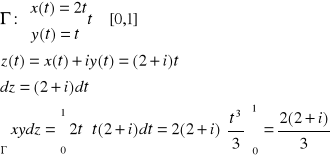
6c Tak : obrazem h (D) jest pas od -1/4 i do -1/2 i . Jest on węższy niż 2Pi stąd funkcja exp (normalnie 2kPi * i okresowa) jest różnowartościowa.
Zestaw F:
1a : Nie - dla liczb o dużym module odległość jest ujemna <- bzdura
1b Tak : zauważyć (najlepiej na boku), że ![]()
rozpisać tg na sin / cos .
sin i cos na ich postać zespoloną. Potem to samo z drugiej strony i wychodzi to samo
1c Tak granica z prawej strony !! NIE ISTNIEJE !! dla x -> oo przez ujemne exp(x)->0
dla x->oo przez dodatnie exp(x)->+oo. Granica z lewej strony istnieje
2a Nie : 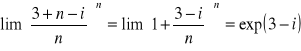
wtedy lewa strona to liczba postaci
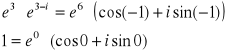
więc są to liczby o różnych modułach ... zatem są różne
2b Tak : !!SUMA WSZYSTKICH PIERWIASTKÓW LICZBY ZESPOLONEJ DOWOLNEGO STOPNIA n>1 JEST RÓWNA 0!! Prosta własność sumy wektorowej
2c Nie : rozwiązaniem zbioru jest część płaszczyzny o warunku 1 < (x-1)^2+y^2 , zewnętrze koła zeC (a oo nie należy) więc brzeg jest niespójny zatem jest niejednospójna (inaczej łuk zamknięty oplatający to koło jest nieściągalny w tej płaszczyźnie)
3a Nie : f nie jest ciągła po osi OX, więc nie istnieje pochodna cząstkowa po x wiec nie ma pochodnej zespolonej
3b Nie : na osi OX\{0} jest stała =1 na całej urojonej = 0 ... jasne że róznowartościowa :P
3c Nie : obraz osi urojonej = {0} obraz osi rzeczywistej {0,1} ... który w którym się zawiera ?
4a Tak : E = to koło bez środka ... coś takiego jest spójne więc zachodzi twierdzenie o jednoznaczności gałęzi logarytmu (treść jak w zadaniu)
4b : lewa strona to exp(ia(z)), logarytmujemy(po zespolonemu) stronami i otrzymujemy że a(x)=Arg Z + 2kPi
4c Nie : weźmy dwa szeregi o ciągach współczynników
ck = 1 dla parzystych i ck=0 dla nieparzystych
dk = 0 dla parzystych i dk=1 dla nieparzystych.
Założenia spełnione a szereg wynikowy to szereg zer o R=+oo
5a nie : część rzeczywista szeregu jest rozbieżna. Ma minorantę cos(Pi/3) / n rozbieżną. Zatem szereg zespolony jest rozbieżny
5b Nie : Koła zbieżności to D(1,1) i D(0,1) i nie są rozłączne
5c Nie : brak punktów istotnie osobliwych . Dla x=kPI /=0 bieguny, dla x=0 pozornie
6a: Nie : f regularna tzn ciagła w sensie R^2. Z analizy 2, dla funkcji ciągłych postać pochodnych cząstkowych mieszanych nie zależy od kolejności różniczkowania stąd to róznica jest równa 0
6b Nie: Standardowe zadanie na residua. Dwa bieguny krotności 1 i jeden punkt pozorny. Residua w biegunach równe `-i' i `i' stąd suma residuów = 0
6c Nie : Jeżeli część o RE >0 jest wnętrzem koła a część o RE < 0 zewnętrzem to oś OY jest osią symetrii dla punktu 0 i oo . Jak widać jednak tej symetrii być nie może. Stąd nie ma takiej homografii.
Wyszukiwarka