Opracowanie: Piotr Pietruszka

WYKŁAD 21

,
(*)

,

,

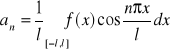
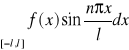
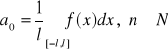
WNIOSEK:

Szereg (*) jest zbieżny przeciętnie z kwadratem do f w [-l,l]

(zbieżność w sensie
)

Tzn.

ciąg sum częściowych szeregu Fouriera (*)

DEFINICJA 21.1

Niech f - ograniczona w [a,b]

1. f - przedziałami monotoniczna
   jeżeli [a,b] da się podzielić na skończoną ilość podprzedziałów, w których funkcja jest monotoniczna.

2.
- punkt nieciągłości pierwszego rodzaju

PRZYKŁAD 21.1

nie jest przedziałami monotoniczna w [0,1]

DEFINICJA 21.2 (WARUNKI DIRICHLETA)

funkcja w [a,b] spełnia warunki Dirichleta

1. Jest przedziałami monotoniczna w [a,b]

2. posiada co najwyżej skończoną ilość punktów nieciągłości I rodzaju i: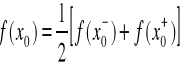
   

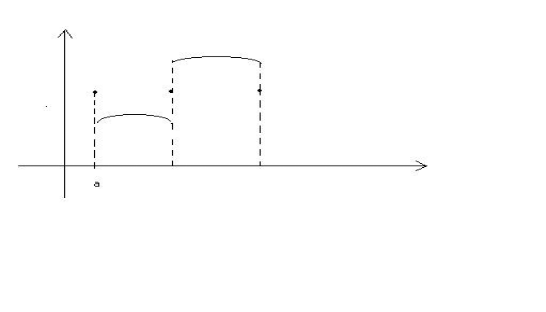
3. 
   

TWIERDZENIE 21.1 (DIRICHLETA)

Z:

f - spełnia warunki Dirichleta w [-l,l]

T:

PRZYKŁAD 21.2

Niech

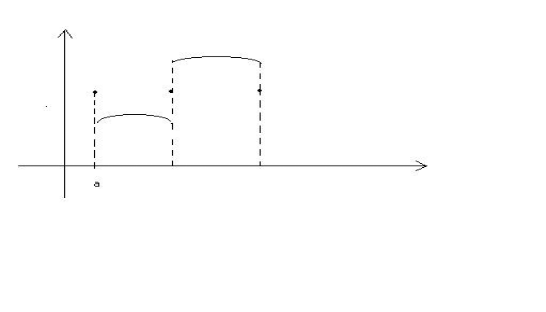
Rozwinąć f(x) w szereg Fouriera, narysować wykres sumy i obliczyć wartość sumy w punkcie

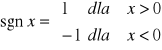
f- nieparzyste

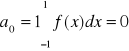
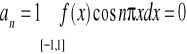
nieparzysta parzysta

nieparzysta

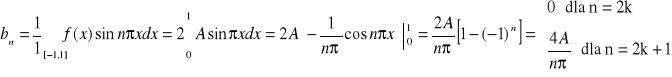
UWAGA 21.1

=

Suma szeregu Fouriera jest f. okresową o okresie zasadniczym 2l.

UWAGA 21.2

1. Jeżeli f - nieparzysta , to

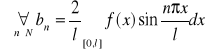
- szereg sinusów

2. Jeżeli f- parzysta , to
   
   

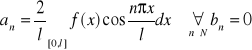
szereg cosinusów

NIEPEŁNE SZEREGI FOURIERA

Niech

1. Rozwinąć f w szereg sinusów w [0,l]

2. Rozwinąć f w szereg cosinusów w [0,l]

3. Rozwinąć f w pełny szereg Fouriera w [0,l]

Ad 1

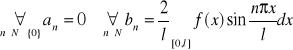
Ad 2

UWAGA 21.3

Jeżeli f jest okresowa o okresie zasadniczym T

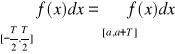
ZAGADNIENIE:

Rozwinąć f w szereg Fouriera w przedziale [a,b] ,

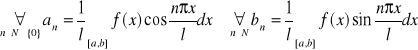
Ad 3. Rozwinąć f w szereg Fouriera w [0,l]

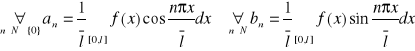
PRZYPOMNIENIE:

Postać zespolona szeregu Fouriera

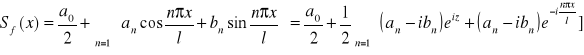
zauważmy, że:

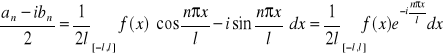
oraz

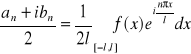
Niech

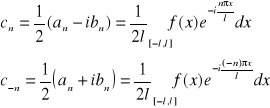
wobec tego

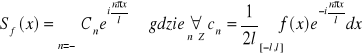
DEFINICJA 21.3 (WIDMO AMPLITUDOWE)

Jeżeli

Ciąg
- widmo amplitudowe funkcji

DEFINICJA 21.4 (WIDMO FAZOWE)

arg
jeżeli

0 jeżeli
- widmo fazowe funkcji

jeżeli