Podstawy techniki systemów

wg dr inż. Andrzeja Żołnierka

Literatura: „Podstawy informacji zarządzania” Budnicki J.

WYKŁAD I

TEORIA I TECHNIKA SYSTEMÓW

1. Tworzenie modeli i modelowanie.

2. Identyfikacja i rozpoznawanie.

3. Analiza i projektowanie.

4. Sterowanie i kierowanie.

Ad1. Tworzenie Modeli i modelowanie.

Badamy system po to, żeby na niego oddziaływać. Musimy stworzyć opis/model takiego urządzenia, aby z niego korzystać.

Modelowanie: Przebadać model empirycznie, jak coś nie gra zmienić program, uprościć, skomplikować model. Im więcej powiązań z otoczeniem, z jakim dany obiekt funkcjonuje, tym bardziej skomplikowany (skomplikowane algorytmy itp.).

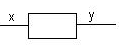
Tworzenie modeli:

I Przykład(hipotetyczny.)

x- ilość produkcji y- koszt

y = F(x) - model tego systemu (ekonomicznego)

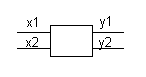
II Przykład: y1 = F(x1,x2)

2 wierze destylacyjne, y2 = F(x1,x2)

które mogą robić Podanie takiej

to samo zależności WE/WY

tj. podanie modelu

y₁=a₁₁x₁ + a₁₂x₂

y₂=a₁₁x₁ + a₂₂x₂

Czy jest to model dobry?

Nie wiem, będę musiał sprawdzić: weryfikacje, modulacje.

Ale uznaje, że ten model jest dobry. Jest to model liniowy. Jest to macierz kwadratowa, lub prostokątna w zależności od ilości WE i WY.

Model Statyczny - nie występuje czas, interesuje mnie obserwacja w danym momencie, jak stany znikną podczas badania, to efekt nas interesuje.

Y=Ax

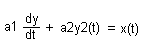
Model dynamiczny - występuje czas, stan aktualny zależy od stanów poprzednich.(np. wzrost produkcji i dynamika wzrostu)

a1,a2 > 0

Przykład : Model matematyczny opisujący prąd przemienny.

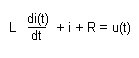
Do opisów modeli dynamicznych zawsze będzie potrzebne równanie różniczkowe

WYKŁAD II

IDENTYFIKACJA, ROZPOZNAWANIE

(b. Specyficzna identyfikacja)

y₁ = a₁₁x₁ + a₁₂x₂

y2 = a₂₁x₁ + a₂₂x₂

Mamy nieznane parametry:

a₁₁=? a₁₂=? a₂₁=? a₂₂=?

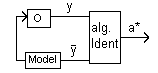
Algorytm identyfikacji - sposób na wyznaczenie tych parametrów.

Eksperyment:

BIERNY	AKTYWNY
W układzie krwionośnym nie można np. podwyższyć ciśnienia u pacjenta, bo umrze, Można u pacjenta zaobserwować ciśnienie np. dziś i jutro, mam 2 wyniki i je przetwarzam.	Jeżeli sami możemy ustalić, zaplanować wejścia. Wykonuje doświadczenie. Np. Sam ustawiam WE.

Identyfikacje przeprowadzamy w przypadku, kiedy znamy dokładny model systemu.

Przykład:

y₁ = a₁₁x₁ + a₂₁x₂ X_1,X₂ - ilość surowców przerabianych w 2 agregatach

y₂ = a₂₁x₁ + a₂₂x₂ Y₁,Y₂ - ilość produktu i kosztu produkcji

Y = AX

A = YX^-1 - algorytm identyfikacji

A = Ψ (x₁,x₂,y₁,y₂)

_

y = Ø (x, a) zakładam sobie model z dokładnością parametrów

Ilość obserwacji WY zew. obiektu

↓ ↓

_{n _ n}

Q_I =∑ ( y_i - y_i )² =(mają nie być różne od siebie)= ∑ ( y_{i -} Ø(a₁ x_i ))²

^{i=1 i=1}

^↑

^{WY modelu (wylicze sobie)}

Min Q(a) → a*

^a

Obliczam I pochodną i sprawdzam I lub II warunek wystarczający istnienia min funkcji.

_{_}

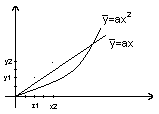
y = ax

_{_}

y = ax² - klasa modeli kwadratowa Obliczanie sumy

odl. od prostej

pomiary i-tego a

_{n n}

Q_I = ∑ (y₁ - Ø(a₁x_i))² = ∑ (y₁ - ax₁)²

^{i=1 i=1}

_{dQ n}

― = ∑ 2(y₁ - ax₁) (-x_i) = 0

^{da i=1}

_n

∑ (ax_i² - x_iy_i) = 0

ⁱ⁼¹

_{n n}

a ∑ x_i² - ∑ x_iy_i = 0

^{i=1 i=1}

_n

∑ x_iy_i Algorytm identyfikacji wygląda dokładnie tak.

ⁱ⁼¹ Model statyczny, liniowy.

a = ------------- Najlepsze rozwiązanie w miare minimalizacji danego kryterium

_n

∑ x_i²

ⁱ⁼¹

ANALIZA

Analiza (Systemu) ilościowa:

Pytanie: Jak zachowuje się WE, kiedy zmieni się WE?

Dokonuje analizy działania systemu. Jak zachowuje się WY dla różnych WE, tj. zadanie ANALIZY.

W przypadku prostych układów wyliczenie y znając konkretne wartości parametrów.

DEF.

„Jeżeli znamy wartości liczb parametrów a₁₁,a₁₂,a₂₁,a₂₂ to wstawiamy dane x₁,x₂ do modelu i wyliczamy y₁,y₂.”

Analiza jakościowa:

Czy system ma pewne własności np. czy jest stabilny(pewne wielkości nie będą dążyć do nieskończoności).

PROJEKTOWANIE

Projektowanie - Podejmowanie decyzji

Czy mogę ustawić y i dobrać x, żeby y były takie jak ja sobie życzę ?

Zaprogramować system - przewidzieć co dać na WE aby WY osiągnęło taki stan jak ja sobie życzę.

DEF.

„Dla danych wartości a oraz zadanych wartości y₁=y₁* , y₂=y₂* można wyliczyć decyzje x₁,x₂”

y₁*=a₁₁x₁+a₁₂x₂ Musze rozwiązać ten układ względem tych 2 niewiadomych, I wtedy y

y₂*=a₂₁x1+a₂₂x₂ osiągnie na pewno stan taki jak chce.

y₁*a₂₂ - y₂*a₂₁ y₂*a₁₁ - y₁*a₂₁

x₁ = x₂ =

a₁₁a₂₂ - a₂₁a₁₂ a₁₁a₂₂ - a₂₁a₁₂

STEROWANIE/KIEROWANIE

Co by się stało, gdyby y₁ i y₂ zmieniło się?

Codziennie ustala się np. rozmiar produkcji i koszty) codziennie się zmieniają i wtedy musze przetestować „system”, musze nim kierować.

DEF.

Reakcja na zmieniające się parametry - kierowanie/sterowanie

**Pyt. Kolokwialne:

Wyjaśnij zadanie projektowania a zadanie sterowania na prostym przykładzie.

ETAPY MODELOWANIA MATEMATYCZNEGO

1.Sformułowanie celów modelowania.

2.Wybór kategorii modelu i określenie jego struktury.

3.Identyfikacja.

4.Algorytmizacja obliczeń.

5.Weryfikacja.

SFORMUŁOWANIE CELÓW

Pytanie po co to robię? Co chce zbadać, wykryć? Do czego będzie mi to służyć?

1.Opis i wyjaśnienie działania mechanizmu systemu - model FENOMELOGICZNY

2.Przewidywanie zachowania systemu w przyszłości i przy różnych warunkach, oddziaływanie na system - model PROGNOSTYCZNY.

3.Wybór właściwych oddziaływań WE spełniających określone warunki - model DECYZYJNY.

4.Wybór struktur, lub parametrów spełniającego określone zadania - model NORMATYWNY.

WYBÓR KATEGORII MODELU I OKREŚLENIE JEGO STRUKTURY

Zależy od natury modelu: statyczny, dynamiczny...

Każdy system, obiekt jest powiązany z otoczeniem. Dlatego trzeba uwzględnić wpływ otoczenia. Trzeba pójść na ustępstwa: np. nie bierzemy pod uwagę pogody. Im więcej pominiemy, tym model będzie prostszy, ale nie może być za prosty.

Trzeba osiągnąć kompromis pomiędzy: komplikacją modelu, a zbytnim upraszczaniem.

IDENTYFIKACJA

Model zbyt skomplikowany, jest złym rozwiązaniem. Może być bardzo dokładny, ale przez tą dokładność mam zbyt mało danych pomiarowych, pomiarowych model ten jest niemożliwy do skonstruowania, więc wracam się i upraszczam go.

ALGORYTMIZACJA OBLICZEŃ

W końcu muszę cos obliczyć.

Np. Więcej niewiadomych niż równań (nieskończenie wiele rozwiązań).

Jak przystępuje do obliczeń może wystąpić kilka różnych rozwiązań:

1.Nieskończenie wiele rozwiązań : Źle

2.Sprzeczny(wróć i wykryj błąd) : Źle

3.Jedno rozwiązanie : Dobrze

WERYFIKACJA

Czy da się policzyć?

Czy mam określony rodzaj zgodności?

Czy wyniki doświadczalne zgadzają się z wynikami rzeczywistymi?

Itp....

Jeżeli któryś z warunków się nie zgadza to wracam do poprzednich etapów

DEF.

„Jest to porównanie wyników modelowania z zachowaniem się systemu

rzeczywistego.”

Kryteria Wewnętrzne:

- Zgodność FORMALNA - czy jest to układ zdań poprawnych i spójnych

- Zgodność ALGORYTMICZNA - Jak są np. 2 rozwiązania, to trzeba w razie potrzeby mieć zaszyte mechanizmy, które pozwolą wybrać jedno z możliwych rozwiązań.

Kryteria Zewnętrzne:

- Zgodność HEURYSTYCZNA - czy zbudowany model ma walory interpretacyjne/naukowe, że wyjaśnia działanie systemu. Nabieranie wiedzy o systemie. Model oddaje, interpretuje mechanizmy, które w nim zachodzą.

- Zgodność PRAGMATYCZNA

- Zgodność REPLIKATYWNA - Jeżeli zbudowany model obiektu ma podstawy obiektu, to ten model będzie działał podobnie jak system na podobnych warunkach.

- Zgodność PREDYKATYWNA - Aby model dobrze działał , jak pojawią się dane, których nie było podczas sprawdzania (np. w modelach ekonomicznych). Gdybanie, Przewidywanie.

- Zgodność STRUKTURALNA - Aby model dokładnie oddawał mechanizmy, które rządzą tym modelem, obiektem.

TERAZ MOŻNA ZAPEWNIĆ SYMULACJE KOMPUTEROWE, KIEDYŚ WSZYSTKO NA PIECHOTE, B.ŻMUDNE OBLICZENIA.

KONIEC INFORMACJI OGÓLNYCH

POJĘCIE SYSTEMU

1.Idea wyodrębniania systemu z otoczenia.

2.Idea budowy systemu z elementów(Podsystemy).

3.Idea funkcji spełnianej przez system.

4.Idea ograniczonej zmienności systemu.

Ad 1.

System jest pewną całością, w której współdziałają wyodrębnione części składowe. Funkcjonowanie systemu zależy od funkcji części składowych, i związków między nimi, powiązania części składowych określają strukturę systemu.

Np. samochód jest systemem.

Ad.2-3.

System jest pewną całością i spełnia wspólny jakiś określony cel.

Ad.4.

Formuły matematyczne jakie przyporządkujemy dla systemu, tylko przez jakis czas będą aktualne.

WYKŁAD III

ETAPY PROJEKTOWANIA SYSTEMU STEROWANIA

1.Analiza systemu O.S.(modelowanie).

2.Identyfikacja O.S.

3.Opracowanie algorytmu sterowania.

4.Opracowanie komputerowego programu sterującego.

5.Opracowanie systemu realizującego program sterujący.

Analiza systemu ma uzmysłowić, że mamy działać celowo. Sprecyzować problem, zrobić tak,

Aby wszystko działało, a następnie stworzyć.

Modelem matematycznym systemu(obiektu, procesu) jest zestaw wzorów matematycznych. Ogólnie zestaw relacji matematyczno-logicznych, określających zależności pomiędzy wyróżnianymi wielkościami, są to wielkości WE/WY systemu, a system taki nazywany względnie odosobniony. W pojęciach WE i WY zawarte jest domniemanie o związku przyczynowo-skutkowym, między tymi wielkościami. wielkościami tym sensie, że obserwując WE można określić WY. Zdarzenia nie są losowe, tylko zaplanowane.

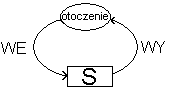
System wyodrębniony z otoczenia:

Otoczenie oddziałowywuje, na system, poprzez WE( przykład

takiego systemu- auto: WE- naciskanie

gazu, a WY tj, prędkość)

DYNAMIKA SYSTEMÓW

Własności dynamiczne systemu wynikają z działania następujących ogólnych zasad fizycznych:

- przy ograniczonych wydajnościach źródeł, każda nieskończenie mała zmiana stanu energetycznego, lub materiałowego wymaga pewnego czasu( bezwładność inercja).

- każde skończone przemieszczanie się w przestrzeni zjawiska materialnego wymaga pewnego czasu - opóźnienie.

DYNAMIKA - (nie szybkość, nie działalność niezrównoważonych sił) Stan obiektu/systemu, nie zależy, od tego, co jest na WE w danym momencie, tylko od historii.

//*Przykład I: Ilość biomasy marchewki, uzależnione jest od słońca i deszczu, czy jest duża zależy od historii, a nie od tego, czy w momencie badania świeci słońce, czy nie.//

//*Przykład II: Odpalenie Windowa, stan komputera, aby wykonywała się dana funkcja windowa, np. logowanie, musi nastąpić szereg instrukcji poprzedzających, bez których nie dojdzie do logowania//

//*Przykład III: charakter narastania temperatury w czasie(PIEC). Im dajemy wyższe napięcie, tym piec się szybciej nagrzewa, ale i tak jakiś czas to trwa. Czas nagrzania nie może być = 0

Zjawiska dynamiczne:

- charakter bezwładny( uczenie się matematyki: 1 impuls(„ucz się”), bezwładność, opóźnienie, potem 2 impuls(„dostajesz pałke”), zaczyna trybić).

- opóźnienia: Jazda autem, zauważam przeszkodę, nie staje od razu, tylko zajmie to trochę czasu: czas reakcji, wytracenie energii. Cały proces jest opóźniony.

DEF.

Miejsce, gdzie inst.. WE i miejsce WY są rozłożone w czasie.

Pokonanie przestrzeni czasu zawsze wymaga jakiegoś czasu.

Matematycznie - różne stany przejściowe, lub stany nieustalone

PIEC

Są to tzw. Przebiegi przejściowe

Tutaj już mniejsza bezwładność (to już nie pasuje do pieca)

Układ będzie dążył do jakiegoś układu ustabilizowanego, lub nie

Magistrala - układ dynamiczny(generator) o stabilnej częstotliwości

DEF.

Precyzyjna definicja matematyczna związana z dynamiką:

Rys wyjaśnienie:

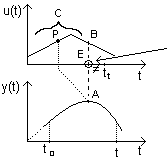
Historia WE ma wpływ do tego momentu, ale bez tego punktu,

Czyli C ma wpływ bez E.

Wartość WE w B nie ma wpływu na wart WY w A (ukł. Dynamiczny), ale na wart. WY ma wpływ cała Historia - C, lub

Tylko punk w Historii - P.

To że czas występuje w danym systemie, nie oznacza że układ jest układem dynamicznym, natomiast kiedy czas nie występuje to na pewno układ NIE jest dynamiczny.

Stan systemu dynamicznego :

Jest to najmniejsza liczba danych(wektor stanu), których znajomość danej chwili, przy znajomości wielkości WE, począwszy od tej chwili pozwala jednoznacznie określić stan i wielkości WY systemu w przyszłości.

Zdeterminowanie systemu wynika z postulatów: przyczynowości, zupełności.

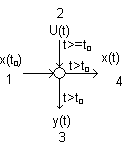
Ilość zmiennych stałych, które określają położenie danego

Obiektu jest różna.

1 i 2 wpływa na 3 i 4

Więc systemy są zdeterminowane, znając stan WE można

Obliczyć WY.

Postulat przyczynowości:

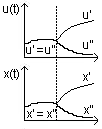
Not: Dopóki WE stanu jest takie same, to sterowanie tez takie

same => przyczyna zmiany stanu.

Postulat zupełności:

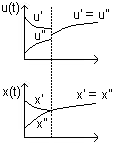
Not: Zmian jest jednoznaczna w odwrotną stronę. Kiedy WE stanu jest takie same, to sterowanie różne, natomiast jak sterowanie takie same, to WE stanu też

Przykład:

Zbiornik wody - stopień zapełnienia:

Dx(t)

------ = u(t) - y(t)

dt

↑ ↑ ↑

WE WY

prędkość zmiany co wpływa do to co wypłynęło, już

stanu(pochodna) wykonania wypływa

(tutaj woda,

deszcz)

y(y) = y(x(t))

wyznaczam x(t):

_{t t}

x(t) = ∫ u(t)dt - ∫ y(t)dt

• ⁰

Całka oznaczona - suma wielkości, sumowanie przebiegu, który zmienia się w czasie

Całka - sumowanie, czyli uwzględnienie tego , co było po drodze.

WYKŁAD IV

METODY OPISU CIĄGŁYCH LINIOWYCH JEDNOMIAROWYCH OBIEKTÓW STEROWANIA

1. Równania różniczkowe opisujące jednowymiarowe obiekty sterowania ( w szczególności WE-WY).

2. Odpowiedź jednostkowa (skokowa).

3. Odpowiedź impulsowa.

4. Transmitacja operatorowa.

5. Transmitacja widmowa.

6. Metoda przestrzeni fazowej i płaszczyzny fazowej.

7. Metoda zmiennych stanu.

8. Charakterystyki częstotliwościowe.

2.Przedstawia jak zachowuje się obiekt kiedy na WE pojawia się sygnał skoku (wymuszenie).

3.Odpowiedź obiektu na krótkotrwały impuls(np. doprowadzam auto do jakiejś prędkości, przychodzi podmuch wiatru i wytrąca, muszę ulepszyć, zaplanować sterowanie.

4.Transformata Laplace'a.

5-6-7-8.Bardzo złożone.

Dlatego tak dużo opisów, bo różnie są wygodne w różnych analizach.

Matematyczna zmiana stanu - wiemy nie tylko co dzieje się na zewnątrz, ale także wewnątrz.

Charakterystyką(Odpowiedzią) skokową:

H(t) jednowymiarowego układu (obiektu) liniowego stacjonarnego, nazywać będziemy odpowiedź tego układu na wymuszenie w postaci jednostkowej funkcji skokowej 1(t), przy zerowych warunkach początkowych.

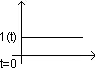
←impuls

Charakterystyką( Odpowiedzią) Impulsową

G(t)liniowym układu( Obiektu) liniowego, stacjonarnego nazywać będziemy odpowiedź tego układu na wymuszenie w postaci funkcji Diraca (t), przy zerowych warunkach początkowych.

δ(t) ←impuls o nieskończonej amplitudzie, duży impuls,

o dużym czasie trwania.

Transmisją operatorową:

G(s) liniowym układu (Obiektu) liniowego stacjonarnego nazywać będziemy wartość określoną jako stosunek transformaty wymuszenia U(s) tego układu przy zerowych warunkach początkowych. G(s) =Y(s) / U(s)

TYPOWE CZŁONY LINIOWE

- Człon proporcjonalny

- Człon inercyjny I rzędu

- Człon całkujący idealny( na WY jest całka)

- Człon całkujący z inercją( to samo, tylko zaburzone)

- Człon różniczkujący( na WY pochodna sygnału WE)

- Człon różniczkujący z inercją( to samo ale zaburzony)

- Człon oscylacyjny( złożenie członów inercyjnych inercyjnych rzędu)

- Człon oscylacyjny II rzędu

- Człon opóźniający( to co na WE opóźnione na WY)

CZŁON BEZINERCYJNY

( proporcjonalny wzmacniający)

Równanie różniczkowe WE/WY: y= ku

k - współczynnik wzmocnienia określony jako stosunek odpowiedzi y do wymuszenia w stanie ustalonym.

T - stała czasowa = 0

Charakterystyka skokowa: g(t) t

h(t) = k1(t)

Charakterystyka impulsowa: h(t)

h(t) = k δ(t) t

Transmitacja:

Gi(s) = k

Kierunek przepływu prądu

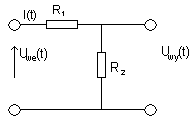
**Przykład 1: Wybieram wielkości WE i WY CZWÓRNIK czwórnika, zakładam jeszcze, że (Dzielnik jest nieobciążony.

Napięcia)

I(t) - prąd płynie, wiedzieć to musze, aby znać zależności między U_we(t) i U_wy(t).

U_we(t) = I(t) * (R₁ + R₂)

U_wy(t) = I(t) * R₂ => I(t) = ....... wyliczam I(t) i podstawiam

R₁ + R₂

U_we(t) = U_wy(t) Schemat postępowania: Wypisywanie równań opisuje

R₂ opisuje zachowanie się układu.

R₂

U_wy(t) = U_we(t)

R₁ + R₂

**Przykład 2:

PRĄDNICA TACHOMETRYCZNA PRĄDU STAŁEGO

(Jazda autem prędkościomierz przekłada prędkość obrotu kół na napiecie i pokazuje na prędkościomierzu).

Tu przychodzi strumień

Wzbudzenia(prądnica)

Nieobciążona, poruszam się w liniowym zakresie magnesowania

E(t) = U(t)

E(t) = C_E Ø Ω(t)

U(t) = C_E Ø Ω(t)

y(t) = k * U(t)

Najprostrzy człon proporcjonalny, bezinercyjny

CZŁON INERCYJNY:

(piec)

(Jak funkcja określona w czasie

I - pochodna mówi o prędkości zmian

II - pochodna o przyspieszeniu)

.

Równanie różniczkowe WE/WY: Ty + y = ku

k - współczynnik wzmocnienia określany jako stosunek odpowiedzi y do wymuszenia u w stanie ustalonym.

T - stała czasowa.

Charakterystyka skokowa:

h(t) = k( 1 - ex [(-1)/T]) 1(t)

Odpowiedź impulsowa:

g(t) = K/T ex [(-1)/T] 1(t)

Transmitacja:

k

G_s =

1 + sT

kierunek przepływu prądu

**Przykład 1:

CZWÓRNIK RC

Nieobciążony.

U_we(t) = RI(t) + 1/C ∫ I(t) dt

U_we(t) = RI(t) + U_wy(t)

U_wy(t) = 1/C ∫ I(t) dt

d U_wy(t) 1

= * I(t) tj. funkcja czasu

dt C

RC d U_wy

U_we(t) = . * + U_wy

T y + y dt

Oznacza to, że jak włącze napięcie na WY nie pojawi się niezwłocznie, tylko będzie narastać.

Im stała czasowa mniejsza, tym szybciej zostanie osiągnięty stan przez WY.

**Przykład 2:

ELEMENT GRZEWCZY:

P - moc jest funkcją czasu P(t); energia dostarczana do grzejnika

dt - mały czas (delta t) energia ta rozkłada się na ciepło

dodawane i wydalane

P(t)dt = c*m *d Θ(t) + α
S Θ dt α - stała

S - powierzchnia grzejnika

Θ - ilość ciepła proporcjonalna do

To co się kumuluje to co się rozprasza temp, zmienia się w czasie

w grzejniku

Mamy bilans cieplny:

P(t)dt = c*m*d Θ(t) + αS*Θ(t) dt

1 c*m d*Θ(t) .

* P(t) = * + Θ(t) k*u(t) = T * y + y

α*S α * S dt

**Przykład 3:

GENERATOR

PRĄDU STAŁEGO

Nieobciążony

I_u(t) - prąd wzbudzenia

d*I*w(t)

L + R*I*w(t) = Uw(t)

dt

d*E(t) d*I(t)

= K

dt dt

L d*e(t) R

* + E(t) = Uw(t)

K dt K

Podsumowanie:

Co uzyskujemy?

Układy o różnych naturach podlegają pod te same równania jak odrzuce skale i jednostkę MATEMATYKA jest wszędzie.

Wykład V

CZŁON RÓŻNICZKUJĄCY

.

Równanie różniczkujące WE/WY: y = ku

K - współczynnik wzmocnienia określony jako stosunek odpowiedzi y do pochodnej wymuszenia w stanie ustalonym

T - stała czasowa = 0

Charakterystyka skokowa: h(t) = uδ(t)

dδ(t)

Odpowiedź impulsowa: g(t) = k (pochodna z odpowiedzi skokowej)

dt

Transmitacja: g(s) = ks

Przykład:

(nie ma idealnych członów różniczkujących)

dU(t)

KONDENSATOR i(t) = c

dt

Uc(t) = 1/c ∫ i(t) dt

CZŁON RÓŻNICZKUJĄCY Z INERCJĄ

(rzeczywisty człon różniczkujący)

. .

Równanie różniczkujące WE-WY: Ty + y = ku

K - współczynnik wzmocnienia określany jako odpowiedź y do pochodnej wymuszenia u w stanie ustalonym

T - stała czasowa

k 1

Charakterystyka skokowa: h(t)= exp ( - ) 1(t)

T T

Odpowiedź impulsowa: k k 1

g(t)= δ(t) - exp( - ) 1(t)

T T² T

ks

Transmitacja: g(s) =

1+sT

Przykład:

CZWÓRNIK R,L d I(t)

U_we(t) = R * I(t) + L =

dt

= R I(t) + U_wy(t)

dI(t)

U_wy(t) = L

dt

d U_we(t) d I(t) d U_wy(t)

= R +

dt dt dt

Równanie końcowe:

d U_we R d U_wy . _.

= * U_wy(t) + => u = k * y + y

dt L dt

Przykład **:

TRANSFORMATOR :

d I₁

U₁ = RI₁ + L₁

dt .

I

d I₁

U₂ = M

dt

. . ..

U₁ = R₁ I₁ + L₁ I

. R L₁ .

U₁ = U₂ + U₂ / M/R

M M

M . L₁ .

U₁ = U₂ + U₂

R R₁

K T

CZŁON CAŁKUJĄCY IDEALNY

(wykonuje operację odwrotną) :

.

Równanie różniczkowe WE - WY: y = ku

K - współczynnik wzmocnienia prędkościowego, określany jako stosunek pochodnej odpowiedzi y do wymuszenia u w czasie ustalonym.

Charakterystyka skokowa (stała): h(t) = k t 1(t)

Odpowiedź impulsowa (pochodna): g(t) = k 1(t)

K

Transmitacja: g(`s) =

S'

Przykłady:

ZBIORNIK Z CIECZĄ

We - objętość cieczy dopływająca jednostce czasu ( g(t) )

Wy - poziom cieczy

G(t) d V(t)

G(t) =

dt

str. dopływający Szybkość narastania

objętości

wys. Słupa wody: h(t) * S = V(t)

d h(t)

S = g(t)

dt

_t

h(t) = 1/s ∫ g(t) dt

⁰

2. Kondensator idealny.

3. Układ napędowy pozycyjny.

CZŁON CAŁKUJĄCY Z INRCJĄ

.. .

Równanie różniczkowe WE - WY: Ty + y = ku

K - współczynnik wzmocnienia prędkościowego określany jako stosunek pochodnej odpowiedzi y do wymuszenia u w stanie ustalonym

T - stała czasowa

Charakterystyka skokowa:

t

h(t) = (kt - kT ( 1-exp [- ] ) ) 1(t) układ będzie dążył do całki

idealnej.

T

Odpowiedź impulsowa:

t

h(t) = k [ 1-exp [- ] ] 1(t)

T

K

Transmitacja: g(s) =

S(1+sT)

Przykłady:

1. OBCOWZBUDNY SILNIK PRĄDU STAŁEGO

Założenia: silnik nieobciążony, uwzględniamy tylko bezwładność

We - napięcie twornika

Wy - kąt położenia wału silnika

Ω(t) (WY - położenie kątowe)

α(t)

Ø - strumień jednego z uzwojeń

Const

DI(t)

U(t) = R_t * I(t) + L_t E(t)

dt

pomijam(małe)

dΩ(t)

M_n(t) - M_z(t) = I M_n(t) = C_m * Ø * I(t)

dt

Chcemy powiązać 2 wielkości: α(t) i U(t)

d α(t)

= Ω(t) No i manipulujemy, aby była zależność α(t) do U(t)

dt

dΩ(t)

C_m Ø Ω(t) * I(t) = J

dt

U(t) = R_t * I(t) + C_E Ø Ω(t)

J dΩ(t)

I(t) = *

C_M Ø dt

R_t * J d² α dα

U(t) = * + C_EØ

C_mØ dt² dt

CZŁON INERCYJNY II RZĘDU

Równanie różniczkowe: T₁T₂y'' + T₁y_t' + y = ku

Lub

T_AT_By'' + (T_A+T_B) y' + y = ku

K - współczynnik wzmocnienia określony jako stosunek odpowiedzi y do wymuszenia u w stanie ustalonym.

T₁T₂T_AT_B - stałe czasowe.

K

Transmitacja: G(s) =

T₁T₂S² + T₁S + 1

Lub

K

G(s) =

T_AT_BS² + (T_AT_B) s + 1

T₁ - 4T₂ >=0 __

____ 1 √T₁

T_{B =} √T₁T₂ , S = __

2 √T₂

_____ T_A + T_B

T₀ = √T_AT_B , ζ = _____ , K = K_A - K_B

2 √T_AT_B

K_A

G₁(s) =

1 + STA

K_B

G₂(s) =

1 + STB

Przykład:

CZWÓRNIK R,C,

dI(t) 1 _t

U_we(t) = R * I(t) + L + ∫ I(t)dt

dt c ⁰

1 _t dU_wy

U_wy(t) = ∫ I(t) dt c = I(t) różniczkuje raz jeszcze

C ⁰ dt

dU_wy d²U_wy d²U_wy dI

U_we(t) = RC * + L C + U_wy C = =

dt dt dt dt

To czy układ będzie inercyjny II rzędu, czy oscylacyjny zależy od parametrów

CZŁON OPÓŹNIAJĄCY

Równanie różniczkowe: y(t) = ku( t - T₀)

K - współczynnik wzmocnienia określony jako stosunek odpowiedzi y do wymuszenia u dla

t >T₀

T₀ - czas opóźnienia

Charakterystyka skokowa: h(t) = k 1(t - T₀)

Odpowiedź impulsowa: g(t) = kδ(t - T₀)

Transmitacja: g(s) = ex (-sT₀)

CZŁON OSCYLACYJNY

Odpowiada na wymuszenie

1. Tłumione

2.Nie Tłumione

3. Narastanie.

TRANSMITACJA OPERATOROWA:

Transformata Laplace'a: _∞

F(s) = ∫ f(s) e^-st = L[ f(t) ]

⁰

Orginały Laplace'owskie ( f(t) będzie orginałem, jak spełni 3 warunki):

1. f(t) = 0 t<0 Obserwacje prowadzimy w przód, nie bierzemy pod uwagę

przeszłości.

2. Funkcja ciągła i monotoniczna przedziałami.

3. f(t) <= m* e ^αt Można zrobić na funkcjach , które rosną, ale nie szybciej jak funkcja wykładnicza( np. e^t)2 nie da się jej ograniczyć);

Własności transformaty Laplace'a:

1. Złożenie dwóch operacji

L^-1[L(f(t))] - f(t) , L[L^-1(F(s))] = F(s)

α(1(t)) = 1/s , α^-1(1/s) = 1(t)

1 1

L( e^-αt * 1(t)) = , L^-1 ( ) = e^-αt * 1(t)

S+α S+α

Funkcje określam dla czasu T = 0

2. Liniowość:

Obowiązuje zasada superpozycji( odpowiedź na wymuszenie jest odpowiedzią na sumę tych wymuszeń.

L [a₁f₁(t) + a₂f₂(t)] = a₁L[f₁(t)] + a₂L[f₂(t)]

Przykłady:

( e^jωt = cos ωt + j sin ωt)

( e^-jωt = cos ω - j sin ωt)

1

sin ωt = ( e^jωt - e^-jωt)

2j

1 1 1 1 2jω ω

L { sin ωt * 1(t) } = ( - ) = * =

2j s-jω s+jω 2j s² + ω² s² + ω²

ω

L { sin ωt } =

s² + ω²

4

sin 4t =

s² + 16

1 3

L^-1 ( ) = L^-1 ( ⅓ * ) = ⅓* sin 3t

s² + 9 s² + 9

3. Holomorficzność (funkcja, która ma pochodne):

dF(s) dF(s)

= -∫ t f(t) e^-st dt czyli L[t f(t)] = -

ds. ds.

oraz

n! n!

L(fⁿ) = , L(ten^-αt) =

Sⁿ⁺¹ (s + α)ⁿ⁺¹

L { t*1(t)} = 1/s

-1 1

- =

s² s²

s+2 1 3 1 1 1 3 1

L^-1 ( = L^-1 (-2 * + * + * ) = (-2 + e^t+ e^-t)1(t)

s(s² - 1) s 2 s-1 2 s+1 2 2

3. Transformata pochodnej:

ω s

L (cos ωt) = L (1/ω(sin ωt)') = 1/ω *(s*L(sin ωt) - sin 0 ) = 1/ω * s * =

s² + ω² s²+ω²

Idea rachunku operatorowego

Mamy problem w dziedzinie czasu

Równanie L równanie wyznaczanie L wyznacznie

Dla orginału dla obrazu obrazu oryginału

Przykład: dI(t)

U *1(t) = R*I(t) + L

dt

równanie obrazu bo oper, różniczkowemu

odpow. mnożenie przez s.

*U1/s = R * I(s) + L*s*I(t)

u 1

I(s) = *

S R*SL

Rozw w dziedzinie Laplace'a

Faza końcowa - wyznaczenie oryginału.

1 K/R U/R

= 1/s + = -

s+R/L S s + R/L

I(t) = U/R * (1 - e^-(R/L)*t) * 1(t)

pisane

---