Tomasz Migdał gr. R33
Wstęp
W trakcie ćwiczenia badane przez nas były trzy pierwiastki promieniotwórcze: kobalt (Co), Cez (Cs), i Sód(Na). Pierwiastki umieszczane były w komorze z licznikiem scyntylacyjnym. Analizatorem amplitudy był komputer klasy PC wyposażony w kartę z przetwornikiem A/C. Wielkością obserwowaną była liczba zliczonych impulsów elektrycznych o określonej amplitudzie ( cały zakres amplitud był podzielony na jednakowe części - kanały ).
Opracowanie ćwiczenia:
Na początku należało wyskalować spektrometr scyntylacyjny, co oznacza przypisanie poszczególnym kanałom konkretnych energii. Z trzech pierwiastków promieniotwórczych dla których znane są energie przejść elektronów między danymi powłokami : ![]()
![]()
![]()
należało wybrać jeden pierwiastek, który umożliwi wyskalowanie spektrometru.
Z porównania schematów obrazujących opis energetyczny przejść elektronówmiędzy powłokami wynikało, iż najwłaściwszy do wyskalowania jest preparat kobaltowy. Charakteryzuje się tym, iż ma elektrony na powłoce o najwyższej energii oraz ulega dwóm przemianom (wzbudzone jądro niklu emituje dwa kwanty γ o różnych wartościach energii1.33 MeV oraz 1,17 MeV- fotopiki o numerach 1 i 3). Pozwala to na wyskalowanie spektrometru - dzięki większej energii charakterystyka może być dokładniej wyskalowana, natomiast dwie przemiany ułatwiają wyznaczenie prostej skalowania - dodatkowy punkt wykorzystywany do wyznaczenia prostej.
I tak na podstawie trzech punktów wyznaczamy prostą skalowania:
E=aN+b
,gdzie
E- energia odpowiadająca kwantowi N
N- numer kanału
a=(4,205±0,015)*10-4 MeV
b=(-5.7±0,4)*10-2 MeV
Prosta skalowania jest przedstawiona na rysunku. Za jej pomocą można wyznaczyć energię dowolnych punktów widma energetycznego dla dowolnych nieznanych izotopów. Poniższe tabele przedstawiają wyniki pomiarów punktów składających się na określone widma. Zostały także wyznaczone błędy energii:
ΔE= aΔN +NΔa + Δb
, błąd wartości N czyli ustawienia kanału uznam za ±12, ponieważ porównując wartość wyznaczoną bezpośrednio dla widma sodu ( 6 pik) z wartością średnią wyznaczoną pośrednio. Były to wartości następujące :
6 pik - 1309 5- 1374 7- 1236 średnia pików 5 i 6 to 1305
błąd popełniany przez wykonującego ćwiczenie wyniósł 4, dlatego zakres błędu określiłem jako 3σ czyli 12.
Dla Co
Nr pkt. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
E[MeV] |
1.33 |
1.26 |
1.17 |
1,00 |
0.95 |
0.91 |
0.21 |
0,03 |
ΔE*10-3 [MeV] |
15 |
14 |
14 |
13 |
13 |
13 |
10 |
10 |
Błąd dla wartości początkowej to ok 1% natomiast rośnie dla małych wartości energii do ok 30 %
Dla Cs
Nr pkt. |
1 |
2 |
3 |
4 |
5 |
6 |
E[MeV] |
0,65 |
0.50 |
0.46 |
0.44 |
0.17 |
0.03 |
ΔE*10-3 [MeV] |
12 |
12 |
11 |
11 |
10 |
10 |
Dla Na
Nr pkt. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
E[MeV] |
1,27 |
1,10 |
1,06 |
1,01 |
0,52 |
0,49 |
0,46 |
0,35 |
0,32 |
0,28 |
0,24 |
0,17 |
0,04 |
၄ [Mev] |
14 |
14 |
14 |
13 |
12 |
12 |
11 |
11 |
11 |
11 |
11 |
10 |
10 |
Zdolność rozdzielcza spektrometru wyznaczana jest na podstawie błędu jaki otrzymamy na podstawie otrzymanych wyników poszczególnych energii i ich błędów widm energetycznych:
R=ΔE/E *100%
Preparat kobaltowy
pik 1 R=1,2 %
pik 8 R=33,4 %
Preparat cezowy
R2= 2,4%
Preparat sodowy
R6= 2,3 %
Kobalt:
Kobalt jako jedyny z trzech izotopów podczas rozpadu emitował dwa kwanty γ o różnych wartościach energii. Odpowiadają temu punkty 1 i 3 o różnych wartościach energii 1.33 MeV oraz 1,17 MeV wartości te zgadzają się z różnicami energii pomiędzy poszczególnymi poziomami jakie występują przy rozkładzie atomów Co na Ni* i Ni zachodzącym jako rozpad -β ![]()
. Pik 8 powstaje na wskutek wybijania elektronów z powłoki K. Gdy energia kwantu γ jest większa niż energia wiązań elektronów na tej powłoce to następuje wybijanie elektronów z powłoki zgodnie ze wzorem : Ee=hv-Wn. Takiemu zjawisku towarzyszy zapełnienie tej powłoki przez jeden z elektronów z wyższych powłok. Elektron obdarzony energią ze swojej powłoki zapełniając powłokę o niższej energii wydziela różnicę w postaci fali elektromagnetycznej. Po porównaniu energii jaka wydziela się podczas tego zjawiska można przyjąć iż jest to promieniowanie rentgenowskie (X). Pozostałą część widma należy rozpatrywać jako pochodząca od efektu Comptona. W wyniku rozproszenia Comptonowskiego kwanty γ przekazują tylko część swojej energii elektronowi mieszczącej się w przedziale 0≤Ee≤Eemax; jest to związane z kątem pod jakim następuje zderzenie. Maksimum występuje dla kąta = 180° Dzieje się tak dlatego, że zgodnie z teorią kwantową zjawisko Comptona jest wynikiem sprężystego zderzenia fotonu ze swobodnym elektronem. W takim to zderzeniu zgodnie z zasadami zachowania energii i pędu foton przekazuje tylko część swej energii i pędu. Maksimum ![]()
daje się wyznaczyć z wcześniej wymienionych zasad i wynosi ono: 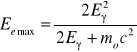
, uzyskujemy to zakładając:
dla kobaltu jest to 0,96 MeV dla Eγ=1,17; oraz 1,12 dla Eγ=1,33, to właśnie opierając się na założeniu, iż fotony wybijają elektrony pod różnym kątem wnioskuję iż stąd powstaje widmo ciągłe. Pozostałą część energii kwant może przekazać w ponownym zderzeniu z kolejnym elektronem w wyniku, którego mogą zajść zjawiska fotoelektryczne lub Comptona. Zawsze jest spełniona tu zasada zachowania energii Eγ=Ee+E'γ.
Prosta określona punktami 4,5,6 jest krawędzią zwaną jako Comptonowska określa maksymalne wartości energii elektronu uzyskane na wskutek efektu Comptona. Pik nr 7 powstał na wskutek efektu Comptona występującego dla energii określonej jako 0,21 MeV. Foton o energii 1,17 lub 1,33 MeV zderza się z elektronem i przekazując mu część energii posiadając teraz 0,21 MeV sam wywołuje efekt fotoelektryczny.
Całość widma jest sumą widma ciągłego oraz pików - czyli pewnych wartości energii - widmo uwarunkowane jest zasadami zachowania energii i pędu.
Cez
Na podstawie wstępnego porównania widoczne jest iż występuje podobieństwo do widma energii kobaltu. Cez w wyniku rozpadu -β przechodzi w Bar (B) o wzbudzonym jądrze (ok. 92% przemian) Wzbudzone jądro Ba* przechodząc do stanu podstawowego emituje kwant γ o energii 0,66 MeV ( pierwszy pik na wykresie) Fotopik powstał na skutek zajścia zjawiska fotoelektrycznego. Kwanty γ przekazały energię elektronom na jednaj z powłok. Elektrony te powodując jonizację powodowały pośrednio zliczanie impulsów przez spektrometr. Brakuje tu piku 3 z widma kobaltu, a wynika to z jednej możliwości przejścia Cezu w Bar. Punkt 5 (rozproszenie wsteczne - elektrony zostały odbite pod kątem Π) odpowiada punktowi 7 widma kobaltu. Po zderzeniu się fotonu o energii 0,65 MeV z elektronem i przekazaniu mu części energii następuje kolejne zderzenie się tego fotonu już o energii 0,17 MeV i wywołanie efektu fotoelektrycznego. Pik 6 to tak jak w kobalcie punkt 8 - efekt fotoelektryczny w wyniku, którego po zapełnieniu przez elektron dziury po wybitym przez foton elektronie następuje wydzielenie się nadmiaru energii w postaci fali elektromagnetycznej, której energia wskazuje na to, iż jest to promieniowanie X. Punkt 3 to granica efektu Comptona - tj. maksymalna energia, jaką mogą otrzymać elektrony od kwantów γ. Punkty 2-3-4 tworzą krawędź Comptonowską dla przedziału energii E∈(0,46;0,66)MeV. Określa ona maksymalne wartości energii elektronu uzyskane na wskutek efektu Comptona. Rozmycie krawędzi Comptonowskiej może wynikać z tego, iż rozproszone elektrony mogą wywoływać później zjawisko fotoelektryczne, co rozmywa krawędź.
Sód
Widmo energii dla sodu jest odmienne niż widma Co i Cs. Jest tak dlatego, iż podczas rozpadu +β sodu na Ne mogą zajść dwa rodzaje zmian energetycznych - pierwsza to rozpad +β bezpośrednio na Neon bez wydzielenia kwantu γ druga możliwość to częściowy rozpad +β, a następnie wydzielenie kwantu γ. Odmienne zjawisko występuje w piku 6, dla którego energia wynosi 0,49 MeV, zaś uzyskana drogą uśrednienia pików 7 i 5 wg wzoru Eśr= (E1+E2)/2 wynosi 0,4916 MeV. Po przemianie -β(![]()
) anihiluje pozyton z elektronem tworząc dwa kwanty o energiach 0,51 MeV każdy, kwanty te wywołują zjawisko fotoelektryczne. Powstałe kwanty γ również mogą wywołać efekt Comptona. Obserwowany fotopik odpowiada również zjawisku rozproszenia wstecznego. Prosta utworzona z punktów 10-11-12 odpowiada zjawisku comptona w którym biorą udział wcześniej wymienione kwanty.
Obserwujemy tu również krawędzie comptonowskie 2-3-4, 8-9-10.
Krawędź 2-4 reprezentuje elektrony, na których rozproszyły się kwanty γ, powstałe w wyniku efektu Comptona (wcześniejsze zderzenie się kwantu o większej energii z elektronem i oddanie mu części energii), jest ona pochylona na wskutek wielokrotnego rozproszenia Comptona. Druga krawędź ma taką samą istotę, jednak reprezentowana jest przez efekty fotoelektryczne, powstające na wskutek zderzeń fotonów, które już wcześniej oddały część energii elektronom na wskutek wcześniejszych zderzeń.
Widoczny jest również pik 1 dla kwantów o energii 1,274 MeV, co jest równe wartości teoretycznej - występuje tu zjawisko fotoelektryczne, w którym cała energia kwantu została przekazana elektronowi.
Pik 12 reprezentuje zjawisko rozpraszania wstecznego. Po zderzeniu się fotonu o energii 0,65 MeV z elektronem i przekazaniu mu części energii następuje kolejne zderzenie się tego fotonu już o energii 0,17 MeV i wywołanie efektu fotoelektrycznego. Fotopik 13 to wydzielenie się fali elektromagnetycznej na wskutek oddania nadmiernej energii przez elektron, zajmujący wolne miejsce w powłoce o niższej energii - z porównania energii wynika, iż jest to promieniowanie X.
ROZPADY -β i +β
Terminem rozpad β oznaczamy przemiany jądrowe
-β ![]()
rozpad elektronowy - charakterystyczny dla promieniotwórczości sztucznej jak i naturalnej. Neutron tu przekształca się samorzutnie w proton. Jest możliwa zarówno w jądrze jak i poza nim.
+β ![]()
rozpad pozytonowy - charakterystyczny tylko dla promieniotwórczości sztucznej tj pojawienia się promieniowania na wskutek pojawienia się innych cząstek. Może zachodzić jedynie w jądrze, gdzie energia niezbędna do jej zajścia może zostać pobrana od sąsiednich cząstek.
4
LABORATORIUM FIZYKI II Ćw. 11
Badanie właściwości promieniowania gamma za pomocą spektrometru scyntylacyjnego.
Wyszukiwarka