Wykład 6: Testy zgodności dopasowania

TESTY ZGODNOSCI

• Te metody znajdują zastosowanie przy analizie danych w skali nominalnej, pozwalają sprawdzić czy obserwowany rozkład zliczeń (nigdy częstotliwości lub proporcji) zgadza się z rozkładem hipotetycznym.

• Najbardziej znaną techniką analizy jest test zgodności chi-kwadrat (χ²).

WPROWADZENIE

• Załóżmy, że genetyk w ramach eksperymentu skrzyżował mieszaną populację F₁ i otrzymał potomstwo F₂ z 90-oma potomkami, z których n₁=80 ma fenotyp typu

wild-type, a u n₂=10 zaobserwowano mutacje.

• Genetyk, zgodnie z prawem dziedziczenia, założył stosunek fenotypów 3:1, ale rzeczywisty stosunek wyniósł 80/10 = 8:1.

• Spodziewane wartości p i q wynoszą

odpowiednio dla wild-type i mutantów.

• Używamy symbolu „daszek” żeby zaznaczyć hipotetyczne lub oczekiwane wartości proporcji.

• Obserwowane proporcje tych dwóch klas wynoszą odpowiednio

• Innym sposobem pokazania różnic między wartościami oczekiwanymi a obserwowanymi to wyrazić je w zliczeniach (niektórzy nazywają je częstościami).

• Obserwowana liczba zliczeń to n₁=80 i n₂=10 dla dwóch fenotypów.

• Oczekiwana liczba zliczeń to

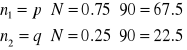
gdzie N to liczność próby - liczba potomków.

• Czy obserwowane odchylenie od hipotezy 3:1 jest tak wielkie, że praktycznie nieprawdopodobne?

• Innymi słowy, czy zaobserwowane dane wystarczająco różnią się od wartości oczekiwanych, żeby odrzucić hipotezę zerową?

WYKORZYSTANIE FUNKCJI GĘSTOŚCI PRAWDOPODOBIEŃSTWA

• Rozkład, w którym p jest prawdopodobieństwem naturalnego fenotypu, a q zmutowanego, jest rozkładem dwumianowym.

• Możemy wyliczyć prawdopodobieństwo otrzymania wyniku 80 naturalnych i 10 zmutowanych fenotypów, podobnie jak dla wszystkich „gorszych” przypadków w próbie 90 potomków dla

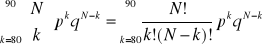
jest równe dopełnieniu do jedności wartości dystrybuanty.

• Wyliczona wartość jest prawdopodobieństwem 0.00084895 uzyskania wyniku co najmniej tak odległego od hipotezy jak obserwowany.

• Zauważ, że jest to test jednostronny; alternatywna hipoteza mówi, że jest więcej potomków z fenotypem typu wild-type, niż liczba określona przez prawo Mendla.

• Zaobserwowana próba jest dość rzadkim wynikiem i możemy wnioskować, że to jest istotne odchylenie od oczekiwań.

ZASTOSOWANIE PRZEDZIAŁÓW UFNOŚCI

• Jest to łatwiejsze podejście, wymagające obliczenia przedziałów ufności dla dwumianowych proporcji i przeprowadzenia wnioskowania statystycznego w oparciu o uzyskane wyniki.

TEST ZGODNOŚCI

• Opracujemy trzecie podejście do oceny hipotezy zerowej - poprzez testy zgodności dopasowania.

• Tabela ilustruje jak postępować.

Test G

• Test bazuje na logarytmie stosunków wiarygodności

Fenotypy	Obserwowane zliczenia	Obserwowane proporcje	Oczekiwane proporcje	Oczekiwane zliczenia	Stos.zliczeń obserwowanych do oczekiwanych
Wild-type	80	0.89	0.75	67.5	1.185185	13.59192
Mutant	10	0.11	0.25	22.5	0.444444	-8.10930
Suma	90	1.0	1.0	90.0		Ln L=5.48262

• Test G może być skonstruowany następująco:

Prawdopodobieństwo zaobserwowania wyniku zgodnego z próbą, przy założeniu, że parametry p i q rozkładu są równe proporcjom w próbie, wynosi

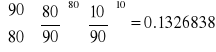
Prawdopodobieństwo zaobserwowania wyniku zgodnego z próbą, przy założeniu proporcji Mendla, jest równe

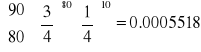
Jeśli obserwowane proporcje są zgodne z proporcjami z hipotezy zerowej, obydwa obliczone wcześniej prawdopodobieństwa będą równe, a ich stosunek L równy 1.

Im większa różnica między proporcjami, tym większe odchylenie L od 1.

Stosunek tych dwóch prawdopodobieństw lub wiarygodności może być użyty w formie statystyki do zmierzenia zgodności między zliczeniami w próbie a oczekiwanymi.

Test G (logarytmiczny test ilorazu wiarygodności) to test oparty właśnie na takim stosunku.

Zostało dowiedzione, że rozkład

G = 2 ln L

może być przybliżony przez rozkład χ² z jednym stopniem swobody.

W naszym wypadku

G = 2 ln L = 10.96524

Jeśli porównamy tę wartość z rozkładem χ² o jednym stopniu swobody (df), otrzymujemy że wynik jest istotny statystycznie(p-wartość = 0.000928 < 0.001)

ROZKŁAD CHI-KWADRAT, 1df

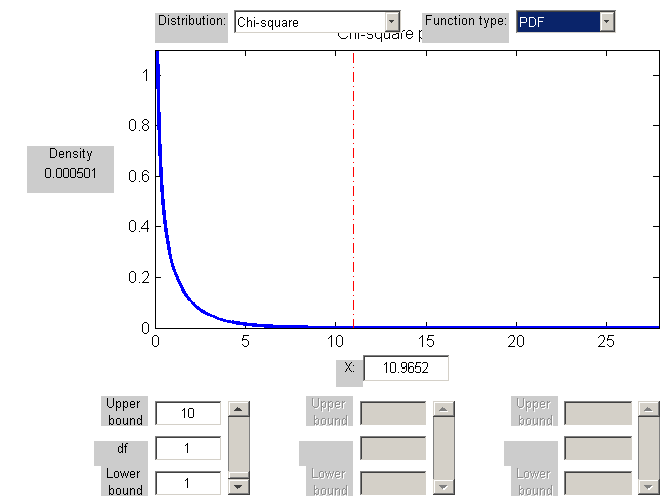
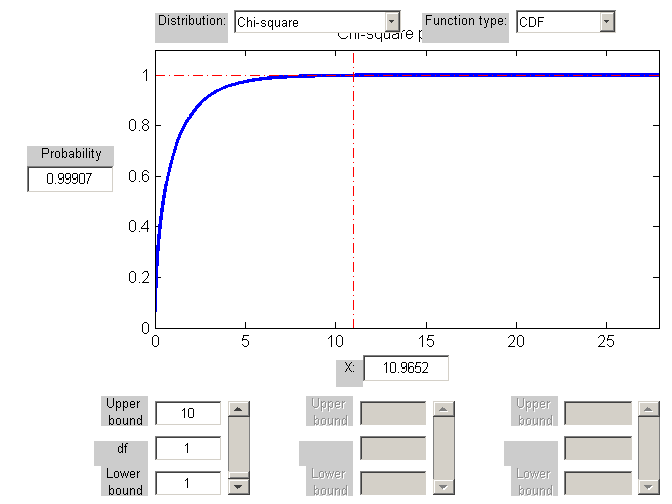
10.96524

Wzór obliczeniowy

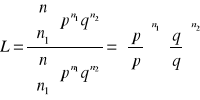
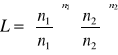
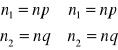
Ponieważ to

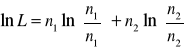
i

TEST G DLA WIĘCEJ NIŻ 2 KLAS

• Test zgodności można zastosować do rozkładu z większą liczbą klas niż dwie.

• Obliczamy stosunki obserwowanych zliczeń do oczekiwanych, logarytmujemy i mnożymy przez liczność obserwowaną.

• Suma daje ln L, podczas gdy rozkład G = 2 ln L w przybliżeniu pokrywa się z rozkładem chi-kwadrat z a-1 stopniami swobody, gdzie a to liczba klas.

Przykład 1

• Badanie miejsc powrotu łososi na tarło - strumień macierzysty versus sąsiednie.

N = 200 ryb	Strumień macierzysty	Strumień 1	Strumień 2	Strumień 3	Strumień 4
Obserwowane zliczenia	135	15	17	10	23

Hipoteza:

H₀: Łososie wybierają strumień macierzysty w 75% przypadków; pozostałe w 25% przypadków (6.25% na każdy z czterech).

H_a: nie H_o

• Można sformułować hipotezę zerową w inny sposób

H₀: próba pochodzi z populacji łososi z proporcjami 12:1:1:1:1 wyboru strumienia macierzystego i alternatywnych.

H_a: nie H₀.

	Obserwowane zliczenia	Oczekiwane zliczenia	Stosunek
Strumień domowy	135	150	0.90	-14.2237
Strumień 1	15	12.5	1.20	2.7348
Strumień 2	17	12.5	1.36	5.2272
Strumień 3	10	12.5	0.80	-2.2314
Strumień 4	23	12.5	1.84	14.0246
Suma	200	200		ln L = 5.5315

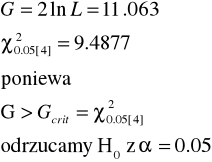
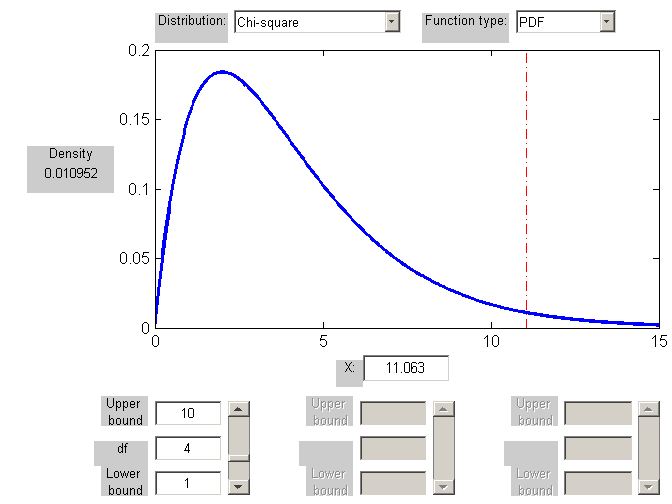
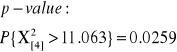
TEST CHI-KWADRAT ZGODNOSCI DOPASOWANIA

• To tradycyjne podejście, stosowane w znacznej liczbie publikacji naukowych.

• Jeszcze raz spójrzmy na eksperyment genetyka z wynikiem 80 potomków wild-type i 10 mutantów.

• Najpierw obliczamy odchylenia zliczeń obserwowanych od zliczeń oczekiwanych i podnosimy je do kwadratu.

• Następnie obliczamy względne kwadraty odchyleń - dzielimy je przez liczbę zliczeń oczekiwanych.

• Ostatecznie sumujemy otrzymane wartości.

• Otrzymana statystyka jest nazywana statystyką chi-kwadrat X², ale ma ona jedynie rozkład przybliżony do rozkładu X² z jednym stopniem swobody.

• Niektórzy nazywają statystykę X² statystyką Pearsona.

• Test chi-kwadrat jest zawsze jednostronny!!

Fenotypy	Obserwowane zliczenia	Oczekiwane stosunki	Oczekiwane zliczenia	Odchylenia do kwadratu	Względne kwadraty odchyleń
Wild-type	80	0.75	67.5	156.25	2.3148
Mutant	10	0.25	22.5	156.25	6.9444
Suma	90	1.0	90.0		X2 = 9.2592

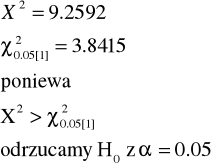
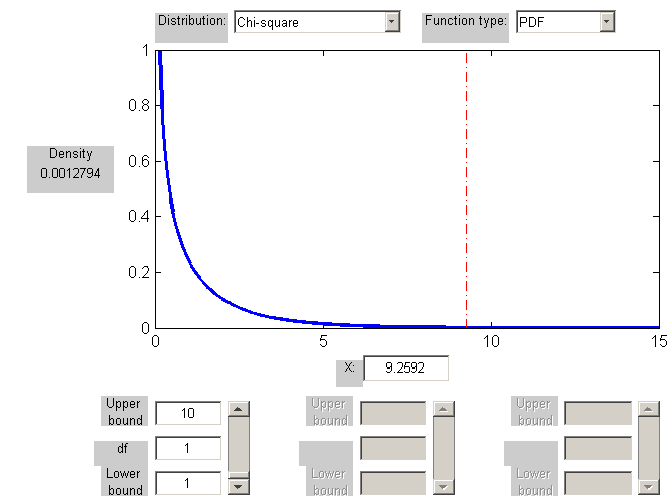
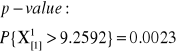
TEST CHI-KWADRAT ZGODNOSCI DOPASOWANIA DLA WIĘCEJ NIŻ DWÓCH KLAS

• Test dopasowania chi-kwadrat można zastosować dla więcej niż dwóch klas.

• Oblicz:

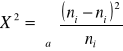
• Statystyka X² ma w przybliżeniu rozkład chi-kwadrat z a-1 stopniami swobody, gdzie a to liczba klas.

Przykład 1 - cd.

	Obserwowane zliczenia	Oczekiwane zliczenia	Odchylenie	Względne odchylenia
Strumień macierzysty	135	150	225	1.50
Strumień 1	15	12.5	6.25	0.50
Strumień 2	17	12.5	20.25	1.62
Strumień 3	10	12.5	6.25	0.50
Strumień 4	23	12.5	110.25	8.82
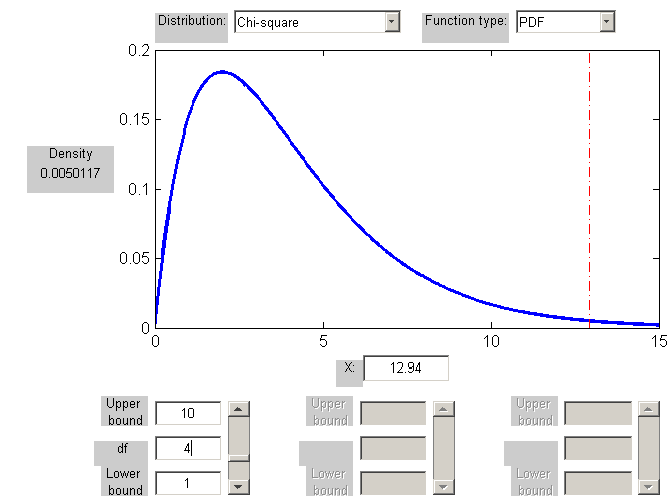
Suma	200	200		X2=12.94

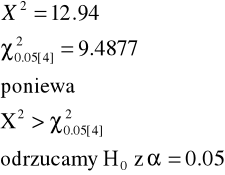
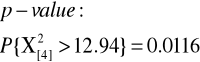
TESTOWANIE CZĄSTKOWE

• W naszym przykładzie o łososiach, wygląda na to, że liczba ryb płynąca do strumienia 4 spowodowała odrzucenie H₀.

• Dlatego stosujemy analizę cząstkową.

• Przetestujmy H₀: Próbka pochodzi z populacji z proporcjami 12:1:1:1 wyboru strumienia macierzystego i alternatywnych 1-3.

Przykład 1 - testowanie cząstkowe

	Obserwowane zliczenia	Oczekiwane zliczenia	Odchylenie	Względne odchylenie
Strumień macierzysty	135	177*12/15=141.6	43.56	0.3076
Strumień 1	15	177*1/15=11.8	10.24	0.8678
Strumień 2	17	11.8	27.04	2.2915
Strumień 3	10	11.8	3.24	0.2746
Suma	177			X2=3.7415

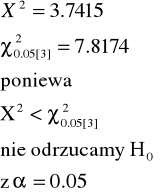
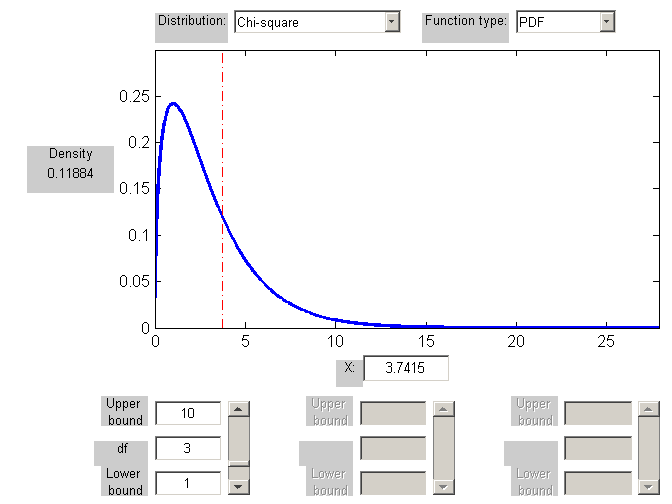
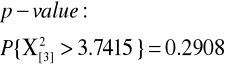
KOREKTY NA NIECIĄGŁOŚĆ

• Wartości statystyk G lub X² liczone na podstawie danych mają rozkład dyskretny.

• Jednak teoretyczny rozkład chi-kwadrat jest ciągły.

• Z wartościami nieskorygowanymi można łatwiej fałszywie odrzucić H₀ (błąd I-szego rodzaju jest większy niż zamierzony).

• W przypadku dwóch klas jest to poważny problem. Jeśli N<200 musimy stosować korekty na nieciągłość.

• Test G - korekta Williams'a

• Test X² - korekta Yates'a

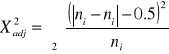
TESTOWANIE DLA INNYCH ROZKŁADÓW

• Możemy zastosować przedstawione testy zgodności do weryfikacji hipotez o rozkładach innych niż dwumianowy.

• Jeśli szacujemy parametry rozkładu na podstawie danych, musimy poprawnie ustalić liczbę stopni swobody.

Rozkład	Parametry szacowane na podstawie próby	Liczba df
Dwumianowy	p	a-2
Normalny	μ,σ	a-3
Poissona	μ	a-2

TEST KOŁMOGOROWA- SMIRNOWA ( KS )

• Nieparametryczny test, stosowany do analizy zmiennych o ciągłych rozkładach częstości, mający większą moc niż testy zgodności G i X², jest nazywany testem
  Kołmogorowa-Smirnowa (KS).

• Test KS jest szczególnie przydatny dla małych prób, nie jest wskazane grupowanie klas.

• Test jest oparty na różnicach między dwiema dystrybuantami rozkładów obserwowanych i oczekiwanych.

• Powinien być stosowany dla danych dyskretnych w skali porządkowej.

• Jest lepszy niż zwykły test chi-kwadrat i test G, ponieważ uwzględnia relację porządku kategorii.

• Test dla dyskretnych danych analizuje skumulowane zliczenia obserwowane i oczekiwane oraz przyjmuje za statystykę największą różnicę między nimi:

Ta wartość jest porównywana z wartością krytyczną, gdzie k=liczba kategorii, N=liczność próby, α = poziom istotności alfa

Przykład 2 - dane dyskretne

• Chcemy sprawdzić czy insekty mają preferencje związane z natężeniem oświetlenia - czy ich liczność jest równomiernie rozłożona wzdłuż gradientu światła.

• Nie można zmierzyć w skali liniowej różnic gradientu światła, ale można określić, że mniejsze liczby odpowiadają mniejszemu natężeniu światła niż większe liczby.

• H₀: Liczba insektów jest równomiernie rozłożona wzdłuż gradientu światła

• H_a: nie H₀

• Ustalamy α = 0.05

N=65	Ciemno - 1	2	3	4	Jasno - 5
Obserwowane zliczenia	0	7	6	38	14
Oczekiwane zliczenia	13	13	13	13	13
Obserwowane kumulatywne zliczenia	0	7	13	51	65
Oczekiwane kumulatywne zliczenia	13	26	39	52	65
|di|	13	19	26	1	0

• Statystyka testowa d_max = 26

• Wartość krytyczna d_{max,0.05,5,65} = 10 (patrz tabela)

• Zasada decydowania: odrzucenie H₀ jeśli d_max≥10; w przeciwnym razie przyjęcie H₀.

• Ponieważ 26>10 (p<0.001), odrzucamy H₀.

• Wniosek:

Zaobserwowane dane nie mają rozkładu równomiernego wzdłuż uporządkowanych poziomów natężenia światła (p<0.001).

TEST KS ZGODNOŚCI DOPASOWANIA - dane ciągłe

• Wykorzystujemy własność, że pomimo iż skumulowane oczekiwane zliczenia opisane są funkcją ciągłą, największa różnica między zliczeniami obserwowanymi a oczekiwanymi występuje w punktach nieciągłości - jest liczona zarówno przed jak i po tym jak dystrybuanta zliczeń obserwowanych idzie krok w górę.
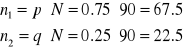
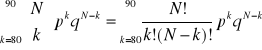
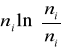
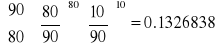
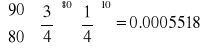
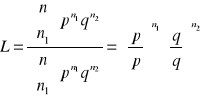
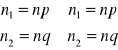
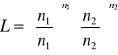
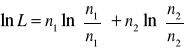
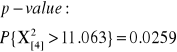
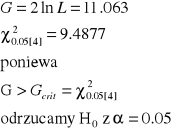
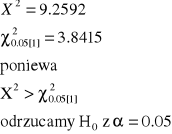
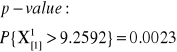
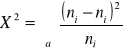
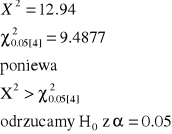
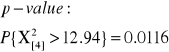
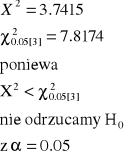
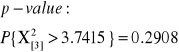
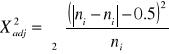