WOJSKOWA AKADEMIA TECHNICZNA

WYDZIAŁ MECHATRONIKI

ZAKŁAD INŻYNIERII BEZPIECZEŃSTWA

ĆWICZENIE LABORATORYJNE

Temat: Badanie stabilności układów dynamicznych.

Prowadzący: ppłk. dr inż. Sławomir Stępień

Ocena:

WYKONALI: Gospodarczyk Karol

Janczewski Damian

Kopaczewski Adam

Kutkowski Kamil

Łuniewski Sławomir

Mrozek Rafał

Rupiński Piotr

Żebrowski Rafał

Gaworski Bartosz

Cebula Paulina

Choiński Igor

Grupa A8X4S1 Warszawa 2010

1. Część teoretyczna

Serwomechanizm jest to zamknięty układ sterowania przemieszczeniem (układ automatyki), o strukturze typowego układu regulacji. Wartość wzorcowa porównywana jest z przetworzonym przez przetwornik bieżącym sygnałem wyjściowym i powstały w ten sposób uchyb podawany jest na człon korekcyjny, a dalej na wzmacniacz. Wzmocniony sygnał trafia do siłownika, którego przemieszczenie jest wartością wyjściową układu. Zadaniem serwomechanizmu jest likwidacja błędów regulacji (uchybu przemieszczenia), powstających na skutek zmian wielkości wzorcowej, a więc klasyfikujemy go jako układ nadążny.

Schematy blokowe układu:

Rys 1. Schemat blokowy serwomechanizmu.

Rys 2. Schemat blokowy serwomechanizmu po przekształceniach.

Wyprowadzenie zależności na transmitancje G_yx, G_yf :

G(s)=

G(s)=

Przekształcona transmitancja układu:

G_yx(s) =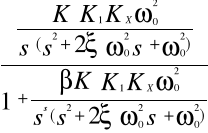
* α =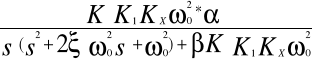

G_yf(s) =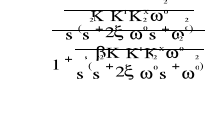
*
=

=

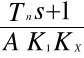
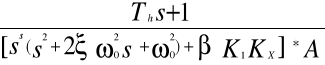
2. Część praktyczna

Zapis opracowanego programu w matlab, mającego na celu symulację badanego układu dynamicznego z serwomechanizmem, wygląda następująco:

alfa=1;

K1=2;

Kx=1.5;

Th=0.1;

A=0.001;

Kv=2.5;

Tm=0.2;

b=0.2;

beta=1.8; - paramet odpowiedzialny za stabilność

K=A/(1+A*Kv*b);

Ksi=(Th+Tm)/(Th*Tm);

omega=(1+A*Kv*b)/(Th*Tm);

Lo=[alfa*K1*Kx*K*omega];

Mo=[1 Ksi omega 0];

tf(Lo,Mo)

Lz=[alfa*K1*Kx*K*omega];

Mz=[1 Ksi omega beta*K1*Kx*K*omega];

tf(Lz,Mz)

figure;

impulse(Lo,Mo)

grid on;

figure;

impulse(Lz,Mz)

grid on;

figure;

bode(Lo,Mo)

grid on;

figure;

bode(Lz,Mz)

grid on;

figure;

nyquist(Lo,Mo)

grid on;

figure;

nyquist(Lz,Mz)

grid on;

figure;

step(Lo,Mo)

grid on;

figure;

step(Lz,Mz)

grid on;

Kolorem zielonym oznaczone są zmienne o określonej wartości, bądź wartości podanej przez prowadzącego, które nie ulegają zmianie w czasie przeprowadzania badaania stabilności układu dynamicznego.

Kolorem żółtym oznaczone są funkcje pakietu Matlab - Simulink, które pozwalają na wykreślanie charakterystyk badanego układu dynamicznego.

Uzyskane wybrane wykresy obrazujące zmianę stabilności układu w zależności od przyjętej wartości zmiennej „beta“:

Wykresy:

Wyk 1. Drogi pierwiastków dla układu otwartego - stabilnego.

Wyk 2. Drogi pierwiastków dla układu otwartego - niestabilnego.

Wyk 3. Charakterystyka skokowa dla układu zamkniętego niestabilnego.

Wyk 4. Charakterystyka skokowa dla układu zamkniętego stabilnego.

Wyk 5. Charakterystyka skokowa dla układu otwartego stabilnego.

3. Wnioski

Układy z serwomechanizmami mają szerokie zastosowanie w technice i zazwyczaj dzielone są na dwie klasy problemów. Pierwszą z nich jest sterowanie z otwartą pętlą regulacji. Tego typu układy stosowane są w serwomechanizmach sterujących urządzeniami gdzie przez użytkownika wymagane jest dokładne śledzenie trajektorii działania danego urządzenia.

W ćwiczeniu zauważyliśmy że sygnał wejściowy nie zależy od aktualnej wartości sygnału wyjściowego, z uwagi na brak sprzężenia zwrotnego, zależy on jedynie od wewnętrznego stanu obiektu. Przebieg sygnału następuje tylko w jednym kierunku, od wejścia do wyjścia. Nie istnieje możliwość tłumienia nieznanych zakłóceń oraz osiągnięcie wartości zadanej nie może być zweryfikowane. To sprawia, że układ otwarty może być stosowany w przypadku prostych obiektów, dla których znany jest dokładny model matematyczny. W przypadku znanej wartości zakłócenia układ otwarty może być użyty do jego kompensacji.

Drugim problemem jest tłumienie i eliminacja zakłóceń charakterystycznych dla serwomechanizmów. W tym celu stosuje się pętle sprzężenia zwrotnego, charakteryzują się poprawieniem odpowiedzi czasowych, redukcją błędów w stanie ustalonym oraz zmniejszeniem wrażliwości na zmiany parametrów obciążenia, zakłócenia i modelowania w porównaniu z układami z pętlą otwartą. Z wykresów numer 1,2, 3 i 4 możemy wywnioskować, że układ zamknięty w stanie stabilności po wytrąceniu ze stanu równowagi dynamicznej wraca do stanu równowagi samorzutnie, natomiast układ zamknięty będący w stanie niestabilnym wytrącony ze stanu początkowego już do niego nie wraca, ale oddala się od niego coraz bardziej.

Jeśli części rzeczywiste pierwiastków równania, leżą po lewej stronie osi Img to układ jest stabilny, natomiast po prawej stronie zachowuje się niestabilnie co można zauważyć na 1 i 2 wykresie.

Głównym celem ćwiczenia było zapoznanie się z podstawowymi rodzajami układów dynamicznych, serwomechanizmów i sposobem badania ich stabilności.

- 8 -

---