Uniwersytet Warmińsko-Mazurski w Olsztynie

Wydział Geodezji i Gospodarki Przestrzennej

Ćwiczenie 22

Wyznaczenie współczynnika załamania

oraz kąta granicznego ciał stałych

Jarosław Wróblewski

Wojciech Piotrowiak

Marcin Wąsowicz

Dualizm korpuskularno - falowy światła polega na tym, że niektóre zjawiska dają się wytłumaczyć zarówno na podstawie teorii falowej, jak i kwantowej, inne tłumaczą się tylko falowo lub tylko korpuskularnie.

Twórcą teorii korpuskularnej był Newton. Według niego światło polega na ruchu bardzo drobnych cząstek - korpuskuł. W określonym ośrodku posiadają one ustaloną prędkość i pęd.

Twórcą teorii falowej światła, był Huygens. W późniejszym okresie poprawki i uzupełnienia do teorii Huygensa wnieśli m.in. tacy badacze jak Fresnel, Young, Fraunhofer. Według teorii falowej światło jest falą elektromagnetyczną. Istota fali elektromagnetycznej polega na rozchodzeniu się drgań wektora natężenia pola elektrycznego i sprzężonego z nim wektora indukcji pola magnetycznego, prostopadłych względem siebie i względem rozchodzenia się fali, a więc jest falą poprzeczną.

Na rzecz teorii korpuskularnej przemawia prawo odbicia, zjawisko fotoelektryczne, zjawisko Comptona oraz pochłanianie i emisja promieniowania.

Prawem odbicia rządzą dwa podstawowe prawa, a mianowicie: 1) kąt padania  i kąt odbicia  leżą w jednej płaszczyźnie; 2) kąt padania  równa się kątowi odbicia 

Zjawisko Comptona przedstawia schematycznie rysunek

Kwant promieniowania hv (foton rentgenowski) pada wzdłuż osi x na spoczywający elektron. W wyniku sprężystego zderzenia elektron odrzucony zostaje z prędkością v pod kątem  względem osi x, a równocześnie tor fotonu odchyla się o kąt  w przeciwną stronę. Foton oddaje przy zderzeniu część swej energii, a więc po zderzeniu ma mniejszą częstotliwość v', a dłuższą falę. Przy zderzeniu sprężystym obowiązuje zasada zachowania energii i pędu. Jednak zjawisko Comptona zachodzi wyraźnie tylko wtedy, gdy padające promienie mają dużą częstotliwość i tylko w przypadku zderzeń fotonów z elektronami słabo związanymi z atomami, gdyż jedynie wtedy można je uważać za swobodne.

Za teorią falową przemawia natomiast prawo załamania, interferencja, dyfrakcja i polaryzacja.

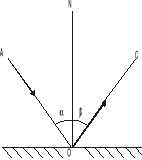
Załamanie światła na granicy dwóch ośrodków podlega następującym prawom: 1) kąt padania  i kąt załamania  leżą w jednej płaszczyźnie, kąt załamania jest to kąt utworzony przez normalną ON' i promień załamany OB; 2) stosunek sinusa kąta padania do sinusa kąta załamania równa się stosunkowi prędkości v₁ rozchodzenia się światła w ośrodku pierwszym do prędkości v₂ rozchodzenia się światła w ośrodku drugim. Jest to wielkość stała dla danych dwóch ośrodków i danego rodzaju promieniowania

Wielkość n_2/1 nazywamy współczynnikiem załamania ośrodka drugiego względem pierwszego. Natomiast bezwzględnym współczynnikiem załamania jest współczynnik załamania danego ośrodka względem próżni.

Interferencja światłą - nakładanie się spójnych wiązek światła. Zjawisko interferencji światła występuje wtedy, gdy w określonym punkcie przestrzeni nakładają się dwie jednakowe, monochromatyczne fale świetlne (czyli o jednakowej częstotliwości). Fale te wzmacniają się lub osłabiają, zależnie od różnicy faz w miejscu spotkania. Najsilniejsze wzmocnienie towarzyszy nakładaniu się fal w fazach zgodnych, najsilniejsze osłabienie - nakładaniu się fal w fazach przeciwnych.

Dyfrakcja światła - ugięcie fal świetlnych. Światło przechodząc przez jakikolwiek otwór o skończonych wymiarach rozchodzi się w dalszym ciągu tak, jak gdyby każdy punkty w obrębie tego otworu był osobnym źródłem nowego ruchu falowego (zasada Huygensa). W rezultacie promienie świetlne po przejściu przez otwór biegną nie tylko w kierunku swego poprzedniego ruchu lecz rozchodzą się na boki, czyli uginają się. Im mniejszy otwór tym ugięcie większe.

Polaryzacja polega na uporządkowanym drganiu wektorów natężenia pola elektrycznego (E) i magnetycznego (H). Światło rozchodzące się bezpośrednio od źródła, choćby miało najmniejsze rozmiary wysyła światło niespolaryzowane, tzn. w promieniowaniu biegnącym w kierunku k bezpośrednio od źródła, występują zmiany wektora świetlnego we wszystkich kierunkach prostopadłych do wektora k. Jeżeli zmiany wektora E we wszystkich falach składowych sprowadzimy do jednej płaszczyzny, zawierającej wektor k, mamy do czynienia ze światłem liniowo spolaryzowanym. Płaszczyzna przechodząca przez wypadkowy wektor E i k nosi nawę płaszczyzny drgań wektora świetlnego. Płaszczyznę do niej prostopadłą (zawierającą wektor H i k) nazywamy - według umowy przyjętej w optyce - płaszczyzną polaryzacji.

Prawo odbicia i załamania można udowodnić opierając się na zasadzie Fermata sformułowanej w XVII wieku. Zgodnie z tą zasadą promień świetlny biegnie od dowolnego punktu A do innego punktu B taką drogą, by czas potrzebny na jej przebycie był ekstremalny, tzn. najkrótszy lub najdłuższy z możliwych.

Zjawisko całkowitego wewnętrznego odbicia następuje wtedy, kiedy są spełnione następujące warunki: 1) promień przechodzi z ośrodka o mniejszej prędkości rozchodzenia się światła (czyli z ośrodka optycznie gęstszego) do ośrodka o prędkości większej (optycznie rzadszego); 2) kąt padania promienia musi być większy od tzw. kata granicznego. Przez kąt graniczny rozumiemy taki kąt padania, któremu odpowiada kąt załamania równy 90°.

Ćwiczenie - obliczenia

Płytka płasko - równoległa ze szkła

Pomiar
1	30 ^o	20 ^o	1,5311	1,5021
2	59 ^o	36 ^o	1,5062
3	52 ^o	33 ^o	1,5040
4	57 ^o	35 ^o	1,5329
5	45 ^o	25 ^o	1,5022
6	30 ^o	20 ^o	1,5311
7	50 ^o	30 ^o	1,5022
8	56 ^o	33 ^o	1,5085
9	38 ^o	24 ^o	1,5845
10	20 ^o	14 ^o	1,3801
11	61 ^o	35 ^o	1,5311
12	53 ^o	31 ^o	1,4966

Dyskusja błędów:

Obliczamy błąd bezwzględny poszczególnych funkcji n = f (,) obliczamy jako różniczkę zupełną tej funkcji i przyjmujemy wartości bezwzględne wszystkich składników wyrażenia

Błąd bezwzględny:

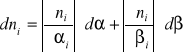
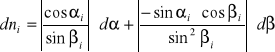
Średnia wartość błędu:

n = 1,50
0,08

Błąd względny:

Płytka płasko - równoległa z pleksi

Pomiar
1	46 ^o	29 ^o	1,5083	1,4822
2	63 ^o	37 ^o	1,4805
3	56 ^o	34 ^o	1,4826
4	23 ^o	15 ^o	1,5097
5	64 ^o	38 ^o	1,4599
6	38^o	23 ^o	1,5757
7	61 ^o	37 ^o	1,4533
8	34 ^o	23 ^o	1,4311
9	73 ^o	44 ^o	1,3766
10	33 ^o	22 ^o	1,4539
11	50 ^o	32 ^o	1,4456
12	60 ^o	38 ^o	1,4390

Dyskusja błędów:

Obliczamy błąd bezwzględny poszczególnych funkcji n = f (,) obliczamy jako różniczkę zupełną tej funkcji i przyjmujemy wartości bezwzględne wszystkich składników wyrażenia

Błąd bezwzględny:

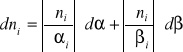
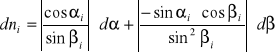
Średnia wartość błędu:

n = 1,48
0,07

Błąd względny:

Współczynnik załamania światła przy znanym kącie granicznym

Półkrążek ze szkła

Pomiar
1	41 ^o	1,5243	1,5093
2	42 ^o	1,4945
3	43 ^o	1,4663
4	41 ^o	1,5243
5	42 ^o	1,4945
6	42^o	1,4945
7	42 ^o	1,4945
8	41 ^o	1,5243

Dyskusja błędów:

Błąd bezwzględny:

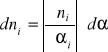
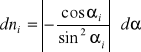
Średnia wartość błędu:

n = 1,51
0,03

Błąd względny:

Półkrążek z pleksi

Pomiar
1	41 ^o	1,5243	1,5244
2	41 ^o	1,5243
3	40 ^o	1,5557
4	41 ^o	1,5243
5	42 ^o	1,4945
6	42^o	1,4945
7	41 ^o	1,5243
8	40 ^o	1,5557

Dyskusja błędów:

Błąd bezwzględny:

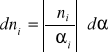
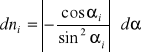
Średnia wartość błędu:

n = 1,52
0,03

Błąd względny:

---