P09

Edyta Dorsz

Marek Cichon

Sprawozdanie z zajęć laboratoryjnych

Ćwiczenie 8 :Miernictwo elektryczne wielkości nieelektrycznych

1.Cel ćwiczenia

Celem ćwiczenia jest wyznaczenie charakterystyki oporu w funkcji temperatury. Do pomiarów temperatury wykorzystano termistor i termometr platynowy, dla których mierzono zmiany oporności obu czujników przy wzroście temperatury i wyznaczenie zależności między opornością poszczególnych termometrów a temperaturą.

2.Wyniki uzyskane podczas badania wpływu temperatury na oporność czujnika platynowego i oporność termistora:

t [0C]	T[ K]	Rtermistora [k ]	RPt [ ]
33,6	306,75	74,98	565,8
36,8	309,95	63,86	572,4
41,7	314,85	52,95	581
46,2	319,35	44,72	589,1
50,3	323,45	37,78	597,8
54,9	328,05	31,14	608
60,4	333,55	26,46	617,1

3. Termometr oporowy platynowy

Termometr platynowy może być stosowany w szerokim zakresie temperatur (od - 259 ᵒC do 961ᵒC). Znajduje on zastosowanie w pomiarach wielu procesów ze względu na fakt, że platyna, jako metal szlachetny, jest odporna na korozję oraz ze względu na jej większy opór właściwy w porównaniu z innymi metalami.

Najczęstszym rozwiązaniem jest czujnik wykonany z drutu nawiniętego bifilarnie na izolatorze. Zależność oporności platyny od temperatury ma charakter prostoliniowy . Dla dokładniejszego opisu zależności rezystancji czujnika od temperatury stosuje się jej przybliżenie wielomianowe:

R=A+BT+CT²+…

Czynnikiem mającym wpływ na uzyskane wyniki jest oporność przewodów oraz ciepło jakie zostało wydzielone spowodowane przepływem prądu pomiarowego.

Równanie prostej : y =1,930x + 500,8

Szybkość zmian oporności względem temperatury dR/dT równa jest wartości współczynnika A i wynosi 1,930 Ω/˚C.

R₀-oporność w temperaturze 0˚C równa jest wartości współczynnika B równania prostej i wynosi 500,8 Ω.

Korzystając z powyższych wielkości można obliczyć współczynnik α dla czujnika platynowego:

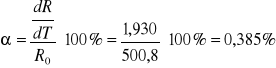
Porównanie współczynnika  z wartością literaturową:

Wartość literaturowa współczynnika  wynosi 0,385 %

Błąd względny:

0,385% - 0,385 % = 0,000%

Błąd bezwzględny:

0,000%/ 0,385%=0,000%

4. Termistor

Równanie prostej: lnR = 3989(1/T) - 8,701

Szybkość zmiany logarytmu naturalnego oporności względem odwrotności temperatury:

A=d lnR/d[1/T]= 3989 [k*K]

Logarytm naturalny z wartości granicznej, do której zmierza oporność, gdy temperatura dąży do nieskończoności:

B = -8,701 [k
]

Wartości współczynnika
termistora wyznaczamy z wzoru:

Dla T = 306,75 K

= [3989/(306,75)^2]*100% = -4,25%/K

Dla T = 309,95

= [3989/(309,95)^2]*100% = -4,15%/K

Dla T = 314,85

= [3989/(314,85)^2]*100% = -4,02%/K

Dla T = 319,35

= [3989/(319,35)^2]*100% = -3,91%/K

Dla T = 323,45

= [3989/(323,45)^2]*100% = -3,81%/K

Dla T = 328,05

= [3989/(328,05)^2]*100% = -3,7%/K

Dla T = 333,55

= [3989/(333,55)^2]*100% = -3,58%/K

5. Wahania temperatury w termistorze

5. Wnioski

Jedyną wadą termometrów platynowych jest ich cena, jednak tę wadę równoważą nam liczne zalety takie jak: szeroki zakres pomiaru, stabilny i niezawodny pomiar temperatury, dość dobra dokładność (ok. 0,1), duża precyzja.

Termistory są powszechnie w kalorymetrii i kriometrii, gdyż wyniki przez nie osiągane mają dokładność rzędu +/- 0,0001˚C, co ważne jest przy tego typu pomiarach.

---