GRUPA 4A |
||
Pomiary częstotliwości i fazy
|
|
|
|
Data wykonania ćwiczenia |
26.04.2005 |
|
Data odbioru sprawozdania |
04.05.2005 |
|
Ocena zaliczenia |
|
|
|
|
Sprawozdanie
9.5.1. Pomiar częstotliwości metodą pomiaru okresu
Do wyznaczenia wartości częstotliwości z pomiaru okresu posługujemy się wzorem:
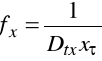
Dtx = 0.05ms/cm - podstawa czasu
x = 9.95cm - długość jednego okresu przebiegu na ekranie oscyloskopu
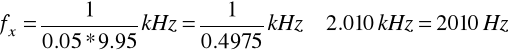
Natomiast do wyznaczenia błędu systematycznego pomiaru częstotliwości metodą różniczki zupełnej posługujemy się poniższymi wzorami:
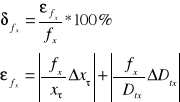
Po podstawieniu wzoru na częstotliwość otrzymujemy:
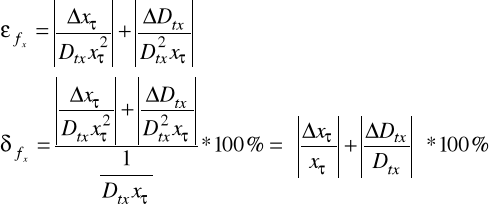
x = 1mm - błąd odczytu z ekranu oscyloskopu
Dtx /Dtx = 3% - błąd generatora podstawy czasu
![]()
Tablica 9.1
Metoda bezpośrednia:
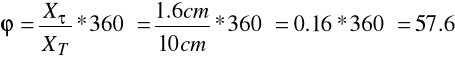
Tablica 9.2
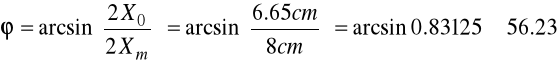
Tablica 9.5
Tablica 9.8
KZ-1508
XT [cm] |
9.95 |
Dtx [ms/cm] |
0.05 |
fx [Hz] |
2010 |
δfx [%] |
4 |
9.5.2. Pomiar częstotliwości metodą figur Lissajous
f1 = 200Hz ,
f2 = 600Hz .
9.5.3. Pomiary przesunięcia fazowego
Obliczenie teoretycznej wartości przesunięcia fazowego:
R = 1k
C = 244nF
f = 1kHz
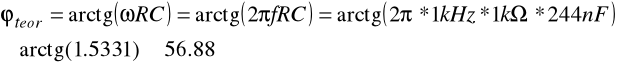
X = 1.6cm - długość odcinka proporcjonalnego do kąta przesunięcia fazowego
XT = 10cm - długość jednego okresu przebiegu na ekranie oscyloskopu
X, XT = 1mm - błąd odczytu z ekranu oscyloskopu
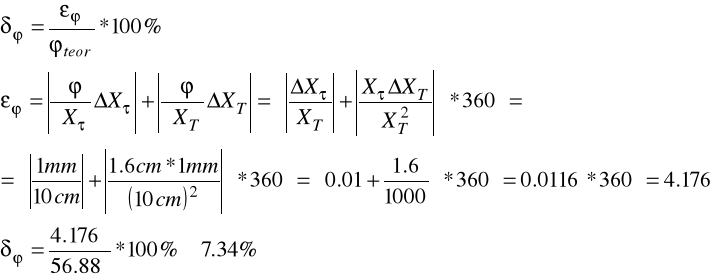
XT [cm] |
10 |
X [cm] |
1.6 |
[] |
57.6 |
δ [%] |
7.34 |
![]()
Zmierzony kąt mieści się w granicach błędu.
Metoda figur Lissajous:
2X0 = 6.65cm
2Xm = 8cm
X, XT = 1mm - błąd odczytu z ekranu oscyloskopu
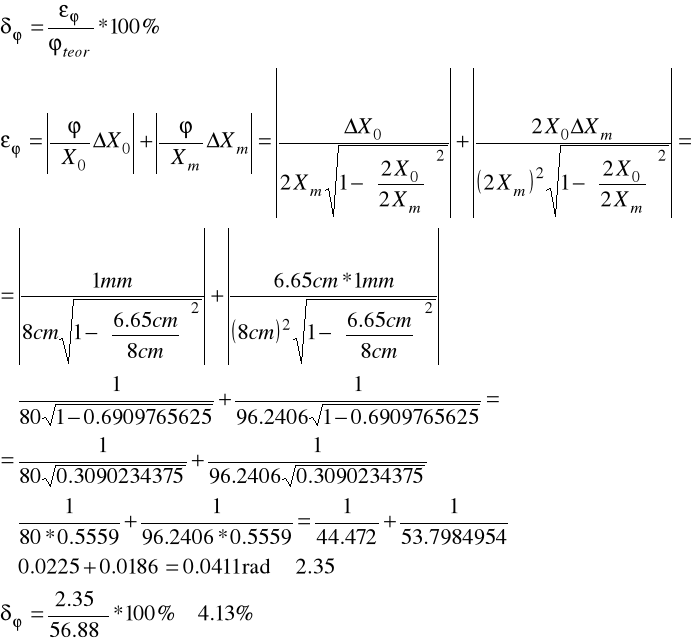
Tablica 9.3
2Xm [cm] |
8 |
2X0 [cm] |
6.65 |
[] |
56.23 |
δ [%] |
4.13 |
![]()
Zmierzony kąt mieści się w granicach błędu.
9.5.4. Badanie metody cyfrowego pomiaru częstotliwości
Częstotliwość wyznaczamy ze wzoru:
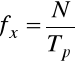
Błąd dyskretyzacji obliczamy ze wzoru:
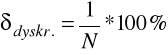
Tp [s] |
0,001 |
0,01 |
0,1 |
1 |
10 |
100 |
20 |
N |
5 |
50 |
500 |
5000 |
49999 |
499991 |
99998 |
fx [Hz] |
5000 |
5000 |
5000 |
5000 |
4999.9 |
4999.91 |
4999.9 |
δdyskr. [%] |
20 |
2 |
0.2 |
0.02 |
0.002 |
0.0002 |
0.001 |
9.5.5. Cyfrowy pomiar stabilności częstotliwości drgań generatorów
|
HM 8032 |
|||
fśr [Hz] |
4995.788521 |
5000.147550 |
||
std dev [Hz] |
0.004282 |
0.000016 |
||
fmax [Hz] |
4995.79707 |
5000.14759 |
||
fmin [Hz] |
4995.78017 |
5000.14752 |
||
fnom [Hz] |
5000 |
5000 |
||
f [Hz] |
0.01690 |
0.00007 |
||
f / fnom [%] |
0.000338 |
0.0000014 |
||
Wniosek:
Generator KZ-1508 wykazuje lepszą stabilność, gdyż posiada on kwarcowy wzorzec częstotliwości. W generatorze HM 8032 wykorzystany został mostek Wiena, którego działanie jest bardziej uzależnione od warunków zewnętrznych.
9.5.6. Obserwacja przebiegów cykloidalnych
Epicykloida
f1 = 600Hz ,
f2 = 1800Hz ,
Hipocykloida
f1 = 600Hz ,
f2 = 1800Hz ,
Strona 6
1V/cm
1V/cm
Tryb: XY
1V/cm
1V/cm
Tryb: XY
0.5V/cm
0.5V/cm
Tryb: XY
0.5V/cm
0.5V/cm
Tryb: XY
Wyszukiwarka