IX/X. Genetyka populacji

- Równowaga Hardy'ego-Weinberga,

- szacowanie częstości alleli i genotypów,

IX/X. Genetyka populacji

Genetyka populacji zajmuje się rozkładem (dziedziczeniem) genów w populacjach i bada zmienność rozkładu częstości (frekwencji) genów, genotypów i fenotypów w czasie.

Pula genowa to zbiór wszystkich alleli w danej populacji.

Populacja jest to zbiór roślin czy też zwierząt określonego gatunku.

Bardziej precyzyjna jest definicja populacji genetycznej.

Populacja genetyczna (mendlowska) jest to zbiór osobników jednego gatunku, zasiedlających wspólny obszar, krzyżujących się ze sobą w sposób losowy, bez żadnych ograniczeń. Taki sposób krzyżowania nosi nazwę panmiksji (lub krzyżowania panmiktycznego) i prowadzi do losowej wymiany alleli (chromosomów) w obrębie wspólnej puli genów. Prawdopodobieństwo kojarzenia się ze wszystkimi osobnikami płci przeciwnej jest jednakowe.

Ta definicja populacji odnosi się do organizmów rozmnażających się płciowo w sposób swobodny, czyli na przykład: ludzi, zwierząt, roślin obcopylnych. Nie dotyczy natomiast roślin samopylnych, u których preferowane jest zapylenie i zapłodnienie własnym pyłkiem, i roślin rozmnażających się wegetatywnie, przez co powstają klony - organizmy o identycznym genotypie.

Wyróżnia się populacje naturalne i sztuczne, stworzone przez człowieka w procesie hodowli roślin lub zwierząt.

Swobodne krzyżowanie osobników w ramach pewnej puli genowej powoduje określone konsekwencje genetyczne.

Podstawowym pojęciem genetyki populacji jest częstość genu, która oznacza stosunek liczby alleli określonego rodzaju do wszystkich alleli w danym locus w populacji.

Suma częstości alleli z tego samego locus równa się 1 czyli 100% - przedstawia to wzór:

p + q = l (100%), czyli q = 1 - p; gdzie ρ - częstość allelu A,

q - częstość allelu a.

Stosunek między frekwencją genów a frekwencją genotypów w obrębie populacji określa prawo Hardy'ego-Weinberga. Prawo Hardy'ego-Weinberga, sformułowane niezależnie przez obu uczonych w latach 1908-1909, brzmi:

W dostatecznie licznej, zrównoważonej populacji panmiktycznej, częstości alleli i genotypów

nie zmieniają się w kolejnych pokoleniach, o ile nie zachodzą w niej mutacje, migracje,

selekcja, dobór par do kojarzenia i dryf genetyczny.

Ponieważ potomstwo powstaje z połączenia gamety żeńskiej i męskiej, które zawierają jeden z dwóch alleli, częstości genotypów odpowiadają poszczególnym składnikom rozwiniętego dwumianu:

♀ (p + q) x ♂ (p + q) = (p + q)² = p² + 2pq + q² = l , gdzie p² - frekwencja genotypu AA,

2pq - frekwencja genotypu Aa,

q² - frekwencja genotypu aa.

Ponieważ:

- homozygoty dominujące powstają po połączeniu gamety męskiej niosącej allel A (częstość p) i gamety żeńskiej niosącej allel A (częstość p), więc częstość genotypu AA równa się ρ x p = p²,

- heterozygoty powstają po połączeniu gamety męskiej niosącej allel A (częstość p) i gamety żeńskiej niosącej allel a (częstość q), czyli częstość takiego zjawiska równa się ρ x q = pq i sytuacja odwrotna połączenie męskiego

allelu a i żeńskiego allelu A p x q = pq, zatem całkowita częstość heterozygot Aa równa się pq + pq = 2pq,

- homozygoty recesywne powstają po połączeniu gamety męskiej niosącej allel a (częstość q) i gamety żeńskiej niosącej allel a (częstość q), więc częstość genotypu aa równa się q x q = q².

Uwaga!

Prawdopodobieństwo jednoczesnego wystąpienia zjawisk niezależnych jest iloczynem ich prawdopodobieństw. Prawdopodobieństwo wystąpienia zjawisk wykluczających się jest sumą ich prawdopodobieństw.

Inaczej zapisując - udział w populacji poszczególnych genotypów wynosi:

gamety	A(p)	a(q)
A(p)	AA(p^2)	Aa (pq)
a(q)	Aa (pq)	aa (q^2)

Przykład 1

a. W przypadku kiedy udział obu alleli w populacji jest jednakowy (p = 0,5, q = 0,5), otrzymujemy następujące frekwencje genotypów:

AA - 0,5² = 0,25

Aa - 2 (0,5 x 0,5) = 0,5

aa - 0,5² = 0,25

Homozygoty dominujące, heterozygoty i homozygoty recesywne występują wówczas w populacji w stosunku liczbowym 1:2:1.

b. Jeśli jeden allel znacznie przeważa częstością występowania nad drugim (p = 0,8, q = 0,2), genotypy występują z następującą częstością:

AA - 0,8² = 0,64

Aa - 2 (0,8 x 0,2) = 0,32

aa - 0,2² = 0,04

c. Jeśli występuje tylko jeden allel danego genu (np. A), wówczas ρ = 1, q = 0. Otrzymujemy następujące frekwencje genotypów:

AA- 1² = 1

Aa - 2 (1 x 0) = 0

aa - 0² = 0

W takiej populacji, zgodnie z przewidywaniami, wszystkie osobniki są homozygotami AA.

Równowaga Hardy'ego-Weinberga jest stabilna z pokolenia na pokolenie, jeśli brak jest czynników zakłócających. Czynniki zaburzające stan równowagi to:

1. Mutacje genowe i chromosomowe powodujące powstawanie organizmów o nowych genotypach. Tworzą się wówczas nowe geny lub powstaje nowe rozmieszczenie genów na chromosomie. Jeśli mutanty mają korzystniejsze właściwości adaptacyjne, to udział genotypów zawierających zmutowany gen będzie wzrastał w kolejnych pokoleniach, aż równowaga Hardy'ego-Weinberga ustali się na nowym poziomie. Powstaną również nowe sprzężenia genów.

2. Selekcja

• naturalna - zachodząca w sposób naturalny, preferująca organizmy lepiej przystosowane do warunków środowiska. Jeśli zmienią się warunki, to może się okazać, że pewne genotypy lepiej je znoszą niż pozostałe. Taka sytuacja spowoduje wzrost frekwencji alleli korzystniejszych w zmienionym środowisku. Na przykład ćmy Biston betularia spędzające dzień na pniach brzóz, w rejonach silnie uprzemysłowionych częściej występują jako formy o ciemnych skrzydłach, podczas gdy w XIX wieku 99% populacji miało skrzydła jasne;

• sztuczna - prowadzona w sposób celowy przez człowieka podczas hodowli roślin lub zwierząt. Hodowca wybiera do dalszego krzyżowania formy o korzystnych cechach (np. krótkim źdźble), odrzucając pozostałe. W ten sposób frekwencja alleli warunkujących te właściwości wzrasta z pokolenia na pokolenie. Z kolei cechy niekorzystne z punktu widzenia człowieka (utrudniające uprawę lub wykorzystanie surowców roślinnych) w miarę możliwości są eliminowane z populacji.

3. Migracje, czyli odrywanie się grupy osobników od głównej populacji i często ich całkowita izolacja. Migrująca grupa może mieć inny skład genów niż populacja wyjściowa (rys. 1). Na przykład w przypadku ludzi mogą to być osobnicy szczególnie przedsiębiorczy i odważni albo też w przypadku zesłania karnego -kryminaliści. Odległe geograficznie populacje ludzi czy zwierząt często mają zupełnie inny udział poszczególnych genotypów i fenotypów (np. allele kodujące grupy krwi). Swobodne podróżowanie i osiedlanie się ludzi czy zawleczenie żywych zwierząt lub roślin z innych rejonów świata powoduje zmianę równowagi Hardy'ego-Weinberga na danym terenie. Po pewnym czasie równowaga ta ustala się na innym, nowym poziomie.

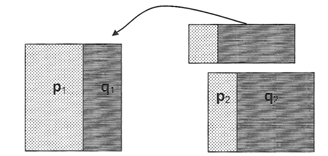
Rysunek 1. Zmiana frekwencji alleli w populacji pod wpływem migracji

4. Dryf genetyczny (zwany też dryftem genetycznym) jest to nagła, niedająca się przewidzieć zmiana udziału genotypów w populacji na skutek gwałtownego obniżenia jej liczebności (np. w wyniku katastrofy żywiołowej). Frekwencja alleli wśród nielicznych, ocalałych osobników może przypadkowo być zupełnie inna niż w populacji wyjściowej. Szczególnie wrażliwe na dryf genetyczny są małe populacje, na przykład powstałe na skutek migracji. Przykładem są żółwie zamieszkujące poszczególne wyspy archipelagu Galapagos, które mają różnie urzeźbione skorupy. Prawdopodobnie podczas powstawania archipelagu, w dramatycznych okolicznościach, doszło do rozpadu pierwotnej populacji i izolacji niewielkich grup żółwi o różnej frekwencji alleli.

5. Preferencyjne (nielosowe) krzyżowanie powoduje zakłócenia równowagi Hardy'ego-Weinberga. Warunkiem zachowania równowagi jest panmiksja, krzyżowanie całkowicie losowe. Jeśli na przykład kwiaty o określonej barwie są częściej odwiedzane przez pszczoły lub pewne fenotypy są preferowane podczas łączenia się w pary osobników (np. samce robaczka świętojańskiego świecące na niebiesko, kobiety o blond włosach), to wzrasta frekwencja tych alleli w kolejnych pokoleniach.

Przykład 2

Albinotyzm u ludzi warunkowany jest recesywnym genem w stanie homozygotycznym, homozygoty dominujące i heterozygoty nie wykazują objawów albinotyzmu. Częstość występowania albinosów wynosi jeden przypadek na 10 000 osobników.

***

To oznacza, że częstość genotypu recesywnego q² = 1: 10 000. Zatem częstość allelu recesywnego wynosi:

częstość allelu dominującego ρ wynosi więc ρ = 1 - 0,01 = 0,99. Oznacza to, że przeciętnie na 100 gamet można spodziewać się jednej niosącej allel recesywny i 99 z allelem dominującym.

Ustalona na podstawie częstości fenotypów częstość obu alleli pozwala na ustalenie częstości genotypów w populacji przez podstawienie częstości alleli do wzoru Hardy—Weinberga:

W populacji ludzi można zatem oczekiwać, że na 10 000 osobników jeden jest homozygotą recesywną, 198 - heterozygotami i 9801 - homozygotami dominującymi.

Przykład 3

Znana jest seria alleli wielokrotnych L^A, L^B i warunkujących grupy krwi systemu AB0. Obecność trzech alleli tej serii umożliwia powstanie 6 różnych genotypów i 4 różnych fenotypów (grup krwi):

***

Uwzględniając możliwość tworzenia różnych genotypów przy trzech allelach po rozszerzeniu wzoru Hardy -Weinberga do postaci:

można ustalić prawdopodobną częstość genotypów i fenotypów w populacji. Częstość ta będzie następująca:

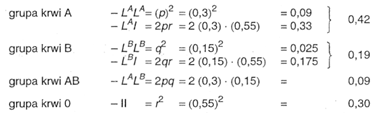
Prawdopodobna częstość fenotypów z poszczególnymi grupami krwi wynosi: 42% ludzi z grupą krwi A, 19% z grupą krwi B, 9% - z grupą AB i 30% z grupą krwi 0.

Przykład 4

Rozpatrując dwa niezależne geny: gen warunkujący grupę krwi 0 i gen warunkujący czynnik Rh, można ustalić częstość występowania ludzi, u których obie cechy są obecne łącznie. Jak wiadomo, grupę krwi 0 warunkuje gen w stanie homozygotycznym ii, częstość homozygot wynosi 0,3. Czynnik Rh^- warunkowany jest genem w stanie

homozygotycznym dd (homozygoty dominujące DD i heterozygoty Dd mają czynnik Rh⁺). Częstość homozygot dd wynosi 0,16.

***

Częstość fenotypów, u których wystąpią łącznie obie cechy: grupa krwi 0 i Rh^-, będzie iloczynem częstości homozygot recesywnych obu genów, czyli (0,3) x (0,16) = 0,048. Można więc spodziewać się 4,8% ludzi, u których obie cechy wystąpią łącznie.

Przykład 5

Fenyloketonuria jest rzadkim schorzeniem polegającym na nieprawidłowej przemianie aminokwasów aromatycznych. Jeden chory przypada na 25 tysięcy osób. Jaka jest częstotliwość występowania w populacji nosicieli?

***

Chory - homozygota recesywna aa; Nosiciel - heterozygota Aa

Zgodnie z prawem Hardy'ego-Weinberga częstotliwość występowania homozygot recesywnych w populacji wynosi q² = 1/25000.

Wobec tego częstość allelu a: q = 1/158.

Częstość allelu prawidłowego A: ρ = 1 - q= 157/158.

Heterozygoty występują z częstotliwością 2pq = 2(1/158 x 157/158) = 2(157/25000) = 314/25000.

Tak więc na populację liczącą 25 tysięcy osób przypada średnio jedna osoba chora i 314 nosicieli allelu fenyloketonurii.

Przykład 6

Na łące znajdują się rośliny pewnego gatunku o kwiatach niebieskich - allel dominujący B i różowych - allel recesywny b. Oba allele początkowo występują w takich samych proporcjach. Na skutek katastrofalnej powodzi ginie większość roślin. Wśród ocalałych osobników przypadkowo 5 ma kwiaty różowe, 2 zaś - niebieskie (jeden jest homozygota, a drugi heterozygota). Na jakim poziomie ustali się równowaga w następnych pokoleniach? Jaka będzie frekwencja poszczególnych genotypów i fenotypów?

***

W ocalałej populacji występuje: 5 x bb, 1 x BB i 1 x Bb, tak więc 11 razy pojawia się allel b i tylko 3 razy B. Częstość allelu Β: ρ = 3/14 = 0,21, allelu b zaś: q = 1 - p = 0,79.

W następnych pokoleniach (przy założeniu losowego krzyżowania, braku selekcji, jednakowej płodności itd.):

• homozygoty BB będą występować z częstotliwością p² = 0,044;

• heterozygoty Bb będą występować z częstotliwością 2pq = 0,332;

• homozygoty bb będą występować z częstotliwością q² = 0,624.

Czyli przeciętnie w populacji występuje 4,4% homozygot BB, 33,2% heterozygot Bb i 62,4% homozygot bb, fenotypowo zaś - 37,6% roślin o kwiatach niebieskich i 62,4% roślin o kwiatach różowych.

Pytania sprawdzające:

1………………….to zespół osobników, które mogą swobodnie krzyżować się między sobą i zamieszkują na określonym terenie.

2. Gdy wszystkie osobniki płci………….mogą krzyżować się ze sobą z jednakowym prawdopodobieństwem, to mówimy o…………….

2. Prawo Hardy'ego-Weinberga odnosi się do populacji……………….., zgodnie z nim populacja osiągnie stan……………….po jednym pokoleniu losowego krzyżowania.

4. Częstość allelu dominującego oznaczamy……….., recesywnego zaś…………….., suma ρ + q równa się………… Rozkład genotypów w populacji odpowiada rozkładowi czynników rozwiniętego dwumianu……….=………..

5. Jeśli w losowo krzyżującym się stadzie liczącym 1000 osobników częstość allelu recesywnego q wynosi 0,4, to możemy oczekiwać………….osobników o fenotypie recesywnym i…………o fenotypie dominującym (w przypadku pełnej dominacji genu).

6. W przypadku choroby autosomalnej recesywnej występującej z częstością 1/10 000 częstość heterozygot w populacji wynosi…………..

7. W grupie 10 000 ludzi cecha recesywna sprzężona z chromosomem X pojawi się u………..kobiet i………mężczyzn, jeśli q = 0,03.

Zadania do samodzielnego rozwiązania:

1. W czystej rasie bydła Holstein jedno cielę na 100 rodzi się łaciate, co warunkowane jest recesywnym genem. Ustalić frekwencję genu warunkującego łaciatość oraz frekwencję homozygot i heterozygot w populacji.

2. W populacji znajduje się 8% mężczyzn dotkniętych daltonizmem. Zakładając, że daltonizm nie zmniejsza żywotności osobników, jaki procent kobiet z daltonizmem wystąpi w tej populacji? Daltonizm jest determinowany przez recesywny gen sprzężony z płcią.

3. W określonej populacji ludzkiej 99% osobników ma grupę krwi Rh+, co wiąże się z obecnością dominującego allelu D. Jaka będzie częstość genotypów Dd i DD, jeżeli krzyżowanie jest przypadkowe?

4. Łysienie warunkowane jest dominującym genem działającym wyłącznie u mężczyzn. Kobiety nie łysieją niezależnie od genotypu. Zakładając, że częstość genu łysienia = p, a małżeństwa dobierają się losowo, wykazać:

1. częstość łysych synów w seriach rodzin, gdzie ojciec nie łysieje,

2. częstość niełysiejących synów w seriach rodzin, w których ojciec łysieje.

Kolejne zadania z frekwencji genów i genotypów:

1. W pewnej populacji osobników stwierdzono, że frekwencje genotypów (przy rozpatrywaniu cechy uwarunkowanej jedną parą genów) wynoszą odpowiednio: AA - 0,2; Aa - 0,7; aa - 0,1.

a) Oblicz częstości genów (p_A i q_a) warunkujących tę cechę.

b) Sprawdź czy dana populacja jest w stanie równowagi genetycznej, a w przypadku stwierdzenia, że nie, podaj (z uzasadnieniem) kiedy stan równowagi może osiągnąć.

2. Częstość recesywnego allelu dla niezdolności do podłużnego zwijania języka oceniono na q = 0,6. Jakie są częstości osobników zdolnych i niezdolnych do zwijania języka?

3. Na wyizolowanym polu kukurydzy stwierdzono występowanie roślin o dwóch typach bielma: żółtym i białym. Za żółtą barwę odpowiada gen dominujący (A), natomiast za białą jego recesywny allel (a). W losowo zebranej z tego pola próbce 1000 nasion, 910 miało bielmo żółte. Ustalić frekwencję alleli A i a w tej populacji kukurydzy.

4. Bydło rasy shorthorn o genotypie C^RC^R ma umaszczenie czerwone, C^RC^W- dereszowate (czerwono-białe), a C^WC^W- białe.

a) W pewnym stadzie stwierdzono 108 osobników czerwonych, 48 białych i 144 osobniki dereszowate. Oblicz frekwencję alleli C^R i C^W.

b) Zakładając, że jest to populacja panmiktyczna, jakiej frekwencji zygot należałoby oczekiwać w następnym pokoleniu?

5. Kolor sierści kotów jest uwarunkowany parą równocennych genów. Osobniki żeńskie C^BC^B i męskie C^BY są czarne. Żeńskie C^YC^Y i męskie C^YY są żółte, natomiast żeńskie C^BC^Y są mozaikowate (żółto-biało-czarne).

W pewnej populacji kotów stwierdzono następujące liczebności różnych fenotypów:

ogółem czarne żółte mozaikowate

osobniki męskie 353 311 42 0

osobniki żeńskie 338 277 7 54

Ustalić frekwencję tych dwóch alleli w populacji.

6. U owiec biały kolor wełny jest uwarunkowany obecnością genu dominującego, podczas gdy czarny - allelem recesywnym. W stadzie liczącym 900 sztuk 891 miało wełnę białą, a 9 czarną. Wyliczyć frekwencję obydwu alleli w tym stadzie.

7. Gen (R) kontroluje u ludzi obecność antygenów występujących w czerwonych ciałkach krwi. Allel dominujący odpowiada za fenotyp Rh⁺, podczas gdy osobniki homozygotyczne recesywne mają Rh^-. W pewnej populacji stwierdzono 85% osobników z Rh⁺. Zakładając, że populacja jest w stanie równowagi, jaka jest frekwencja obydwu alleli?

8. W pewnej populacji ludzkiej 99% osób ma grupę krwi Rh+ (dominujący gen - R). Jaka będzie częstotliwość genotypów Dd i DD, jeżeli krzyżowanie jest przypadkowe?

9. Załóżmy, że analizujemy populację w której 16% osobników wykazuje ujemną reakcję Rh.

a) Jaka częstość alleli r lub R wypadnie z obliczenia, jeżeli przyjmiemy, że pod względem tego allelu populacja jest w równowadze przy losowym kojarzeniu się?

b) Oblicz rozkład genotypów w tej populacji.

10. Rozpoznawanie smaku fenylotiomocznika (PTC) jest dziedziczne i dominuje nad nierozpoznawaniem. Cecha jest determinowana przez parę alleli (T, t). W populacji znajduje się 70% osób odczuwających smak PTC. Jaka

jest częstość homozygot dominujących (TT) i heterozygot (Tt)?

11. Jeśli 24% populacji jest homozygotami odczuwającymi smak PTC, a 50% jest heterozygotami, jaka jest frekwencja recesywnego genu (t)?

12. Wśród ludności pochodzącej z południowych Włoch, mieszkającej obecnie w stanie New York, thalassemia major występuje u jednego noworodka na 2400, a thalassemia minor — u jednego na 25. Przy przeliczeniu

tych częstości na dziesięciotysięczną populację rozkład jest mniej więcej następujący:

Thalassemia major Thalassemia minor fenotyp normalny

ThTh Th+ ++

4 400 9 596

Przekonaj się, że w tej populacji częstość genu Th i jego normalnego allelu wynoszą odpowiednio około 0,02 i 0,98. Czy populacja ta ma w przybliżeniu dwumianowy rozkład genotypów, przewidywany na podstawie takiej częstości genów?

13. W populacji europejskiej częstość genu wrażliwości na PTC p_T = 0,45, a częstość q_t = 0,55. Jakie jest prawdopodobieństwo, że małżonkowie wrażliwi na PTC będę mieli dzieci niewrażliwe na ten związek chemiczny?

14. Oblicz na podstawie danych z zadania 13, prawdopodobieństwo urodzenia dzieci wrażliwych na PTC z małżeństwa „wrażliwy” x „niewrażliwy".

15. Indianie plemienia Hopi z zachodniej, górzystej i pustynnej części USA żyją w zamkniętych populacjach o wysokim stopniu krzyżowania krewniaczego. W populacji jest znacznie większy procent albinosów (1 :200) niż w Europie (1 :20 000). Jaki procent populacji Hopi stanowią heterozygoty?

16. W populacji soi składającej się z osobników o kolorze złocistożółtym, jasnozielonym i ciemnozielonym o genotypach odpowiednio C^GC^G, C^GC^D i C^DC^D stwierdzono: 2 rośliny złocistozielone, 35 roślin jasnozielonych i 162 rośliny ciemnozielone. Ustal frekwencję alleli C^G i C^D.

17. Jaką najwyższą frekwencję w populacji może osiągnąć gen recesywny, który w stanie homozygotycznym powoduje śmierć osobnika, u którego wystąpi? Jaki będzie wówczas skład genetyczny tej populacji?

18. Wśród 950 sztuk kóz rozmnażających się losowo znajduje się 798 bezrogich oraz 152 kóz rogatych. Bezrogość bądź rogatość wyznacza jedna para genów — (H) i (h), przy czym bezrogość jest cechą dominującą.

a) Ustal strukturę genetyczną przedstawionej populacji kóz.

b) Podaj, ile należy oczekiwać kóz bezrogich homo-, a ile heterozygotycznych?

19. Schwytano 2000 sztuk much Drosophila dziko żyjącej, a więc rozmnażającej się losowo. Większość z nich miała szarą barwę tułowia (gen dominujący b⁺), ale naliczono 45 sztuk czarnych (cecha uwarunkowana genem

recesywnym b).

a) Oblicz częstość występowania genu b⁺ i b (q_b i P_B).

b) Ustal ile należy oczekiwać w tej populacji much szarych homo-, a ile heterozygotycznych.

20. Skrzydlatość lub bezskrzydłość Drosophila zależy od pary genów vg⁺ i vg. (Osobniki o genotypach vg⁺vg⁺ i vg⁺vg są skrzydlate, o genotypach vgvg - bezskrzydłe). Do słoika z pożywką wpuszczono 485 much homozygotycznych skrzydlatych i 115 bezskrzydłych.

a) Czy tak utworzona populacja rodzicielska jest w równowadze genetycznej?

b) Podaj spodziewany rozkład genów, genotypów i fenotypów w pokoleniu F₁ otrzymanym przez losowe kojarzenie much opisanych w tym zadaniu.

c) Porównaj strukturę genetyczną w pokoleniu F₁ i w populacji rodzicielskiej.

21. Do słoika wpuszczono 120 much szarych homozygotycznych drozofili i 80 much czarnych. Muchom pozwolono rozmnażać się losowo.

a) Oblicz częstość genów wyznaczających barwę tułowia (p_S i q_s).

b) Czy otrzymana populacja rodzicielska jest w równowadze genetycznej?

c) Podaj oczekiwany rozkład genów, genotypów i fenotypów w pokoleniu F₁.

22. W populacji interesuje nas cecha, która uwarunkowana jest jedną parą genów - C, c. Zakupiono 100 osobników, wśród których było: 40 o genotypach CC, 40 - Cc oraz 20 - cc.

a) Oblicz frekwencję genów (p_C i q_c) i danych genotypów w zakupionej grupie osobników.

b) Sprawdź, czy ta grupa osobników jest zrównoważona genetycznie pod względem rozpatrywanej cechy.

23. Które z wymienionych populacji znajdują się w równowadze genetycznej:

AA Aa aa

1. 78 77 78

2. 126 - -

3. - 154 -

4. - - 137

5. 116 161 84

6. 81 126 49

24. Które z wymienionych populacji są w równowadze genetycznej?

a) 100% AA;

b) 100% aa;

c) 100% Aa;

d) 1% AA, 98% Aa, 1% aa;

e) 32% AA, 64% Aa, 4% aa;

f) 4% AA, 32% Aa, 64% aa.

25. W czterech różnych populacjach stwierdzono frekwencje genotypowe:

a) 26 000 AA : 18 000 Aa : 45 000 aa;

b) 49 AA : 42 Aa : 9 aa;

c) 0,4617 AA : 0,3221 Aa : 0,2162 aa;

d) 64/81 AA : 16/81 Aa : 1/81 aa.

Które z tych populacji są w stanie równowagi genetycznej, a które nie?

26. Jeżeli w zamkniętej populacji występuje recesywny allel z częstotliwością 0,2, a w drugiej równej liczebnie populacji allel ten nie występuje, to:

a) w jakiej części osobników pierwszej populacji allel ten ujawni się fenotypowo?

b) po złączeniu obu populacji w jedną i osiągnięciu stanu równowagi, jaka będzie częstotliwość recesywnej cechy?

27. W dwóch różnych populacjach częstości genów warunkujących tę samą cechę jakościową są jednakowe i wynoszą: p_B = 0,7; q_b= 0,3.

a) Zakładając, że jedna populacja osobników jest w równowadze genetycznej, a druga nie, podaj rozkłady genotypów w obydwu populacjach.

b) Po podaniu rozkładu genotypów w populacji niezrównoważonej ustal, kiedy może ona osiągnąć stan równowagi genetycznej.

28. W pewnej populacji przebadano 500 mężczyzn i stwierdzono, że 20 z nich było daltonistami.

a) Jaka jest frekwencja allelu dominującego w populacji?

b) Jaki procent kobiet w tej populacji nie cierpi na tę chorobę?

29. W populacji 8% mężczyzn jest daltonistami, zakładamy, że daltonizm nie zmniejsza żywotności osobników. Jaki procent kobiet z daltonizmem wystąpi w populacji?

30. Założenie: frekwencja genów wśród osobników męskich i żeńskich jest równa. W populacji europejskiej gen hemofilii występuje z częstością 0,03. Załóżmy, że w jednym województwie jest około 2 000 000 ludzi.

a) Oszacuj, ile osób może chorować na hemofilię.

b) Oszacuj, ile może być w tym województwie nosicieli genu h (osobniki zdrowe) i jakiej są płci.

31. Załóżmy, iż w pewnej populacji gen powodujący hemofilię występuje w 1% gamet.

a) Jakiej frekwencji osobników chorych na hemofilię możemy oczekiwać w tej populacji?

b) Jaka jest oczekiwana frekwencja kobiet chorych na hemofilię?

32. U muszki owocowej gen recesywny, sprzężony z płcią jest odpowiedzialny za biały kolor oczu (w). Jego allel dominujący w⁺ odpowiada za czerwoną barwę oczu (fenotyp dziki). W populacji wyhodowanej w warunkach laboratoryjnych analizowano kolor oczu u osobników męskich i stwierdzono, iż 170 miało oczy czerwone, a 30 oczy białe.

a) Ustalić frekwencję alleli w i w⁺.

b) Jaki procent osobników żeńskich w populacji będzie miał oczy białe?

33. Wśród białej ludności Ameryki Północnej ślepota na barwy występuje u prawie 8% mężczyzn, wśród Murzynów zaś - tylko u około 4% mężczyzn. Uwzględniając, że jest to cecha recesywna sprzężona z płcią, jakie

mógłbyś przewidzieć częstości występowania ślepoty na barwy u kobiet w każdej z tych populacji?

34. W pewnej populacji częstość kobiet wykazujących cechę nieszkodliwą, recesywna i sprzężoną z chromosomem X wynosi 1 na 10 000. Jaka jest częstość występowania mężczyzn wykazujących tę cechę?

35. W pewnej populacji 1% kobiet jest łysych.

a) Ile kobiet jest heterozygotami?

b) Ilu mężczyzn jest łysych?

36. Czy sprzężona z płcią letalna cecha recesywna jest tak samo podatna na wyeliminowanie przez dobór jak letalna cecha niesprzężona z płcią?

37. W populacji I częstość występowania genu recesywnego, sprzężonego z płcią wynosi 20%. W populacji II częstość występowania tego samego recesywnego genu sprzężonego z płcią wynosi 8%. Jaka jest częstość występowania wszystkich możliwych genotypów, gdy obie populacje ulegną zmieszaniu w wyniku krzyżowania równej liczby osobników, w ciągu kilku pokoleń?

38. W pewnej próbie z populacji ludzkiej stwierdzono obecność 23 osobników z grupą krwi AB, 441 z grupą 0, 371 z grupą B i 65 z grupą A.

a) Opracować metodę pozwalającą na wyliczenie frekwencji różnych alleli w oparciu o znane frekwencje różnych fenotypów.

b) Obliczyć frekwencję alleli I^A, I^B oraz i (odpowiednio p, q) w charakteryzowanej populacji.

c) Mając frekwencję alleli I^A = 0,36; I^B = 0,20; i = 0,44 obliczyć procent osobników o grupie krwi A, B, AB, 0.

39. Zbadano grupę krwi 160 losowo wybranym studentom. Okazało się, że grupę krwi A posiadają 64 osoby, grupę B - 38, AB - 20 i 0 - 38 osób.

a) Oblicz frekwencję genów (oznaczając częstości poszczególnych alleli literami p, q, r), genotypów i fenotypów.

b) Podaj, ilu osobników wśród studentów o identycznym fenotypie musi mieć ten sam genotyp.

40. Frekwencja alleli A i a w populacji wynosi odpowiednio: 0,4 i 0,6, podczas gdy alleli B i b odpowiednio 0,8 i 0,2. Te dwie pary genów dziedziczą się niezależnie. Wyliczyć frekwencję różnych genotypów pod względem tych dwóch par genów w populacji będącej w stanie równowagi genetycznej.

41. Załóżmy, że barwy: czarna lub czerwona u bydła zależą od pary genów B, b (B - wyznacza barwę czarną i jest genem dominującym). Rozmieszczenie barwnika zależy od pary genów J, j. Zwierzęta o genotypach JJ lub Jj są umaszczone jednolicie (czarne lub czerwone), natomiast zwierzęta o genotypach jj są łaciate. W stadzie złożonym z 400 sztuk krów pochodzących z kojarzeń losowych stwierdzono takie fenotypy:

czarne-łaciate - 51 sztuk,

czarne-jednolite - 153 sztuki,

czerwone-jednolite - 347 sztuk,

czerwone-łaciate - 49 sztuk.

Oblicz częstość podanych tu genów (p_B, q_b, r_J, s_j), genotypów i fenotypów oraz podaj, ile czarnych krów w tym stadzie jest nosicielami genu czerwonego umaszczenia, a ile krów umaszczonych jednolicie - genu łaciatości.

42. W rozmnażającej się losowo populacji 800 kur andaluzyjskich (72 czarne, 336 niebieskich i 392 białe) 288 ptaków miało grzebień groszkowy, reszta zaś prosty. Obie wymienione cechy - kształt grzebienia (groszkowy

dominuje nad prostym — para genów G, g) i barwa piór dziedziczą się niezależnie od siebie.

a) Oblicz frekwencję genów warunkujących barwę piór (p_A i q_a) i kształt grzebienia (r_G i s_g) w podanej populacji.

b) Ustal ile różnych fenotypów i z jaką częstotliwością wystąpiło w danym stadzie.

c) Ile było ptaków czarnych, białych i niebieskich heterozygotycznych pod względem kształtu grzebienia.

43. Umaszczenie myszy zależy od dwóch par genów A, a (gen A - wywołuje strefowe zabarwienie włosa zwane agouti, które dominuje nad jednolitym zabarwieniem wyznaczonym przez gen - a) i od pary genów B, b (gen B - daje włos czarny i dominuje nad genem - b, warunkującym włos brązowy, czekoladowy). Współdziałanie tych par alleli daje różne maści:

A - B - : dzikie;

A - bb : cynamonowe;

Aa B - : czarne, nie agouti;

Aa bb : czekoladowe, nie agouti.

W zrównoważonej genetycznie populacji złożonej z 20 000 myszy obliczono, że częstość genów warunkujących umaszczenie wynoszą: p_A = 0,9; q_a = 0,1; r_B = 0,4; s_b = 0,6.

a) Ile myszy o poszczególnych maściach należy oczekiwać w tej populacji?

b) Ile myszy będzie wiernie przekazywało swoje cechy na potomstwo (bez rozszczepień)?

44. Barwa oczu u Drosophila zależy od pary genów W, w umieszczonych w chromosomach płci. Oczy czerwone (gen -W) dominują nad białymi (gen -w). W zrównoważonej genetycznie populacji 2000 sztuk tych much stwierdzono, że częstość występowania genu w wynosi 0,4.

a) Oblicz, ile należy oczekiwać much o oczach białych;

b) Ile much jest nosicielami genu na białe oczy (osobniki o cesze dominującej) i jaka jest ich płeć?

45. Chłopiec kupił 4 pary królików: dwie czystorasowe (a więc homozygotyczne) czarne, jedną białą (także homozygotyczną - genotyp cc) i jedną parę czarnych mieszańców (jedno z ich rodziców miało futerko białe).

a) Czy ta mała „populacja" złożona z 8 królików jest w równowadze genetycznej?

b) Ustal oczekiwaną strukturę genetyczną w pokoleniu F₁ powstałym na drodze kojarzeń losowych zakupionych królików.

c) Załóżmy, że każda samica i każdy samiec pozostawili po sobie tę samą liczbę potomstwa, i że po pewnym czasie pokolenie F₁ liczyło 140 królików. Ilu królików o umaszczeniu czarnym i białym należy spodziewać się w tym pokoleniu?

46. W rozmnażającej się losowo populacji kur andaluzyjskich frekwencja genu warunkującego barwę czarną p_A równa się 0,3, zaś barwę białą q_a równa się 0,7. 1000 sztuk kur losowo wybranych z tej populacji skojarzono z kogutami wyłącznie niebieskimi (osobniki o genotypach Aa).

a) Jaki rozkład genów, genotypów i fenotypów może wystąpić w pokoleniu F₁ otrzymanym na drodze kojarzeń losowych wybranych kur i niebieskich kogutów.

b) Porównaj strukturę genetyczną dwóch populacji: F₁ i rodzicielskiej.

47. W rozmnażającej się losowo populacji kur andaluzyjskich częstość występowania genów wyznaczających barwę upierzenia (czarne - genotypy AA, niebieskie - Aa, białe - aa) są następujące: p_A = 0,6; q_a = 0,4. Po pewnym czasie zaprzestano kojarzeń losowych i podzielono losowo całą populację kur na dwa stada. W pierwszym z nich zastosowano system kojarzeń podobny z podobnym, a w drugim niepodobny z niepodobnym.

a) Ustal i porównaj oczekiwaną strukturę genetyczną w pokoleniu F₁ otrzymanym w każdym z opisanych stad kur przy przyjętych w nich systemach kojarzeń.

b) Czy w tych pokoleniach F₁ populacje będą w równowadze genetycznej? Odpowiedź uzasadnij.

Odpowiedzi do powyższych zadań:

1. a) p_A= 0,55, q_a=0,45; b) populacja nie jest w stanie równowagi, osiągnie ją, gdy będą częstości: AA = 0,3025, Aa = 0,495, aa = 0,2025.

2. Częstość osobników zdolnych i niezdolnych do zwijania języka wynoszą odpowiednio 0,64 i 0,36.

3. p_A = 0,7; q_a = 0,3.

4. a) Częstość genu C^R = 0,6; częstość genu c^w = 0,4; b) 0,36 C^RC^R : 0,48 C^RC^W: 0,16C^WC^W.

5. Częstość genu C^B = 0,89; częstość genu C^Y = 0,11.

6. P_B = 0,9; q_b = 0,l.

7. p_Rh+ = 0,613; q_Rh^_ = 0,387.

8. RR - 0,81; Rr - 0,18.

9. a) p_Rh+ = 0,6; q_Rh- = 0,4; b) RR (0,36) : Rr (0,48) : rr (0,16).

10. TT = 0,20; Tt = 0,50.

11. q_t = 0,51.

12. Tak (idealny wynik 4 : 392: 9604).

13. 0,125.

14. 0,645.

15. 13.

16. C^G = 0,1; C^D = 0,9.

17. 0,5; wszystkie osobniki będą miały genotyp Aa.

18. a) HH (0,36); Hh (0,48); hh (0,16); b) HH - 342; Hh - 456.

19. a) p_b+ = 0,85; q_b = 0,15; b) homozygot szarych 1445, heterozygot 510.

20. a) Nie; b) p_vg+ = 0,8; q_vg = 0,2; vg⁺vg⁺ (0,65); vg⁺vg (0,31); vgvg (0,04); 96% much skrzydlatych i 4% bezskrzydłych; c) populacje różnią się. Populacja w F₁ znajduje się w równowadze genetycznej.

21. a) p_b+= 0,6; q_b= 0,4; b) nie; c) częstości genów j.w. b⁺b⁺ (0,36) : b⁺b (0,48) : bb (0,16); szare 0,84, czarne 0,16.

22. a) p_C = 0,6; q_c = 0,4; CC (0,4) : Cc (0,4) : cc (0,2); b) nie.

23. 6.

24. f).

25. b) i d).

26. a) 0,04 = 4%; b) 0,01 = 1%.

27. a) BB (0,49) : Bb (0,42) : bb (0,09) - równowaga genetyczna; np. BB (0,49) : Bb (0,46) : bb (0,05) - brak równowagi; b) w podanym przykładzie, gdy zwiększy się liczba homozygot recesywnych.

28. a) p = 0,96; b) 99,84%.

29. 0,64%.

30. a) 30 000 mężczyzn, 900 kobiet; b) kobiety - 58 200.

31. a) 0,01; b) 0,0001.

32. a) q_w = 0,15; p_w+ = 0,85; b) 2,25.

33. U kobiet białych 0,64%, u Murzynek 0,16%.

34. 1%.

35. a) 18%; b) 19%.

36. Gen eliminuje się częściej, ponieważ w każdym pokoleniu będą eliminowane samce obarczone tym genem.

37. Samice TT (0,7396) : Tt (0,2408) : tt (0,0196); samce T/- (0,86) : t/- (0,14).

38. a) r_i = √0, p_IA = 1 - √B + 0 , q_IB = 1 - √A + 0, gdzie A, B, 0 są to odpowiednie frekwencje fenotypów z grupami A, B i 0; b) r = 0,70, częstość genu I^A = 0,05, częstość genu I^B = 0,25; c) A = 44,6%, B = 21,6%, AB = 14,4%, 0 = 19,4%.

39. a) p_IA = 0,3108, q_IB = 0,2016, r_i = 0,4873; frekwencja fenotypów: A - 0,4; B - 0,2375; AB - 0,1250; 0 - 2375; frekwencja genotypów: I^AI^A - 0,096; I^Ai - 0,303; I^BI^B - 0,041; I^Bi - 0,196; I^AI^B - 0,125; ii - 0,238; b) 58 osób.

40. (0,16 AA : 0,48 Aa : 0,36 aa) x (0,64 BB : 0,32 Bb : 0,04 bb) = 0,1024 AABB : 0,0512 AABb : 0,0064 AAbb : 0,3072 AaBB : 0,1536 AaBb : 0,0192 Aabb : 0,2304 aaBB : 0,1152 aaBb : 0,0144 aabb.

41. p_B = 0,3; q_b = 0,7; r_J = 0,5; s_j = 0,5; BB (0,09) : Bb (0,42) : bb (0,49); JJ (0,25) : Jj (0,5) : jj (0,25); 168 krów czarnych nosicielek czerwonego umaszczenia; 200 krów umaszczonych jednolicie, nosicielek genu łaciatości.

42. a) p_A = 0,3; q_a = 0,7; r_G = 0,2; s_g = 0,8; b) czarne, grzebień groszkowy 0,0324; czarne, grzebień prosty 0,0576; andaluzyjskie, grzebień groszkowy 0,1512; andaluzyjskie, grzebień prosty 0,2688; białe, grzebień groszkowy 0,1764; białe, grzebień prosty 0,3136; c) czarne 23, andaluzyjskie 108, białe 125.

43. a) A-B- 12672, A-bb 7128, aaB- 128, aabb 72; b) 8528 myszy (AABB - 2592, AAbb - 5832, aaBB - 32, aabb - 72).

44. a) Samic 160, samców 400; b) 480 samic.

45. a) Nie jest w równowadze; b) CC (0,39), Cc (0,47), cc (0,14); c) czarnych 120, białych 20.

46. a) p_A = 0,4 q_a= 0,6; AA (0,16) : Aa (0,48) : aa (0,36); b) nastąpiło zwiększenie liczby osobników białych.

47. a) Podobne AA (0,48) : Aa (0,30) : aa (0,22); niepodobne AA (0,28) : Aa (0,59) : aa (0,13); b) nie będą w stanie równowagi.

Opracowała Kinga Boruszewska

---