WOJSKOWA AKADEMIA TECHNICZNA

WYDZIAŁ MECHATRONIKI

INSTYTUT SYSTEMÓW MECHATRONICZNYCH

Teoria sterowania

Laboratorium 2

METODY OPISU UKŁADÓW LINIOWYCH, STACJONARNYCH.

BADANIE STEROWALNOŚCI I OBSERWOWALNOŚCI LINIOWEGO UKŁADU DYNAMICZNEGO

Złożone obiekty sterowania zazwyczaj mają kilka wejść i kilka wyjść, pomiędzy którymi mogą występować złożone sprzężenia skrośne. Aby dla takich obiektów przeprowadzić analizę układów sterowania, istotne staje się zredukowanie złożoności wyrażeń matematycznych i uporządkowanie ich celem wykonania koniecznych i żmudnych obliczeń. Z tego punktu widzenia analiza w przestrzeni stanów jest najdogodniejsza.

Podczas gdy konwencjonalna teoria sterowania opiera się na zależnościach wejściowo-wyjściowych lub transmitancji to nowoczesna teoria sterowania opiera się na opisie układu przy użyciu n równań różniczkowych pierwszego rzędu, które mogą być połączone w równania różniczkowe wektorowo-macierzowe. Użycie notacji wektorowo-macierzowej wydatnie upraszcza opis matematyczny układów modelowanych przy wykorzystaniu równań różniczkowych zwyczajnych stacjonarnych.

1. Część teoretyczna. Metody opisu układów liniowych, stacjonarnych

Wariant 1. Równania różniczkowe

Układy sterowania mogą być modelowane przez równania różniczkowe. Ogólnie, układ jest opisany równaniem n- tego rzędu

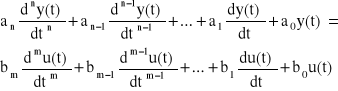
(1)

gdzie n > m. Większość układów fizycznych jest nieliniowa i musi być opisywana przez nieliniowe równania dynamiczne.

Wariant 2. Transmitancja operatorowa

Poprzez zdefiniowanie operatora s jako

(2)

oraz zapisaniu sygnału wejścia u(t) i wyjścia y(t) w postaci operatorowej, równanie (1) może zostać zapisane następująco

(3)

Widać stąd, że dla układu opisanego równaniem różniczkowym (1) w łatwy sposób może być wyznaczona transmitancja operatorowa

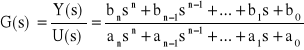
(4)

Wariant 3. Równania dynamiczne - przestrzeń stanu

Możliwe jest również przekształcenie opisu układu do postaci równań dynamicznych. Może to być zrealizowane zarówno na podstawie transmitancji jak i równania różniczkowego, bądź równania dynamiczne mogą zostać zdefiniowane na etapie modelowania układu sterowania.

Równanie różniczkowe n- tego rzędu (1) może być zdekomponowane na n równań różniczkowych pierwszego rzędu. Równania różniczkowe pierwszego rzędu są łatwiejsze do rozwiązania niż równania wyższego rzędu i jest to powodem, dla którego są one stosowane w analizowaniu układów sterowania.

Dla układu liniowego, stacjonarnego równania dynamiczne są zapisywane w postaci wektorowo-macierzowej jako:

Równania stanu

(5)

Równania wyjścia

(6)

gdzie: x(t) jest wektorem stanu, u(t) - wektorem wejścia, y(t) - wektorem wyjścia, A - macierzą stanu, B - macierzą wejścia, C - macierzą wyjścia oraz D - macierzą sprzężenia bezpośredniego, n -liczbą zmiennych stanu, p - liczbą wejść, q - liczbą wyjść.

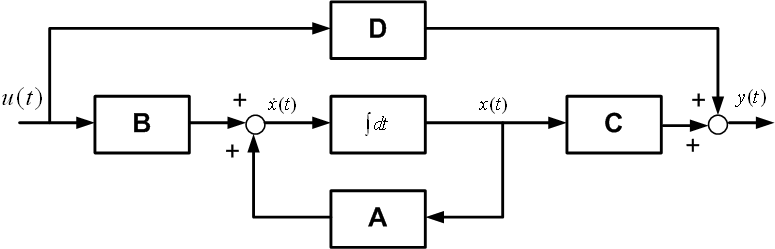
Zapis równań (5) i (6) w postaci schematu blokowego jest przedstawiony na rysunku 1.

Rys. 1. Schemat blokowy ciągłego liniowego układu sterowania w przestrzeni stanów

2. Część praktyczna. Modelowanie układu dynamicznego.

Dany jest układ składający się z trzech elementów: masy m, sprężyny k oraz tłumika c. Układ wymuszany jest siłą F(t). Położenie masy w każdej chwili czasu określone jest współrzędną x (jeden stopień swobody).

Rys. 2. Model układu dynamicznego o jednym stopniu swobody

Zakładamy, że układ jest liniowy. Wejściem układu jest siła F(t) a wielkością wyjściową przemieszczenie masy y(t). Układ taki jest układem z jednym wejściem i jednym wyjściem i można go opisać za pomocą transmitancji. Tutaj zostanie pokazana możliwość równoważnego opisu układu w przestrzeni stanu. Ze schematu otrzymujemy równanie układu:

(7)

gdzie:

m - masa [kg],

c - współczynnik tłumienia wiskotycznego [Ns/m],

k - współczynnik sztywności [N/m].

Układ przedstawiony na rysunku 2 w systemie MATLAB-SIMULINK można zamodelować na kilka sposobów.

Sposób 1.

Równanie (7) to równanie różniczkowe drugiego rzędu, co oznacza, że w skład układu wchodzą dwa integratory. Zdefiniujemy zmienne stanu x₁(t) i x₂(t) jako:

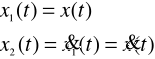
(8)

Podstawiając za
i
zastępujemy równanie różniczkowe drugiego rzędu, układem dwóch równań rzędu pierwszego w postaci:

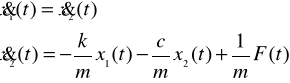
(9)

Równanie wyjść ma postać:

(10)

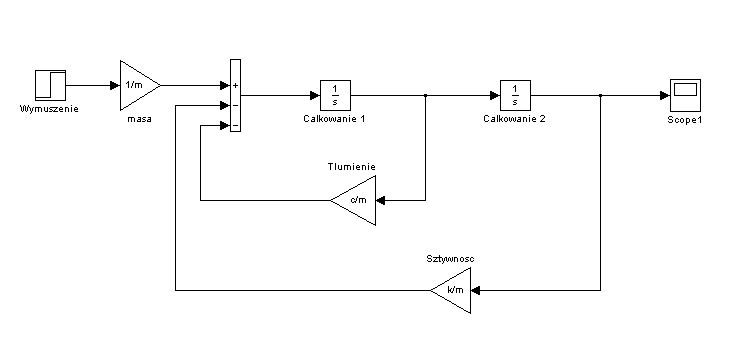
Równanie (9) można przedstawić w postaci schematu blokowego przedstawionego na rysunku 1.2.

Rys. 3. Schemat blokowy układu o jednym stopniu swobody zbudowany z bloków Integrator (całkujących)

Sposób 2

Dokonując przekształcenia Laplace'a równania (7) otrzymujemy:

11)

(12)

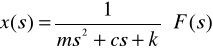
(13)

Równanie (13) można przedstawić w postaci schematu blokowego pokazanego na rysunku 4.

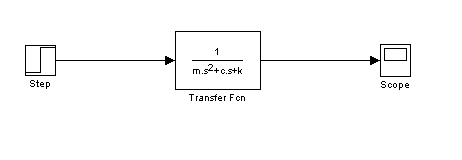
Rys. 4. Schemat blokowy układu o jednym stopniu swobody zbudowany z bloku Transfer Fcn (funkcja przejścia)

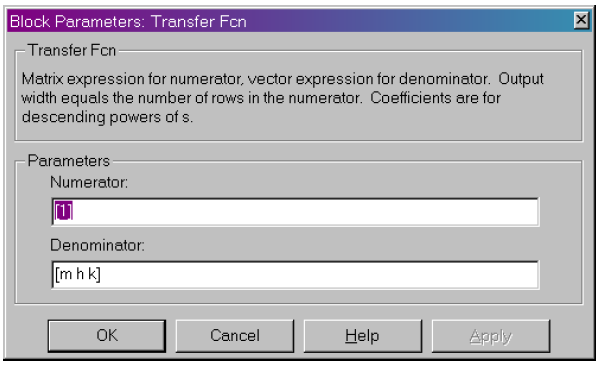
Parametry bloku Transfer Fcn powinny być ustawione jak na rysunku 5.

Rys. 5. Parametry bloku Transfer Fcn (funkcja przejścia) dla układu o jednym stopniu swobody

Wariant 3

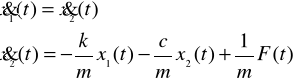
(14)

W postaci wektorowo- macierzowej równania (14) mogą być zapisane w następującej postaci:

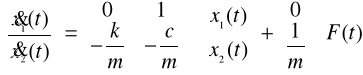
(15)

Uzupełniając równanie (10) równaniem w postaci:

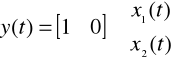
(16)

otrzymujemy układ równań zwany uogólnionym równaniem stanu. Równanie (15) jest równaniem stanu a równanie (16) równaniem wyjść dla układu.

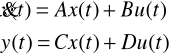
(17)

gdzie:

,
,
,
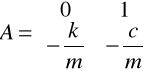
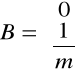
(18)

gdzie:

x(t) - wektor stanu, u(t) - wektor wymuszeń, y(t) - współrzędna odpowiedzi, A - macierz stanu, B - macierz wymuszeń, C - macierz odpowiedzi, D - macierz transmisyjna.

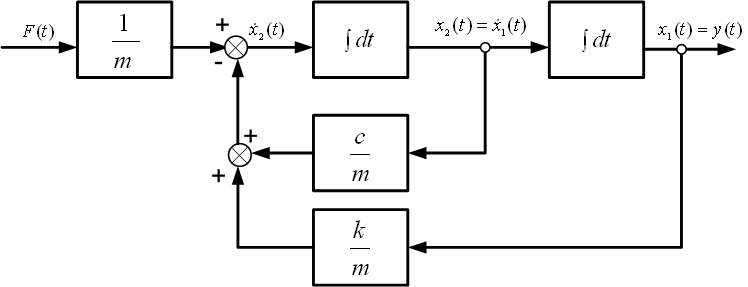
Rysunek 6 jest schematem blokowym układu. Należy zauważyć, że sygnały wyjściowe po scałkowaniu są zmiennymi stanu.

Rys. 6. Schemat blokowy układu mechanicznego

Wykorzystując równanie stanu (17) układ o jednym stopniu swobody można przedstawić w postaci schematu blokowego przedstawionego na rysunku 7.

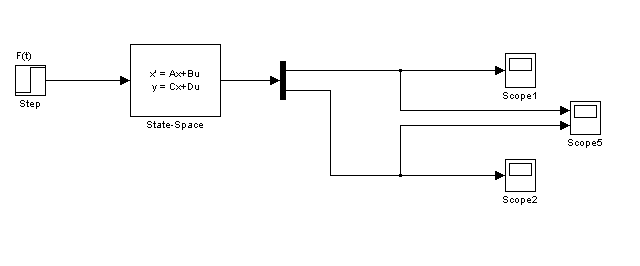
Rys. 7. Schemat blokowy układu o jednym stopniu swobody zbudowany z bloku State-Space (przestrzeni stanu)

Parametry bloku State-Space powinny być ustawione jak na rysunku 8.

Rys. 8. Parametry bloku State-Space dla układu o jednym stopniu swobody

3. Przebieg ćwiczenia

A1. Zbudować w SIMULINKU schemat układu przedstawionego na rysunku 2 wykorzystując bloki INEGRATOR zgodnie z rysunkiem 3. Zarchiwizować uzyskane rozwiązania na dysku i wykonać stosowne wykresy.

A2. Zbudować w SIMULINKU schemat układu przedstawionego na rysunku 2 wykorzystując blok TRANSFER FCN (funkcja przejścia) zgodnie z rysunkiem 4. Zarchiwizować uzyskane rozwiązania na dysku i wykonać stosowne wykresy.

A3. Zbudować w SIMULINKU schemat układu przedstawionego na rysunku 2 wykorzystując blok STATE-SPACE zgodnie z rysunkiem 7. Zarchiwizować uzyskane rozwiązania na dysku i wykonać stosowne wykresy.

A4. Wykorzystując jeden z realizowanych modeli wyznaczyć następujące parametry:

• współczynnik proporcjonalności (wzmocnienia),

• stałą czasu,

• współczynnik tłumienia.

A5. Zbadać model matematyczny rozpatrywanego układu dynamicznego dla następujących wartości współczynnika tłumienia: ζ1 = 0, ζ2 = 0.2, ζ3 = 0.7, ζ4 = 1, ζ5 = 2. Zarchiwizować uzyskane rozwiązania na dysku i wykonać stosowne wykresy. Przedstawić stosowne wnioski końcowe.

A6. Zbadać sterowalność i obserwowalność rozpatrywanego układu dynamicznego.

4. Sprawozdanie z przebiegu ćwiczenia

Na podstawie przeprowadzonych symulacji należy przygotować sprawozdanie, które powinno zawierać zrealizowane na zajęciach modele matematyczne i ich schematy blokowe, otrzymane wyniki symulacji, oraz wnioski końcowe.

Literatura

[1] Brzózka J., Ćwiczenia z Automatyki w MATLABIE i SIMULINKU, Wydawnictwo Mikon,Warszawa 1997.

[2] Tomera M., Wprowadzenie do MATLABA, 2004.

[3] Zalewski A., Cegieła R., MATLAB: obliczenia numeryczne i ich zastosowania, Wydawnictwo Nakom, Poznań 1996.

---