1-04-2012
IEF-ZI
Laboratorium z fizyki
Ćw. nr: 1A
Temat:
Wyznaczanie przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego
Damian Kulpa
LP 3
Cel ćwiczenia.
Celem ćwiczenia jest wyznaczanie przyśpieszenia ziemskiego za pomocą wahadła rewersyjnego.
Zagadnienia teoretyczne.
Newtonowskie prawo powszechnego ciążenia stwierdza, że wszelkie ciała oddziaływują ze sobą wzajemnie siłą przyciągania skierowaną wzdłuż prostej łączącej środki mas obu ciał i mającą wartość:
F= γ ⋅ ![]()
gdzie:
M1 , M2 - masy oddziaływujących ciał
R - odległość między środkami mas
γ - stała grawitacyjna
γ = 6,67⋅10![]()
Ciężar to siła, która nadaje ciałom przyśpieszenie ziemskie:
Q = m* g
gdzie:
Q - ciężar ciała
m - masa ciała
g - wektor przyśpieszenia ziemskiego, g ≈ 9,81
Ruch drgający harmoniczny prosty to ruch, w którym następuje okresowa zmienność określonej wielkości fizycznej np. przemieszczenia x.
F = - k ⋅ x
gdzie:
k - współczynnik proporcjonalności
m![]()
= - k ⋅ x
![]()
+ ⋅ x = 0
x = A cos (w t + γ ) - część koła
= ![]()
x = A cos [ ( t + ) + δ ] = A cos ( t + 2 + δ ) = A cos ( t + δ )
T = = 2![]()
T - okres drgań
Wahadło matematyczne jest to wyidealizowane ciało o punktowej masie zawieszone na cienkiej, nierozciągliwej i nieważkiej nici.
gdzie:
l - długość nici
N - naprężenie
γ - kąt odchylenia nici od pionu
Wahadło fizyczne jest to dowolne ciało sztywne mogące obracać się w poziomej osi nie przechodzącej przez środek jego masy.
gdzie:
C - środek ciężkości
a - odległość punktu A od środka masy
b - odległość punktu B od środka masy
Jeśli oś obrotu przechodzi przez punkt A to okres drgań wahadła fizycznego względem tego punkt ma wzór:
TA = 2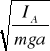
gdzie:
IA - moment bezwładności
IA = I0 + ma
gdzie:
I - moment bezwładności względem osi przechodzącej przez środek masy
TA = 2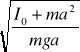
TB = 2 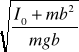
TA = TB
2 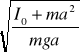
= 2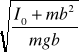
I0 (a - b) = mab (a - b) gdy a b I 0 = mab
TA = TB = 2 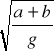
l zr = a + b
mamy zatem : TA = TB = 2 ![]()
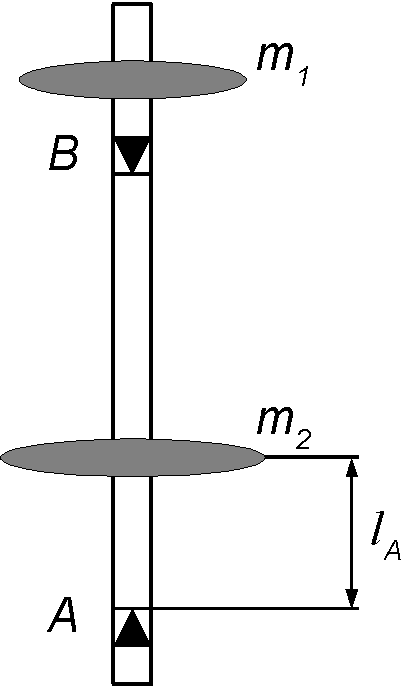
Wahadło rewersyjne składa się z metalowego pręta zaopatrzonego w dwie pary ostrzy, które znajdują się w stałej odległości. Służą one do zawieszania wahadła na odpowiedniej podstawce. Obok ostrzy, na pręcie znajdują się dwie masy: m1 - umocowana na stałe i m2 - ruchoma.
Masę m2 można przesuwać wzdłuż pręta pomiędzy punktami A i B zmieniając w ten sposób położenie środka masy wahadła. Przy pewnym położeniu masy m2 na pręcie okres wahadła rewersyjnego T przy zawieszeniu zarówno na ostrzu O1 jak i O2 będzie identyczny. Wyznaczając ten okres drgań i mierząc odległość między ostrzami równą długości zredukowanej wahadła rewersyjnego lr możemy obliczyć przyspieszenie ziemskie ze wzoru:
Metodologia wykonania pomiarów.
Zawiesić wahadło rewersyjne na ostrzu B i ustawić masę m2 w pobliżu ostrza A.
Wprawić wahadło w ruch (wychylenie
dla każdego wzbudzenia takie samo) i zmierzyć za pomocą sekundomierza czas t dziesięciu wahnięć i wyliczyć wartość okresu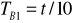
.Następnie odwrócić wahadło i zawiesić je na ostrzu A i podobnie jak punkcie 2 wyznaczyć wartość okresu
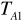
.Przesunąć masę m2 o 5 cm w stronę B i ponownie wyznaczyć okres drgań
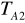
dla zawieszenia A.Wahadło odwrócić, zawiesić na ostrzu B i zmierzyć TB2.
Powtórzyć pomiary wg. punktów 4,5 i znaleźć dwa szeregi wartości okresów TA1, TA2, ...TAn i TB1, TB2, ... TBn dla wszystkich możliwych położeń masy m2 pomiędzy zawieszeniami A i B w odstępach co 5 cm. Wyniki zapisać w tabeli.
Tabela pomiarów.
L(an) |
t(an) |
t(bn) |
T An |
T Bn |
L® |
T |
g+-delta(g) |
10 |
23,53 |
23,53 |
2,35 |
2,35 |
1,3 |
|
|
15 |
23,38 |
22,78 |
2,34 |
2,28 |
1,3 |
|
|
20 |
22,78 |
22,69 |
2,28 |
2,27 |
1,3 |
|
|
25 |
22,59 |
22,34 |
2,26 |
2,23 |
1,3 |
|
|
30 |
22,07 |
22,31 |
2,21 |
2,23 |
1,3 |
|
|
35 |
21,66 |
22,19 |
2,17 |
2,22 |
1,3 |
|
|
40 |
21,44 |
21,95 |
2,14 |
2,20 |
1,3 |
|
|
45 |
21,13 |
21,85 |
2,11 |
2,19 |
1,3 |
|
|
50 |
20,84 |
21,71 |
2,08 |
2,17 |
1,3 |
|
|
55 |
20,53 |
21,75 |
2,05 |
2,18 |
1,3 |
|
|
60 |
20,25 |
21,7 |
2,03 |
2,17 |
1,3 |
|
|
65 |
19,93 |
21,8 |
1,99 |
2,18 |
1,3 |
|
|
70 |
19,87 |
21,72 |
1,99 |
2,17 |
1,3 |
|
|
75 |
19,66 |
21,66 |
1,97 |
2,17 |
1,3 |
|
|
80 |
19,5 |
21,83 |
1,95 |
2,18 |
1,3 |
|
|
85 |
19,47 |
21,78 |
1,95 |
2,18 |
1,3 |
|
|
90 |
19,44 |
22,19 |
1,94 |
2,22 |
1,3 |
|
|
95 |
19,53 |
22,22 |
1,95 |
2,22 |
1,3 |
|
|
100 |
20,12 |
22,31 |
2,01 |
2,23 |
1,3 |
|
|
105 |
21,25 |
22,72 |
2,13 |
2,27 |
1,3 |
|
|
110 |
22,03 |
22,81 |
2,20 |
2,28 |
1,3 |
|
|
115 |
23,53 |
22,97 |
2,35 |
2,30 |
1,3 |
|
|
120 |
26,34 |
23,16 |
2,63 |
2,32 |
1,3 |
|
|
Obliczenia:
Δl = 1 mm = 0,001m
Δt = 0,2s
Obliczanie niepewności u(l) i u(t) metodą typu B oraz niepewność ΔT z prawa przenoszenia niepewności
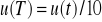
.
![]()
![]()
![]()
3) Obliczanie średniej arytmetycznej okresu drgań T
Punkty T1 i T2 odpowiadają punktom przecięcia się krzywych Ta i Tb
![]()
4) Obliczanie przyśpieszenia ziemskiego.
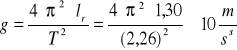
5) Obliczanie niepewności przyśpieszenia ziemskiego (g) z prawa przenoszenia niepewności.
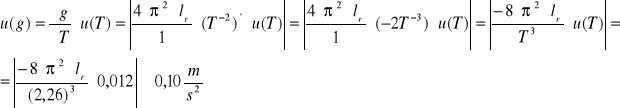
6) Przyśpieszenie ziemskie według tablic fizycznych wynosi w przybliżeniu g=9,81![]()
Podczas doświadczeń z wahadłem rewersyjnym udało nam się osiągnąć przyśpieszenie równe g=10 ![]()
,
Wykres
Wnioski
Wyliczona ze wzoru wartość przyspieszenia ziemskiego wynosi 10![]()
i odbiega od wartości tablicowej 9,81![]()
. Niedokładność wynika z takich czynników jak: czas reakcji człowieka przy pomiarze stoperem czy niedokładnie zmierzona odległość masy od ostrza.
9
Wyszukiwarka