Opracowanie: Jakub Wyrostek

WYKŁAD 1

Uzupełnienie rachunku różniczkowego funkcji jednej zmiennej

LEMAT 1.1 (Fermata, o zerowaniu się pochodnej)

Z:

T:

Dowód jest następujący:

Niech dla przykładu:

Wiemy wówczas, że:

Stąd dla
:
.

Natomiast dla
:
,

a wobec faktu, że granica przy
istnieje, wnioskujemy, że
.

(Dowód dla min jest analogiczny.)

TWIERDZENIE 1.1 (Rolle'a)

Jeśli funkcja
jest określona i ciągła w przedziale domkniętym
, istnieje pochodna skończona przynajmniej w przedziale otwartym
i na końcach przedziału funkcja przyjmuje równe wartości, wówczas między
i
można znaleźć taki punkt
, że
.

Z:

T:

Dowód obejmuje dwa przypadki:

1º Funkcja jest stała. Wówczas:

2º Funkcja jest różnowartościowa (
).

Dla dowodu przyjmijmy, że:

,

a ponieważ funkcja jest ciągła i przyjmuje takie same wartości na krańcach przedziałów, wobec tego
. Stąd na podstawie Lematu 1.1 wnioskujemy, iż

.

TWIERDZENIE 1.2 (Cauchy'ego)

Jeśli funkcje
i
są określone i ciągłe w przedziale domkniętym
, istnieją pochodne skończone przynajmniej w przedziale otwartym
i
w przedziale
, wówczas między
i
można znaleźć taki punkt 
, że:

Z:

T:

Dowód:

Wiedząc, że
wnioskujemy, iż
. Możemy zatem wprowadzić nową funkcję:

.

Możemy wyliczyć
, oraz
. A ponieważ z własności kombinacji funkcji ciągłych wnioskujemy, że
, przeto możemy zastosować twierdzenie 1.1:

.

Wyliczając pochodną
, przyrównując ją do zera i przekształcając, otrzymujemy tezę.

TWIERDZENIE 1.3 (Lagrange'a, szczególny przypadek twierdzenia Cauchy'ego)

Z:

T:

Dowód:

Jest to szczególny przypadek twierdzenia Cauchy'ego, dla
.

Inne postacie twierdzenia Lagrange'a.

Jeśli przyjmiemy
i
, wówczas możemy zauważyć, że wyrażenie

da się przekształcić (przez wymnożenie licznika i mianownika ułamka przez (
)) w:

gdzie
i
. Czyli twierdzenie nie zależy od “kolejności”
i
.

Twierdzenie możemy więc zapisać w następujący sposób:

Z:
, gdzie
oraz
.

T:

Wyliczanie wartości przybliżonej funkcji.

Jeśli przyjmiemy
, wtedy:
, gdzie

wówczas teza twierdzenia Lagrange'a przyjmie postać:

,

skąd wyliczyć możemy
.

Możemy więc wysnuć wniosek 1.1

WNIOSEK 1.1

Z:
, gdzie
oraz
.

T:

PRZYKŁAD 1.1

Obliczymy
.

Przyjmujemy
,
,
i obliczamy:

A więc:
.

TWIERDZENIE 1.4 (Wzór Taylora)

Z:

T:

,

gdzie
nazywamy resztą Lagrange'a.

Dowód:

Przyjmiemy
. Wprowadzimy nowe funkcje:

, gdzie
,

.

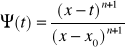
Na podstawie swoich własności obie te funkcje spełniają założenia twierdzenia Cauchy'ego. Obliczmy ich pochodne:

,

.

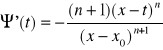
Zauważmy teraz, że:

Wykorzystamy teraz twierdzenie Cauchy'ego:

,

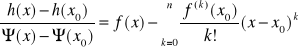
a z drugiej strony

.

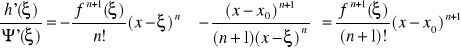
A więc:

,

co jest przekszatałceniem tezy twierdzenia.

Inne postacie twierdzenia Taylora. Rozwinięcia funkcji.

Powyższe twierdzenie możemy zapisać również w następujący sposób:

Z:

T:

,

Wzór ten pozwala obliczać przybliżone wartości funkcji. Ilustruje to następujący:

PRZYKŁAD 1.1 cd

Obliczymy ponownie
z dokładnością do
. Ustalmy liczbę kroków
. Rozpisujemy wzór Taylora:

Przyjmujemy
,
,
i obliczamy pochodne:

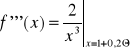
A więc:
.

Teraz szacujemy resztę, by sprawdzić, czy otrzymana wartość logarytmu mieści się w zadanej dokładności. Przyjmujemy
, gdyż funkcja ma wówczas największą wartość.

.

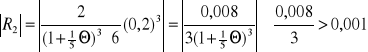
Zadana reszta jest więc większa od żądanej dokładności. Musimy zatem wziąć większe
.

Weźmy
. Wówczas:

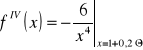
Zatem
z żądaną

dokładnością mniejszą niż 0,001.

Wzór Taylora w otoczeniu zera.

Przyjmiemy
(
). Otrzymujemy:

TWIERDZENIE 1.5 (MacLaurina)

Z:

T:

, gdzie
.

NIESKOŃCZENIE MAŁE

DEFINICJA 1.1

Jeżeli
oraz
, wówczas
nazywamy nieskończenie małą w
.

PRZYKŁAD 1.2

Funkcje

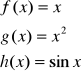
są nieskończenie małe w otoczeniu w otoczeniu
.

DEFINICJA 1.2

Niech
- nieskończenie małe w
,

1.
i mówimy, że
jest nieskończenie małą rzędu wyższego niż
.

2.
i
są nieskończenie małe w otoczeniu
tego samego rzędu

3.
i
są nieskończenie małe w otoczeniu
równoważne

.

UWAGA 1.1

Reszta we wzorze MacLaurina jest w otoczeniu zera nieskończenie małą rzędu wyższego niż
, co zapisujemy:

.

Uzasadnienie:

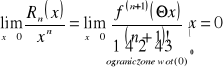
WNIOSEK 1.2

Tezę twierdzenia MacLaurina można zapisać w następujący sposób:

, gdzie
jest tzw. resztą Peano.

PRZYKŁAD 1.3

1º

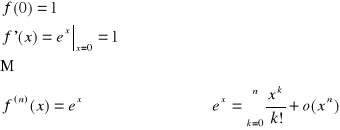
2º

Analogicznie postępując jak wyżej możemy wyprowadzić wzór na cos x.

.

---