1. FOTOGRAMETRIA - dział nauki i praktyki zajmujący się określaniem położenia ( wyznaczenie współrzędnych x, y, z), wymiarów i kształtu obiektów przestrzennych na podst. ich obrazów fotograficznych. Obiektem pomiarów fotogram. jest przede wszystkim powierzchnia Ziemi
Fotogrametria dzieli się ze względu na:
# ilość wykorzystywanych zdjęć:
*dwuobrazowa - 3D (x, y, z) *jednoobrazowa - 2D (x, y) opracowanie pojedynczego zdjęcia
# miejsce wykonania zdjęć:
*naziemna TERRO - zdj. z ziemi *lotnicza AERO *satelitarna
# met. opracowania:
*analogowa -posługuje się met. ciągłego przetwarzania obrazu na drodze instrumentalnej *analityczna - met. oprawco. zdjęć na drodze analit. Efekt -otrzymanie wys. p-któw
2. KAMERY LOTNICZE
Kamera fotogram. (pomiarowa kamera lotnicza) - urządzenie do pozyskiwania zdjęć lotnicz. Są to bardzo dokładne i skomplikowane układy mechaniczne, elektryczne, optyczne i elektroniczne.
Kamera składa się z:
Obiektywu (wolnego od dystorsji) wyposażonego w zmienną lub stałą przysłonę i urządzenie do regulacji czasu naświetlania filmu
Korpusu kamery, wyposażonego w szlifowaną ramkę tłową ze znaczkami tłowymi, a także uchwyt na kasety lub ładownik z materiałem negatywowym. Ramka tłowa zazwyczaj znajduje się w płaszcz. ognisk. obiektywu i jest prostopadła do osi obiektywu.
Urządzeń umożliwiających realizację określonej orientacji zewnętrznej (GPS, celownik, komputer)
Kaset lub ładowników
Zawieszenia lub spodarki ze statywem
Dodatkowego wyposażenia (np. filtr, statoskop, numerator zdjęć)
Wymagania konstrukcyjne kamer pomiarowych:
-obiektyw wolny od zniekształceń geometrycznych obrazu (szczególnie dystorsji)
-obiektyw powinien mieć dużą rozdzielczość
-konstrukcja podzespołów powinna gwarantować uzyskanie ostrego obrazu w ruchu
-powinna naświetlać znaczki tłowe
-ramka tłowa powinna być prostopadła do osi kamery
-powinna posiadać urządzenie do orientowania osi optycznej
Podział kamer lotniczych :
Kamery do wykonywania zdjęć pojedynczych - kadrowe (migawkowych obejmujących zasięgiem ramki tłowej wycinek fotografowanego obszaru)
Kamery szczelinowe (bez migawki), dostarczające ciągłego obrazu pasa terenu na przesuwającym się odpowiednio do prędkości lotu filmie.
Kamery panoramiczne.
Kamery kadrowe można sklasyfikować wg następujących kryteriów: orientacji wiązki, formatu, zasięgu pola widzenia, rodzaju emulsji i ilości obiektywów.
orientacja wiązki
-Kamery do wykonywania zdjęć prawie pionowych (w szeregach)
-Kamery do zdjęć perspektywicznych (o widocznej linii horyzontu)
-Kamery sprzężone - 2 kamery na wspólnym podwieszeniu o ustalonym kącie zbieżności osi kamer
Zasięg pola widzenia
-wąskokątne 10°-20° ck= 610,950mm
-normalnokątne 50°-75° ck= 210,300mm
-szerokokątne 85°-95° ck= 152mm
-ponad szerokokątne 110°-130° ck= 88mm
Odległość obrazu
Rodzaj emulsji:
- kamery z emulsją panchromatyczną (czarno-białą i barwną )
-kamery z emulsją podczerwoną (czarno-białą i barwną)
Ilość obiektywów
-jednoobiektywowe
-wieloobiektywowe
Wymiary zdjęcia:
-małoformatowe <18x18mmm,
-normalnego formatu 18x18, 23x23
-wielkoformatowe >23x23
Stopień automatyzacji (ręczne, półauto., auto)
Rodzaj podłoża materiału fotograficznego
Zakres promieniowania
Producenci: Wild, Carl Zeiss Jena, Opton
Cykl pracy. Na cykl ten składają się takie operacje, jak: odciągnięcie płyty dociskającej film od ramki tłowej, wyrównanie ciśnień, przewiniecie filmu, przyssanie filmu do płyty, dociśnięcie filmu do ramki tłowej, naciągnięcie i wyzwolenie migawki.
3. ZDJĘCIA ANALOGOWE
W zależności od położenia osi optycznej kamery lotniczej w momencie ekspozycji w stosunku do linii pionu przechodzącej przez przedni punkt główny obiektywu zdjęci lotnicze dzielimy na: Zdjęcia lotnicze dzielimy na:
Pionowe (v=0) i prawie pionowe v<3°(najczęściej opracowywane) do opracowania map topograficz. i inżynieryjno-gospodarczych
Nachylone v>3° -obejmują duży obszar rzadko stosowane do celów kartograficznych (v<45°)
Perspektywiczne (o dużym nachyleniu z odfotografowaną linią horyzontu) - do celów przeglądowych i rozpoznawczych
Zbieżne (o niedużym nachyleniu, osie kamer zbieżne - każde zdjęcie pokrywa tę samą część terenu)
Wg skali zdjęć:
Małoskalowe 25 000 < Mz < 100 000
Średnioskalowe 5 000 < Mz < 25 000
Wielkoskalowe 500 < Mz < 5 000
Zdjęcia wykonywane są szeregowo. Pokrycie wzajemne dwóch sąsiednich zdjęć w szeregu wynosi około 60% ich powierzchni.
W przypadku konieczności pokrycia zdjęciami lotniczymi większego obszaru, wykonywane są loty szeregowe z odpowiednimi odstępami pomiędzy osiami sąsiednich szeregów. Odstępy pomiędzy osiami szeregów zdjęć są tak dobrane, aby pokrycie poprzeczne Py wynosiło około 20% ich powierzchni. Podane wartości Px = 60% i Py = 30% są wartościami standardowymi. W określonych przypadkach mogą one być zmienione.
4. OBRAZ CYFROWY - jest to uporządkowany zbiór pikseli w postaci macierzy. Cechą pikseli jest poziom szarości w przedziale 0 - 255 dla obrazu czarno-białego (0-czarny, 255-biały). Człowiek rozróżnia 32-40 poziomów szarości. Podst. modelem kolorowego obrazu jest model RGB. Każdy piksel obrazu modelu RGB jest wypadkową zniesienia tych trzech barw. Natężenie tych barw mierzy się podobnie jak w przypadku obrazu czarno-białego - poziomami czerwoności, zieloności, niebieskości.
Wielkość piksela wiąże się z rozdzielczością skanowania
-zdolność rozdzielcza obiektywu - jest to cecha obiektywu związana z możliwością rozróżnienia bardzo małych obiektów na zdjęciu. Im mniejsze obiekty widzimy, tym większa rozdzielczość. Najłatwiej określić przez obserwacje linii biało - czarnej. Zdolność różni się na krawędziach i w centrum. Jakość obrazu cyfr. zależy od ilości pikseli tworzących ten obraz, im piksel jest większy tym rozdzielczość mniejsza.
-rozdzielczość emulsji fotograficznej - zależy od jej jakości i wynosi kilkadziesiąt linii podwójnych na milimetr
-zdolność rozdzielcza zdjęcia - rozdzielczość skanowania - dla takiego zdjęcia nie warto skanować z mniejszą rozdzielczością niż 20 mikrometrów. R = XxY R-rozdzielcz. X -ilość pikseli na osi poziom. Y -ilość pikseli na osi pionowej. Geometryczna rozdzielczość układu negatyw+obiektyw = 3880 dpi, przy czym piksel ma wielkość 7mikrometrów.
Rozdzielczość podajemy w DPI - liczba punktów na cal lub w PPI- piksel na cal.
Metody pozyskiwania:
Zdjęcie lotnicze w postaci cyfrowej powstaje dwoma sposobami:
I metoda - skanowanie - badany teren jest fotografowany zwykłą kamera lotnicza (rozdz. 3880dpi)
-zdjęcie lotnicze jest skanowane skanerem o rozdz. 1800dpi
-obraz cyfrowy dla opracowań fotogram. posiada rozdz. 1300dpi i zapisywany jest jako plik .bmp .tiff .gif
II metoda - zdjęcia terenu wykonywane są kamerą cyfrową o rozdzielcz. 3880dpi. Powstaje obraz cyfrowy o tejże rozdzielczości (bez straty informacji)
Typy skanerów i zasada digitalizacji obrazu.
Typy skanerów
mapowe - bębenkowe lub z linijką CCD
skanery do zdjęć lotniczych
Ze względu na okres rejestrowanego promieniowania
termalne (lub działające w podczerwieni) skanery liniowe (długa podczerwień)
wielospektralne (widzialna i termalna część widma)
Ze względu na sposoby działania wyróżniamy skanery
optyczno-mechaniczne - dokonują rejestracji terenu linią po linii - każdy piksel jest kolejno rejestrowany
elektrooptyczny - równoczesna rejestracja wszystkich pikseli należących do jednej linii
Skanery
kanałowe - posiada jeden detektor
wielokanałowe - posiada 2 lub więcej detektorów
elektroopty. powierzchn. CCD - zamiast linijki detektorów jest dwuwymiarowa matryca CCD zaw. N linijek czyli N*N detektorów
Dygitalizować - uzyskiwać z analogowej reprezentacji wielkości fizycznej zbliżone wielkości w postaci cyfrowej
Cechy obrazu cyfrowego
Geometryczne - rozdzielczość powierzchniowa-wymiar piksela w terenie.
określają geometrię obrazu
wymiar obrazu
liczbę pikseli na cal
wymiar pxl
układ wsp. pxl w lewym górnym narożniku
Radiomatyczne - rozdzielczość radiomatyczna - opisuję zasięg oraz dająca się wyróżnić liczbę określającą dyskretne wartości jasności
6 bit, 8 bitowy, 24 bit, 32 bi-czyli ilość bitów potrzebnych do zapisania obrazu cyfrowego
jasność obrazu cyfrowego
kontrastowość obrazu cyfrowego
Spektralne - podaje w jakim zakresie spektrum promieniowania elektromagnetycznego zarejestrowany jest obraz
5. PROTOKÓŁ KALIBRACJI KAMERY
Kalibracja kamer ma na celu dostarczenie charakterystyki metrycznej kamer fotogrametr. Taka charakteryst. jest niezbędna do przeprowadzenia prac fotogr. obejmuje następujące parametry:
*Odległość obrazowa kamery (stała kamery- ck lub f)
*Położenie punktu gł. kamery w stosunku do znaczków tłow. (xo,yo)
*Radialna i tangencjalna dystorsja obiektywu
*Odl. między znaczkami tłowymi
* Odchylenia ramki tłowej od płaszczyzny
Powyższe dane pozwalają na przeprowadzenie precyzyjnej geometrycznej rekonstrukcji wiązki promieni, która została zarejestrowana w kamerze podczas ekspozycji.. Metody kalibracji można podzielić na polowe i laboratoryjne. M. polwe wymagają budowy pola testowego lub wykorzystania wybranych gwiazd jako punktów o znanych współ. Do metod tych zalicza się metody statyczne i dynamiczne. Te ostatnie umożliwiają na przeprowadzanie kalibracji w czasie lotu. Najczęściej stosuje się jednak metody laboratoryjne, oparte na wykorzystaniu kalibratorów wielokolimatorowych lub goniometrów, czyli kalibrację przeprowadza się metodą fotograficzną lub wizualną.
6. GEOMETR. I RADIOMETRYCZNE ZNIEKSZTAŁC. OBRAZU
Zniekształcenia liniowe.
Wpływ nachylenia zdjęcia P-kt terenowy odwzoruje się na nachylonym zdjęciu lotniczym przesuniętym radialnie w kierunku punktu izocentrycznego, w porównaniu z jego odpowiednikiem na zdjęciu ściśle pionowym.
Wpływ deniwelacji Różnice terenowe powodują zniekształcenia perspektywistyczne punktów. Wpływ rozpatrzono na zdjęciach pionowych, gdyż wartość jest tego samego rzędu. Kierunek przesunięcia jest zgodny z kierunkiem do punktu nadirowego.
Zniekształcenia kątów o wierzchołkach w punktach głównych
Zniekształcenie spowodowane nachyleniem zdjęcia. Gdy zdjęcie jest nachylone o wartość kąta , to podczas pomiaru kierunków z punktu głównego, powstają błędy.
Zniekształcenie kierunku spowodowane deniwelacją terenu.
Przesunięcie radialne kierunków spowodowane deniwelacją terenu powoduje zniekształcenie kątowe kierunku mierzonego z punktu głównego.
Czynniki zniekształcające geometrię zdjęcia:
dystorsja obiektywu
deformacja podłoża emulsji fotograficznej
wpływ niepłaskości emulsji fotograficznej
wpływ refrakcji atmosferycznej
Dystorsja obiektywu lub dystorsja radialna - jest cechą stałą dla danego obiektywu. Jest to zniekształcenie obrazu rotacyjno-symetryczne, które jest cechą konstrukcyjną obiektywu. Zniekształcenie to powoduje radialne przemieszczenie obrazów punktów w kierunku do lub od punktu głównego zdjęcia i jest wynikiem różnego powiększania obrazów leżących w różnych odległościach kątowych od osi obiektywu. Dystorsję opisuje się przez podanie wektora określonej długości i kierunku. Oś obiektywu zazwyczaj nie jest linią prostą (oscyluje wokół domniemanej osi). Jeżeli w czasie montażu obiektywu, jego elementy optyczne nie zostały precyzyjnie scentrowane lub uzyskały niewielkie pochylenie, to będą działały w przybliżeniu jak mały pryzmat powodując decentrację dystorsji. Taką dystorsję określa się dwiema składowymi: radialną i tangencjalną
- charakter i wielkość dystorsji obiektywu zależą od konstrukcji obiektywu i umiejscowienia w nim diafragmy
- powstaje na skutek nierówności kątów wejścia i wyjścia promieni z obiektywu,
- na jej wartość wpływa dokładność montażu układu optycznego,
- charakterystyka podawana jest w postaci krzywej dystorsji,
- można ją wyeliminować jedną z czterech metod:
1. zasada Porro - Koppego,
2. stosowanie płyt kompensacyjnych
3. zmiana odległości obrazowej
4. metoda analityczna
- powoduje przesunięcie obrazu punktu na płaszczyźnie tłowej; przesunięcie to można rozłożyć na dwie składowe:
I rzut przesunięcia dystorsyjnego na promień radialny - dystorsja radialna
- II dystorsja tangencjalna.
Ta druga jest mała w porównaniu do pierwszej.
Wielkość przesunięcia radialnego zależy od kąta osiowego i długości promienia radialnego
Δr = r - ck * tg α
Dystorsja jest znana już przy projektowaniu obiektywu i najczęściej jest pomijana, gdyż jest ona bardzo mała.
Deformacje podłoża emulsji fotograficznej
Używane jako nośniki emulsji światłoczułej błony acetanowe i poliestrowe, pod wpływem temp., wilgotności i czasu składowania kurczą się. Uwzględnić je można przez porównanie pomierzonych odl. znaczków tłowych z ich nominalnymi wartościami. Pozwala to określić i uwzględnić deformację podłoża o charakterze afinicznym.
Wpływ niepłaskości emulsji fotograficznej
Emulsja nie stanowi idealnej płaszczyzny. Gdy emulsja odstaje od płaszcz. ramki tłowej, to promień utworzy obraz w punkcie na powierzchni emulsji, zamiast być odwzorowany w punkcie płaszcz. tłowej. Dalszemu pomiarowi podlega punkt, który jest rzutem ortogonalnym obrazu na płaszczyznę. W wyniku tej niepłaskości następuje radialne przesunięcie punktów zdjęcia względem ich położenia zgodnie z zasadą rzutu środkowego.
Wpływ refrakcji atmosferycznej
Promienie świetlne tworzące obraz fotograficzny, nie rozchodzą się po liniach prostych, lecz się załamują, gdy przechodzą przez warstwy powietrza o różnej gęstości. Wartość kątową tego przesunięcia nazywamy refrakcją atmosferyczną. Wielkość refrakcji zależy od stanu atmosfery. Wpływ refrakcji rośnie ku skrajom zdjęcia
Wpływ krzywizny Ziemi
Zakrzywienie Ziemi nie powoduje zniekształceń wiązki perspektywicznej. Jednak współrzędne geodezyjne są odniesione do przyjętej płaszczyzny odwzorowawczej, więc trzeba uwzględnić zakrzywienie Ziemi.
Aby przedstawić pow. Ziemi na płaszczyźnie, należy wprowadzić poprawkę radialną, do pomiarów na zdj. Wpływ krzywizny Ziemi rośnie szybko ku skrajom zdj., jest wprost proporcjonalny do wys. fotografowania i odwrotnie proporcjonalny do odległości obrazu.
ZNIEKSZTAŁCENIA OBRAZU
(Dystorsja, błędy szczątkowe obiektywu, deformacja podłoża, deformacja sensora cyfrowego, refrakcja fotogrametryczna, krzywizna ziemi)
A) Dystorsja - Jej eliminacja oparta jest na wykorzystaniu wielomianów. Krzywą dystorsji radialnej opisuje wielomian:
Δr= a0r+a1r3+a2r5+a3r7+... gdzie a- wsp. Określający kształt krzywej
Promienie radialne dla zdjęcia prawego i lewego ![]()
B) Szczątkowe wady obiektywów (aberracje, astygmatyzm) są we współczesnych obiektywach praktycznie zaniedbywalne
Korekcja współrzędnych tłowych zdjęcia
Δrx' = x' (k0 + k1r'2 + k2r'4 + k3 r'6 + ...)
Δry' = y' (k0 + k1r'2 + k2r'4 + k3 r'6 + ...)
Gdzie![]()
C) Deformacja podłoża - np. błona negatywu może nie przylegać do płytek, lub uległa deformacji w procesie niewłaściwego przechowywania lub obróbki (podobnie obróbka diapozytywów) mogą powodować miejscowe zniekształcenie obrazu
Eliminacja w procesie transformacji afinicznej (z wyrównaniem deformacji przypadkowych)
D) Deformacja sensora cyfrowego może powodować szumy obrazów cyfrowych. Eliminacja - filtr dolnoprzepustowy, medianowy
E) Refrakcja fotogrametryczna powoduje zwiększenie się promienia ra przy wykonywaniu zdjęć dużych wysokości. Promienie świetlne przechodzą przez warstwy powierzchni o różnej gęstości,
są odchylone (punkty przesuwają się na zewnątrz od pkt. główn.) jest to zniekształcenie radialne (w punkcie nadirowym = 0) jego wielkość wzrasta wraz ze wzrostem W i kąta α. Zarówno wpływ
refrakcji jak i krzywizny ziemi uwzględnia się przy precyzyjnych opracowaniach zdjęć lotniczych.
F) Krzywizna ziemi powoduje zmniejszenie promienia ra jest to zniekształcenie zmniejszające wymiary obrazu, przesuwające obraz punktów terenowych w kierunku punktu nadirowego.
Poprawki można wprowadzać do poszczególnych zdjęć lub modeli.
Zniekształcenie Δr proporcjonalne do wysokości lotu W, wielkość promienia radialnego r, odwrotnie proporcjonalna do Ck
8. ORIENTACJA WEWN. - to wyznaczenie parametrów, które pozwalają odtworzyć bieg prom. w kamerze.
Elementami orientacji wewnętrznej kamery są:
-stała kamery ck.
-położenie punktu głównego zdjęcia w ukł. wsp. tłowych x0 y0
Elementy uzyskujemy w procesie kalibracji (negatywy x0=0 y0=0 z0=f, pozytywy x0=0 y0=0 z0=-f,)
Zdjęcie fotograficzne jest rzutem środkowym. Ważna jest precyzja rekonstrukcyjna tego rzutu. Rekonstrukcji tej dokonuje się na drodze graficznej, matematycznej. Elementy orientacji wewn. pozwalają na zrekonstruowanie wiązki promieni podobnej do tej, jaka była w momencie fotografowania. Elementy orientacji wewn określają położenie wewn. środka rzutów Ot w odniesieniu do płaszczyzny ramki tłowej. Są to:
*odl.środka rzutów od płaszczyzny tłowej, zwana odl. obrazowa kamery Ck,
*położenie punktu głównego O' (w ukł. wsp. tłowych), który jest punktem przebicia płaszczyzny tłowej prosta przechodzącą przez środek rzutów Ot i prostopadłą do płaszczyzny tłowej. Punkt ten nazywa się punktem głównym O'(xo,yo)
Dla zdjęć fotogrametrycznych, gdy odl. fotografowania jest na tyle duża, że obraz powstaje w płaszcz. ogniskowej, odl. środka rzutów od płaszczyzny tłowej jest równa, ogniskowej kamery.
Punkt glówny O' wyznaczony jest przez przecięcie się linii łączących przeciwlegle znaczki tłowe, umieszczone odpowiednio w płaszczyźnie tłowej kamery i odfotografowanie na zdjęciach.
9. EFEKT STEREOSKOPOWY
Obserwacja dwuoczna, która pozwala na spostrzeżenie głębokości (odległości) nazywa się stereoskopowym widzeniem. Powstanie efektu stereoskopowego wynika ze zdolności człowieka do przestrzennego widzenia.
Z geometrycznego punktu widzenia, jednoczesna obserwacja dwuoczna jest przestrzennym wcięciem obserwowanego punktu z końców bazy danych. W stereofotografii takie przestrzenne wcięcie w przód, realizowane jest przez fotografowanie tego samego obiektu z dwóch końców bazy. Końcami bazy fotografowania są środki rzutów obiektywu kamery pomiarowej w momentach wykonywania zdjęcia.
Podstawą tworzenia obrazu stereoskopowego jest równoczesna obserwacja tego samego obiektu z dwóch końców bazy. Jeżeli posłużymy się dwoma aparatami fotograficznymi to promienie przechodzące przez skrajne punkty przedmiotu utworzą dwie płaszczyzny zdjęć. Różnica długości jednoimiennych odcinków nazywane jest paralaksą liniową.
Metody uzyskania sztucznego efektu stereoskopowego.
W celu uzyskania sztucznego efektu stereoskopowego należy zapewnić jednoczesną lecz rozdzielną obserwację zdjęcia, lewego, lewym okiem i prawego, prawym.
Uzyskuje się to przy pomocy :
*stosowania ukł. optycznych umożliwiających stereoskopowe widzenie: stereoskopy, stereokomparatory, autografy.
*Metoda anaglifowa - równoczesna obserwacja obu zdjęć w barwach dopełniających przez ukł. optyczny zaopatrzony w odp. filtry. Pomiary wykonuje się metodą rzeczywistego znaczka pomiarowego.
*Metoda wirujących przesłon - naprzemienna projekcja lewego i prawego zdjęcia. Pomiary wykonuje się metodą rzeczywistego znaczka pomiarowego.
*Metoda polaroidów - rozdzielenie obrazów lewego i prawego zdjęcia poprzez spolaryzowanie wiązek rozświetlających w kierunkach prostopadłych (każde oko uzbrojone w odp. polaryzator). Model uzyskujemy w barwach rzeczywistych.
*Metoda rzeczywistego znaczka pomiarowego - dwie pary zwierciadeł z których wewn. są półprzepuszczalne. Na tle pozornego modelu obserwator uzyskuje rzeczywisty znaczek pomiarowy. Znaczek ma możliwość ruchu w trzech płaszczyznach, ruch odczytujemy na podziałkach. Wadą jest możliwość kątowego zniekształcenia modelu, środki projekcji są środkami soczewek.
*Metoda pozornego znaczka - 2 znaczki umieszczone w płaszcz. zdjęć tworzą obraz pozornego znaczka tłowego w przestrzeni. Ruch jednego ze znaczków w kierunku równoległym do osi x daje wrażenie ruchu pionowego pozornego znaczka pomiarowego
Aby uzyskać sztuczny efekt stereoskopowy ze zdjęć fotograficznych należy spełnić następujące warunki:
1.Zdjęcia muszą być wykonane z dwóch stanowisk
2.Obydwa zdjęcia powinny być wykonane w podobnej skali - nie różniącej między sobą więcej niż 16%.
3.Każde oko powinno obserwować odpowiednie zdjęcie.
4.Zdjęcia powinny być obserwowane w płaszczyźnie rdzennej (która zawiera obydwa środki rzutów S1 i S2 i dowolny punkt A)
5.Promienie rzutujące zdjęć nie mogą przecinać się pod kątem >15°-wynika to ze stosunku bazy ocznej (bo= ok.65mm) do odl. najlepszego widzenia (Ymin= ok. 250mm). Przy odl. <Ymin następuje zanikanie stereoskopowego widzenia, a kąty osi optycznych oczu są wtedy >15°.
6.Prowadzenie obserwacji zdjęć z odległości najlepszego widzenia.
Dzięki pomiarom stereoskopowym uzyskana dokładność jest 1,8 x większa niż przy pomiarach monekularnych.
WIDZENIE PRZESTRZENNE
Oczy człowieka znajdują się w stałej od siebie odległości zwanej bazą oczną bo= odległości między środkami obrotu oczu S' i S” [bo=(58-72mm)]. W przypadku obserwowania bardzo odległych obiektów (np. gwiazdy), osie optyczne oczu S'O' i S”O” są do siebie równoległe i prostopadłe do bazy. Obraz gwiazdy otrzymamy w p-ktach główn. oka lewego i prawego. W skutek tego obydwa obrazy zleją się w mózgu w jeden przestrzenny p-kt do którego odl. nie sposób określić, bo przecięcie osi optycznych następuje w nieskończoności. Z tego względu wszystkie gwiazdy wydają się być jednakowo oddalone od obserwatora. Jeżeli obserwujemy punkty w odl. skończonej, to osie optyczne są zbieżne (konwergentne). Ponieważ baza oczna jest mała, wcięcia otrzymujemy pod ostrym kątem, więc określenie odl. jest mało dokładne (rzędu 10-20%). Jeżeli dowolny punkt będzie znajdował się w odl. mniejszej od maks głębokości (odl.) widzenia osie oczu zbiegające się w tym punkcie utworzą kąt paralaktyczny zwany też paralaksą kątową. Jej wielkość także odbierana jest przez obserwatora w sposób przybliżony. Dopiero różnica dwóch paralaks kątowych percypowana jest o wiele dokładniej i na jej podstawie możemy określić wzajemne rozmieszczenie punktów w przestrzeni. Różnica ta wywołuje u obserwatora tzw paralaksę fizjologiczną, powodującą odczucie wzajemnego przestrzennego rozmieszczenia punktów obserwowanych (głębokość).
Stereogram lotniczy
Stereogram lotniczy tworzy para zdjęć lotniczych wykonanych w podobnej skali (różnica do 16%), które mają zwykle pokrycia wzajemne około 60% ich powierzchni.
Rodzaje efektu stereoskopowego
W zależności od ułożenia zdjęć względem siebie może być uzyskany jeden z trzech rodzajów efektu stereoskopowego:
- efekt ortoskopowy - przy którym model utworzony z pary zdjęć lotniczych ma ukształtowanie pionowe zgodne z naturalnym tzn. wzniesienia terenowe są skierowane w stronę obserwatora. Bazy fotografowania zajmuje położenie „do wewnątrz”.
- efekt pseudoskopowy - przy którym następuje zmiana ukształtowania pionowego, tzn. formy wypukle obserwuje się jako wklęsłe, rzeki płyną grzbietami itp. Powstaje na skutek obserwacji zdjęcia lewego prawym okiem, a prawego lewym. Baza fotografowania na zdjęciach zajmuje położenie „na zewnątrz”.
- efekt zerowy - (minimalny), przy którym zanika wrażenie plastyki. Teren plaski. Zdjęcie lewe skręcone jest o 90o i obserwowane lewym okiem, a prawe jest także skręcone o 90o i obserwowane prawym okiem. Efekt zerowy stosowany jest wtedy, gdy przy obserwowaniu stereogramu niepożądana jest obserwacja przestrzennego ukształtowania terenu.
10. UKŁ. WSP. STOSOWANE W FOTOGRAMETRII
*ukł. wsp. tłowych - jest to prawoskrętny ukł. ortogonalny, którego początek to środek rzutów a pł. zdjęcia to x'y'. Przyjmuje się prostopadłość osi kamery w punkcie gł. O', ukł. odniesienia jest przesunięty do płaszczyzny zdjęcia. Środek rzutów ma tu wsp. (xo'yo'ck). Często początek ukł. jest przesuw. do środka rzutów O, wtedy zdjęcie można rozpatrywać w położeniu negatywowym (czyli położenie kamery podczas fotografowania) i pozytywowym, dla którego jest zgodność zwrotów osi układu. W obu przypadkach te same punkty będą miały te same współrzędne x=xn, y=yn przy czym trzecia z=zn=-ck ma wartość ujemną ze względu na przeciwne kierunki osi z oraz osi kamery. W przypadku zdjęć naziemnych oś kamery ma ten sam zwrot co oś układu terenowego Y i dlatego wartość ck (odległość obrazowa) jest dodatnia.
* ukł. wsp. tłowych płaski
* ukł. wsp. tłowych przestrzenny (x',y', +- Ck=z')
* ukł. wsp. transformowanych (ukł. wsp. tłowych zdjęcia po obrocie o kąty fi, kappa, omega, po którym osie są równoległe do osi lokalnego układu współrzędnych)
* ukł. wsp. terenowych: XYZ definiowany jest jako prawoskrętny ukł. ortogonalny, Zazwyczaj oś X jest zgodna z kier osi szeregu, Początek może być dowolny ale zazwyczaj obierany jest w środku obszaru. Dla osi Z dodatni kierunek zwrotu, w tym ukł. są przedstawione ostateczne wyniki opracowania dzięki znajomości wsp. punktów osnowy odwzorow. na zdjęciach. W tym układzie wiązka homologiczna jest definiowana elem XoYoZo i fi ksi.
- ukł. wsp. geodezyjnych z szerokością geod. B, dł. geod. L i wys. nad elipsoidą odniesienia H. Jest ściśle związana z elips. odnieś.
- ukł. geocentryczny - początek w środku masy ziemi, płaszcz. równika przechodzi przez początek ukł. i jest prostopadła do osi Z , oś X przechodzi przez południk Greenwich , a oś Y leży na 90° dł. wschodniej w układzie prawoskrętnym.
- lokalny ukł. wsp. XYZ - prawoskrętny ukł. przestrzenny. Za początek można przyjąć dowolny fotopunkt lub inny dogodny punkt. Oś Z jest prostopadła do elipsoidy, a osie X i Y są równoległe do płaszcz. stycznej do elipsoidy. Oś Y pokrywa się z kierunkiem północy, a za początek wys. przyjmuje się p-kt poniżej powierzchni, ażeby wszystkie punkty terenowe miały wartości dodatnie.
* ukł. wsp. modelu - odnosi się do wsp. punktów zobrazowanych na modelu stereoskop. i ustalonych analitycznie lub analogowo na autografie. Prawoskrętny ukł. ortogonalny. Początek w środku rzutów lewego zdjęcia. Kierunek osi X pokrywa się z kierunkiem bazy zdjęcia (lub kierunkiem lotu), oś Y jest równoległa do osi y zdjęcia w położeniu negatywowym.
* ukł. wsp. pikselowych - standardowo może być zdefiniowany tak, że początek ukł. wsp. jest w lewym górnym rogu matrycy
-jest prostokątny więc trzeba uwzględnić jego wymiar przy przejściu od układu współrzędnych pikselowych na układ tłowy
* ukł. wsp. fotogrametrycznych (zdjęcia naziemne) -to pierwszy etap wyznaczania wsp. terenowych. Używa się go w stereogrametrii naziemnej tzw. terenowy ukł. ortogonalny związany z osią kamery pomiarowej XF,YF,ZF.
Transformacje
W przestrzeni euklidesowej
Afiniczna
Rzutowe płaszczyzny
Rzutowe przestrzeni na płaszczyznę
Transformacje na płaszczyźnie (afiniczne)
Translacja to przesunięcie obrazu o wektor. Jednemu punktowi na płaszczyźnie przyporządkowany są jednoznacznie inne punkt. Translacja można potraktować jako jako transformację współrzędnych z jednego układu na drugi.
![]()
Obrót
α- kąt obrot
Symetria osiowa
Względem osi X :x'=x, y'=-y
Względem osi X :x'=-x, y'=y'
Symetria środkowa
Jednokładność o środku O i skali k punktowi P przyporządkowuje punkt P' taki że odcinek OP= k*OP' x'= k* x ,y'= k* y
Powinowactwo- zmiana skali wzdłuż osi jest różna ,
np. x'=x, y'=k*y
Przekształcenia afiniczne to wzajemnie jednoznaczne przekształcenia na płaszczyźnie ; jest to przekształcenie liniowe każde dwie linie równoległe przechodzą w proste równoległe , nie zachowana jest tylko odległość
X'=ax+by+c
Y'=dx+ey+f
Przekształcenie rzutowe płaszczyzny na płaszczyznę:
Przekształcenie rzutowe przestrzeni na płaszczyznę:
![]()
![]()
Redukcja wsp. tłowych zdjęcia i pikselowych obrazu
x0,y0 - określa położenie środka rzutów w stosunku do układy współrzędnych tłowych na zdjęciu
xa = xa' - x0, ya = ya' - y0
w procesie transformacji afinicznej dokonuje się redukcji wsp. tłowych i korekcja błędów systematycznych (min. 3 pkt dostosowania, najpierw odległość wsp. transformowanych, potem przeliczane są współrzędne)
Przejście z ukł. piks. do tłowego x' = (X'-Xp')px x' = (Y'-Yp')py
Transformacja pomierzonych wsp. piksel. do ukł. wsp. tłowych za pomocą transformacji afinicznej w VSD
Metody transformacji wsp. tłowych zdjęcia i piksel. obrazu
Deformacje spowodowane są tym, że nie zachowana jest oś odciętych, rzędnych przy skanerze. Otrzymujemy układ z nieprostopadłymi osiami, wówczas trzeba stosować transformacje, które powodują:
- redukcję układu
- wprowadzenie korekcji deformacji ze wzgl. na błędy systematyczne podłoża fotograficznego (najczęstszym źródłem błędów systematycznych jest niedociskanie materiału fotograficznego w momencie ekspozycji oraz zniekształcenie spowodowane jego obróbką i przechowywaniem)
- największa jest deformacja materiału negatywowego
- błędy szczególne układu optycznego kamery fotograficznej (deformacja radialna i tangencjalna)
Do wprowadzenia korekcji systematycznych błędów wsp. tłowych stosuje się transformacje, które przekształcają pomierzone wsp. tłowe na układ wsp. wzorcowych
Sytuacja: mamy 4 znaczki tłowe i obserwując wsp. tłowe jesteśmy w stanie ułożyć 8 równań:
1. transformacja przez podobieństwo (konforemna) transformacja Helmerta - zachowuje kąty w skali. Mamy do wyznaczenia 4 wsp, które opisują model korekcji tak, że musimy mieć 2 znaczki tłowe z pomierzonymi wsp tłowymi z uwzględnieniem kalibracji kamery. Możemy wtedy ułożyć 4 równania obserwacyjne rozwiązać je metodą podstawienia i wyznaczyć niewiadome: a0, b0, a, b. Zakładamy tu, że: osie układu są ortogonalne, zniekształcenia skali wzdłuż obu osi są jednakowe (2 pkt dostosowania)
x' = a0 + a1xs' - b1ys'
y' = b0 + b1xs' - a1ys' xs', ys' - w układzie stereokomparatora
2. pseudoafiniczna (bilinearna) - musimy wyznaczyć współczynnik, stąd potrzeba 4 znaczków tłowych. Stosowanie metod ścisłych jest utrudnione, ponieważ brak tu obserwacji nadliczbowych, tzn ukł. równań jest słabo określony. Transformacja ta nie powinna być stosowana w przypadku kamer z 4 znaczkami tłowymi, najlepiej stosować ją dla kamer semimetrycznych ... ponieważ tutaj jest dużo obserw. nadliczbowych.
x' = a0 + a1xs' + a2ys' + a3xs'ys'
y' = b0 + b1xs' + b2ys' + b3xs'ys'
3. afiniczna - zakłada wyznaczenie 6 wsp. opisujących ten model transformacji. Musimy tu mieć 3 znaczki tłowe i na ich podst. ułożyć 6 równań poprawek dla współczynnika. Dzięki niej można obliczyć mx, my (wsp. zmiany skali wzdłuż osi) oraz kąty między osiami ukł. Metoda uwzględnia nieprostopadłość osi ukł. i różnoskalowe zniekształcenia wzdłuż osi ukł. wsp. Mimo, że nie zachowuje kształtu, linie równoległe po transformacji pozostają równoległe. Oprócz poprawienia skurczu za pomocą wsp skalujących, transformacja poprawia również przesunięcie początku ukł. wsp. z ukł. wsp. komparatora xs, ys do ukł. wsp. tłowych zdjęcia x, y oraz stosuje obrót o kat skręcenia obydwu układów.
x' = a0 +a1xs' + a2ys' + a3xs'ys'
![]()
y' = b0 + b1xs' + b2ys' + b3xs'ys' => x' = x0 + Rx'
Etapy: I - określenie współczynników a i b wykorzystując p-kty, które znane są w obydwu układach
II - przeliczenie wszystkich p-któw z ukł. xs, ys na układ x, y wykorzystując obliczone współczynniki. W celu wprowadzenia poprawek można napisać 2 równania typu (wyżej) dla każdego znaczka tłowego, czyli dla 4 znaczków tłowych 4 równania Mz wsp. x i 4 dla y. Dla określenia współczynnika a potrzeba tylko 3 równań dla wsp. x, podobnie jak dla współczynnika b wystarczają 3 równania Mz wsp. y. Równoczesne rozwiązanie tych równań met. najmniej. kwadratów zwiększa dokł. wyznaczanych niewiadomych.
11. ORIENTACJA ZEWNĘTRZNA
Elem. orient. zewn. wsp. środka rzutów S w ukł. wsp. prostokątnych X0, Y0, Z0 oraz kąty:
ω- kąt zawarty między osią kamery a jej rzutem na płaszczyznę poziomą (nachylenie poprzeczne osi kamery).
ϕ- kąt zwrotu, zawarty pomiędzy rzutem poziomym osi kamery a kierunkiem do znanego punktu (nachylenie podłużne )
χ- kąt skręcenia zdjęcia w płaszczyźnie własnej
Mając elem. orient. wewn. można zrekonstruować wiązkę promieni jaka w momencie naświetlania utworzyła obraz w kamerze, natomiast położenie tej wiązki w trójwymiarowej przestrzeni wyznacz się za pomocą sześciu elem/ orientacji zewnętrznej.
PRZEKSZTAŁCENIE RZUTOWE
x=a11(X-X0)+a12(Y-Y0)+a13(Z-Z0), y=a21(X-X0)+a22(Y-Y0)+a23(Z-Z0),
z=a31(X-X0)+a32(Y-Y0)+ a33 (Z-Z0),
X =t*x', y = t*y' , z = t*z'→ x' = (1/t)*x, y' = (1/t)*y, z' = (1/t)*z,
w naszym przypadku z' = -ck, czyli -ck = (1/t)*z →(1/t)*c = ck/z, skąd x' = -ck (x/z) i y' = -ck(y/z) ↔ x' = -ck { [a11(X-X0)+a12(Y-Y0)+a13(Z-Z0)] / [a31(X-X0)+a32(Y-Y0)+a33(Z-Z0)]}
y' = -ck { [a21(X-X0)+a22(Y-Y0)+a23(Z-Z0)] / [a31(X-X0)+a32(Y-Y0)+a33(Z-Z0)]}
12. ORIENTACJA WZAJEMNA STEREOGRAMU
Ma na celu doprowadzenie pary zdjęć do takiego położenia jakie zajmowały one w momencie naświetlenia. W takim położeniu bowiem promienie jednoimienne należące do dwóch wiernie zrekonstruowanych wiązek, przecinają się tworząc model optyczny podobny do przedmiotu. Orient. wzaj. dokonuje się tylko wtedy gdy nie znane są elementy o. zewn. Do jej przeprowadzenia wymagany jest pomiar 6 punktów (5 elementów = 5 równań+1 równanie do wyrównania). Elem. orient. wzaj. można zdefiniować w różny sposób w zależności od przejętych warunków początkowych.
Elem. orient. wzaj. pozwalają na odtworzenie wzajem. położenia pary zdjęć tworzących stereogram.
Ukł. umownie poziomej bazy (zdjęcia niezależne) Δω, ϕ`,ϕ``,χ`,χ``
Ukł. umownie poziom. zdjęcia (zdjęcia zależne) by, bz, Δω, Δϕ,Δχ
by - rzut bazy na oś y
bz - rzut bazy na oś z
bx - nie jest tu istotny, ma wpływ tylko na skalę modelu.
Δϕ - różnica kątów nachylenia podłużnego, określona w płaszczyźnie x2 z2
Δω - różnica kątów nachylenia poprzecznego, określona w płaszczyźnie y2 Ck
Δχ - różnica kątów skręcenia, określona w płaszczyźnie drugiego zdjęcia
Metoda Schuta (analityczna)
Met. tą realizuje się gdy ukł. jest zdefiniowany tu umownie B x rI . rII = 0 pozornym lewym zdjęciem. Początkowo punkty przestrzeni przedmiotowej powinny znajdować się w płaszczyznach rdzennych (komplanarność). Na początku zakladamy tu dla lewego zdjęcia, że I, I,I = 0, poprawki dla wsp. tłowych xI , xII = 0 , natomiast poprawki dla yI , yII różnią się znakami, a więc redukują się
Niewiadomymi w równaniu są: by, bz i wsp. xII, yII, zII będące wsp. promienia rzucającego rII ,określonymi pomierzonymi na zdjęciu wsp. xII, yII oraz ck II, II II Dlatego poszukiwanymi niewiadomymi są by , bz, II, II II.
KOLEJNOŚĆ OBLICZEŃ (musimy tu mieć min 5 punktów )
1. Ze znanych lub przyjętych dla pierwszego zdj. obrotów tworzymy macierz obrotów A i określamy następnie wielkości xiI, yiI, ziI wsp. wektora rI .
2. Wybieramy wartości przybliż. dla drugiego zdj. by , bz, II, ϕII II.
3. Obl. wartości xII, yII, zII za pomocą wartości przybliż. (w p-kcie. 2)
4. Obl. niewiadome d d d dbz dby przez rozwiązanie min5 równ.
5. Obl. pierwszej poprawionej macierzy 2A posługując się elem. obl. w punkcie.4
6. Obl. macierz A = 2A . 1A. Elem. tej macierzy posłużą do nowych obliczeń jak w punk. 3
7. Powtarzamy obl. od punk.3 do 6 dopóki d, d, d, dbz , dby nie staną się dostatecznie małe aby je pominąć
Pięć p-któw musi być rozmieszczone jak przy p-ktach standardow., ze wzgl. na powierzchnie krytyczne. Gdy mamy więcej niż 5 p-któw niewiadome (pun.4) obliczamy z wyrównaniem. Równania błędów rozwiązujemy metodą najmniejszych kwadratów.
13. ORIENTACJA BEZWZGLĘDA MODELU
7 Elem. orient. bezwzgl.: 3 el liniowe x0, y0, z0, 3 elementy katowe ω,φ,χ; oraz współczynnik zmiany skali λ
Do skalowania modelu potrzebne są 2 punkty o znanych wsp. geo.
Orient. bezwzgl. polega na odpowiednim obróceniu modelu w ten sposób, aby zajął on takie samo położenie wzgl. poziomu, jakie zajmuje teren odwzorowany na zdjęciach.
Polega ona na przetransformowaniu ukł. lokalnego (ukł. wsp. modelu) do ukł. wsp. terenowych, czyli doprowadzeniu modelu do założonej skali i poziomu, gdyż model uzyskany w wyniku orient. wzajemnej nie ma skali i ma przypadkowa orientacje w przestrzeni. Początkiem lokalnego ukł. wsp. jest środek rzutów lewego zdjęcia a oś celowa lewego zdjęcia pokrywa się z osią ukł. wsp. Zależność między tymi dwoma ukł. opisana jest wektorami. Wektor x0 opisuje odl. wektorową między ukł. wsp. geodezyjnych a środkiem rzutów ukł. wsp. modelu; wektor xS opisuje położenie punktu w ukł. wsp. geodezyjnych, a wektor x - w ukł. modelu.
Sposób zapisu wcięcia w przód: xS=x0+λRx
Otrzymujemy tu zespół równań z 7 parametrami transformacji x0, y0, z0 (składowe przesunięcia wektora translacji) elementy kątowe φ, ω, χ macierzy obrotu oraz wsp. zmiany skali λ. Może być tak, że współczynnik zmiany skali wzdłuż każdej osi jest inny (λx, λy, λz) i wtedy mamy 9 niewiadomych
Jednak najczęściej stosuje się 3 pełne fotopunkty, z czego można ułożyć 9 równań. Układ poprawek rozwiązujemy metodą najmn. kwadratów i w konsekwencji otrzymujemy parametry transformacji przestrzennej. Parametry te otrzymujemy w procesie iteracyjnym. Teraz korzystając z tych równań obliczamy x, y, z, każdego punktu, który nie jest w danym modelu fotopunktem.
14. AEROTRIANGULACJA METODĄ WIĄZEK
Aerotriang. - służy do wyznaczenia wsp. przestrzennych p-któw (x, y, z) na drodze analitycznej lub analityczno-numerycznej na podst. pomierzonych na zdjęciu wsp. tłowych. Punkty te będą punktami zagęszczenia osnowy III klasy lub osnowy pomiarowej. Jednocześnie służy do wyznaczenia punktów dowiązania w procesie orientacji bezwzględnej modelu.
Za pomocą aerotriangulacji wyznaczamy również elementy orientacji zewnętrznej.: Xo, Yo, Zo , , ϕ, χ
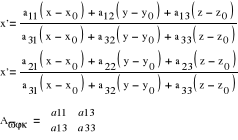
A , ϕ, χ macierz obrotu
Metody aerotriangulacji:
*metoda etapowa (niezależnych modeli)
*metoda wiązek
Sieć budowana jest jednocześnie ze wszystkich zdjęć szeregu lub bloku. Od razu wyznaczamy wsp XYZ i wyznaczamy el. o . zew.
Piszemy równania wiązek:
1. Jeżeli mamy fotopunkt (czyli punkt o znanych wsp. tłowych i terenowych):
X=x' Y=y' Z=-Ck
To równanie wiązek ma postać: ![]()
A- macierz obrotu
![]()
Lub układamy takie równania:
Piszemy więc 18 równań ( 3*6- 3równania dla 6 punktów)
2. Jeżeli mamy punkt wiążący o znanych współrzędnych tłowych
Proste z dwóch zdjęć prowadzone ze środków rzutów powinny się przeciąć. Prosta l1 i l2 muszą mieć jeden punkt wspólny -punkt P
![]()
Układa się takie same równania dla Y i Z
Niewiadome to x, y, z oraz elementy orientacji zewnętrznej. Met. wiązek to metoda jednoetapowa. Pisze się równania i rozwiązuje. Równania tworzy się na podst. kolinearności równań. Przy tej met. potrzebne są: zdjęcia ,osnowa, punkty wiążące, fotopunkty
Cechy metody wiązek:
istnieje możliwość dołączenia obserwacji geodezyjnych (np. pomierzonych dł. między fotopunktami, obserwacji różnic wys., pomierzone azymuty, pomierzone kierunki) co czyni ukł. równań lepiej rozwiązywalnym,
można przyjąć do wyrównania obserwacje fikcyjne np. obserwacje zbiornika wodnego, przyjmujemy że powierzchnia wody jest w każdym punkcie taka sama,
możemy też wprowadzić dodatkowe parametry opisujące błędy systematyczne zdjęcia (dystorsja radialna, tangencjalna, deformacja negatywu). Można je opisać w postaci wielomianu
Minusy:
problem nieliniowości (trzeba linearyzować równania poprawek)
wymaga pracochłonnych metod obliczeń wartości przybliżonych dla wszystkich niewiadomych,
jest to metoda o dużym nakładzie obliczeń,
stanowi rozwiązanie przestrzenne, a więc nie jest możliwe rozdzielenie wyrównania sytuacyjnego i wysokościowego.
Plusy:
najdokładniejsza metoda rozwiązania aerotriangulacji dzięki temu, że zachodzi bezpośredni związek między wsp. zdjęcia a wsp. geodezyjnymi, wyrównanie przez równanie kolinearności (nie ma konieczności rozwiązania pojedynczego modelu jako etapu obliczeń)
jest możliwość wprowadzenia dodatkowych obserwacji geodez.,
możliwość prowadzenia obserwacji GPS dla elem. orient. zewn.
wprowadzenie obserwacji fikcyjnych (obserwacje np. punkty leżące na jednej prostej - linia przesyłowa wysokiego napięcia na wybranym odcinku),
możemy wprowadzić parametry dodatkowe opisujące błędy systematyczne kamery,
pozwala wyznaczyć obraz rastrowy dla autografów analitycznych i cyfrowych (bo otrzymujemy elem. orient. zewn. zdjęć),
pozwala rozwiązać zdjęcia o niekonwencjonalnych orientacjach
15. AEROTRIANGULACJA METODĄ NIEZALEŻNYCH MODELI
To rozwinięcie metody wyznaczania XYZ przez orient. wewn., wzajemną, bezwzględną
Tworzymy tu tyle niezależnych modeli ile mamy stereogramów.
Modele są niezależne bo mają różne układy współrzędnych. Trzeba wiec przetransformować je do jednego układu wspólnego. A więc mamy etapy: - modele - transformacja niezależnych modeli do wybranego ukł. wsp. Model transformowany jest do układu geodezyjnego w oparciu o wsp. fotopunktów. W procesie tym należy pomierzyć wsp. tłowe: fotopunktów (min 3), punktów wiążących i punktów nowo wyznaczanych. Niewiadomymi w tej metodzie są elem. orient. bezwzgl. (razy ilość modeli) i wsp. terenowe punktów wiążących.- orientacja bezwzględna modelu. Przy tej met. potrzebne są: zdjęcia ,osnowa, punkty wiążące, fotopunkty
Dokładność aerotriangulacji:
Oceniamy xyz punktów wyznaczanych. Rozplanowujemy jak rozmieścimy fotopunkty (do zaplanowanej liczby dodajemy jeszcze 50% - posłużą one do wyrównania, kontroli, wyliczenia błędów)
Dokł. wyznaczenia xyz oraz el. orient. zewn. zależy od tego jak została wykonana o. wewn. Jak dokładnie wyznaczyliśmy punkty wiążące, od dokładności pomiaru fotopunktów.
Większy wpływ ma błąd identyfikacji p-ktu na zdjęciu niż w terenie
17. TEORET. PODST. SPASOWANIA - MATCHING Matching- metoda spasowania obrazow pozwalajaca na zautomatyzowanie wyznaczenia współrzędnych pikselowych punktow homologicznych. Metody matchingu obrazu: 1. Area Based Matching- bazuje glownie na analizie odcieni szarości w danym fragmencie obrazu, porównywanie pikseli na jednym i drugim obrazie. W przypadku obrazu kolorowego analizuje się jedna ze składowych RGB( R- intensywność barwy czerwonej; G- barwy zielonej, B- barwy niebieskiej R+G+B/3) lub analizuje się wagowana kombinacje składowych. W metodzie tej sadwarozne sposoby: m. korelacji, m. najmniejszych kwadratow. 2. Feature Based Matching- porównaniu podlegaja cechy obrazu (punkty, krawędzie obiektow, poligony). Wyodrębnienie krawędzi odbywa się na podstawie filtrow. 3. Symbolic Matching- stosowany do automatycznego pomiaru znaczkow tlowych.
AEOROTRIANGULACJA CYFROWA - wykorzystuje korelacje obrazów. 1) met. półautomat. gdzie operator interaktywnie wybiera 1 p-kt wiążący w pobliżu nominalnego poł. w pasie pokrycia zdj. P-kt ten transferowany jest met. „image matching” na wszystkie zdj. na których występuje. Np. Photo-T zainstalowany na Image Station INTERGRAPH 2)met. automat. gdzie p-ty wiążące są automat. wybierane, transferowane i mierzone w 9 nominalnie rozmieszczonych oknach.
18. NMT
Numeryczny Model Rzeźby Terenu (Digital Terrain Model - DTM) jest numeryczną, dyskretną (punktową) reprezentacją wys. topograficznej powierzchni terenu, wraz z algorytmem interpolacyjnym umożliwiającym odtworzenie jej kształtu w określonym obszarze. Zwykle DTM jest reprezentowany przez punkty, rozłożone regularnie lub nieregularnie na powierzchni terenu uzupełnione dodatkowo punktami opisującymi morfologiczne formy terenu.Algorytm interpolacyjny, który jest nieodłączną składową DTM, pozwala określić (wyinterpolować) wartość wysokości dla dowolnego punktu o położeniu określonym przez jego współrzędne x, y, tj. znaleźć wartość z = f(x,y) (w przeciwieństwie do modelowania powierzchni i obiektów w przestrzeni 3D jest to zawsze tylko jedna wartość wysokości). Z pomiarów fotogrametrycznych mamy nieregularną siatkę punktów o znanych współrzędnych X,Y,Z. Za pomocą metod interpolacji budujemy siatkę regularną. Metody:
1Budujemy siatkę trójkątów i na niej rozpinamy powierzchnię - w praktyce są to płaszczyzny.
2W otoczeniu punktu P(Xo,Yo) wyznaczamy współczynniki funkcji Z= f(X,Y) o postaci np.
![]()
3Na punktach siatki rozpinamy krzywe Beziera stopnia trzeciego w obu kierunkach tzn. wzdłuż osi X i Y.
Zagęszczanie siatki regularnej przez interpolację dwuliniową.
Błąd średni wyinterpolowanej wysokości,![]()
mz błąd średni danych pomiarowych, α współczynnik opisujący powierzchnię terenu,
W średnia odległość punktów pomiarowych (długość boku siatki
Punkty reprezentujące DTM mogą być uporządkowane w jednej z dwóch struktur:
-TIN (Triangular Irregular Network) - nieregularna sieć trójkątów wraz z topologią. Wierzchołki trójkątów opierają się na punktach pomiarowych.
-Regularna sieć (kwadratów, prostokątów lub trójkątów) uzupełniona o punkty reprezentujące formy terenowe, takie jak:
linie szkieletowe (grzbiety, cieki),
linie nieciągłości (skarpy, urwiska),
powierzchnie wyłączeń (wody, budynki),
ekstremalne pikiety (wierzchołki, dna).
Regularna sieć (zwykle kwadratów) powstaje zwykle nie poprzez pomiar, lecz poprzez interpolację między rozproszonymi punktami pomiarowymi. Ta sieć jest określana jako „sieć wtórna", lub „sieć wynikowa" DTM.
Z punktu widzenia użytkownika nie jest obojętne jaką strukturę ma DTM. Każda z tych form ma swoje zalety i wady.
Model TIN:
- zachowuje związki topologiczne między punktami pomiarowymi,
- łatwo opisuje i zachowuje w jednakowej strukturze opis morfologicznych form terenowych,
- archiwizacja DTM w tej strukturze wymaga większych zbiorów,
- metody automat. generowania DTM nie przewidują struktury TIN.
DTM w regularnej siatce:
- zawiera dane interpolowane (a nie oryginalne dane pomiarowe),
- daje większą łatwość modelowania powierzchni (interpolacji wysokości w dowolnym punkcie, generowania profili, generowania warstwie, generowania map spadków i ekspozycji, obliczania objętości, określania widoczności między dwoma punktami, łatwiejszą wizualizację 3D powierzchni, łatwiejszą symulację, itd.),
- jest przydatniejszy do generowania cyfrowych ortofotornap, - jest łatwiejszy do archiwizacji (regularna siatka tworzy „macierz" wysokości, określenie struktury tej macierzy pozwala zachowywać dane tylko w postaci współrzędnej „z" węzłów siatki, położenie/węzłów określone jest przez położenie w macierzy).
Doświadczenia pokazują, że pod względem dokładności obie formy są równoważne. Ze względu na łatwość archiwizacji i dalszej obróbki, DTM o krajowym zasięgu budowane są częściej w formie regularnej siatki kwadratów, lub siatki geograficznej.
Dane źródłowe do generowania NMT można uzyskać
-bezpośredni pomiar terenowy
-technologia kartograficzna
-technologia fotogrametryczna, a w tym:
a)opracowanie autogrametryczne
b)opracowanie cyfrowe
c)lotniczy skaner laserowy
d)opracowanie zdjęć i obrazów satelitarnych.
Dokładność
błąd średni wysokości wyinterpolowanej z wynikowego NMT, który składa się z :
-błędów danych pomiarowych
-wielkość oczka siatki determinująca reprezentatywność powierzchni terenu przez węzły siatki NMT
-czynnik opisujący charakter terenu
Przyjmuje się:
a = 0,004 - 0,007 dla terenów łatwych
a = 0,010 - 0,020 dla terenów średnich
a = 0,022 - 0,044 dla terenów trudnych
19. METODA FOTOGRAMETRYCZNA BUDOWY NMT
Fotogrametryczny pomiar zdjęć lotniczych jest najlepszym źródłem danych dla generowania DTM. Pomiar ten może mieć miejsce na: - autografie analitycznym (lub analogowym),
- autografie cyfrowym (cyfrowej fotogrametrycznej stacji roboczej).
Pomiar na autografie (analitycznym czy analogowym) sprowadza się do zbudowania modelu i stereodigitalizacji powierzchni terenu. Pomiarowi podlegają punkty masowe - w miarę regularnie pokrywające obszar - oraz dodatkowo punkty reprezentujące formy terenowe (linie szkieletowe, linie nieciągłości, ekstremalne pikiety, powierzchnie wyłączeń). Autograf analityczny jest bardzo przydatnym narzędziem do tego celu. Dla równomiernego pokrycia obszaru punktami pomiarowymi można realizować pomiar w zadanej siatce (tzw. „siatka pierwotna"), co zwykle ma miejsce. Autograf analityczny pozycjonuje znaczek pomiarowy w wierzchołkach siatki, a operator tylko „stawia znaczek pomiarowy na terenie", co bardzo przyśpiesza pomiar. Możliwy jest pomiar w zadanych profilach, lub „inteligentne" próbkowanie, tj. automat. zmiana gęstości pomiaru w zależności od lokalnego nachylenia terenu. Błąd pomiaru wys. jest wprost proporcjonalny do wys. lotu, z której wykonano zdj. Dla przeciętnych warunków produkcyjnych, przy pomiarze „statycznym" przyjmuje się, że błąd ten wynosi:
MZpoz = 0,1÷0,015%Wf
MZpoz - błąd pomiaru
Wf - wysokość fotografowania
Przyjmuje się, że średnia odległość punktów pomiarowych (oczko „siatki pierwotnej" jeśli pomiar jest realizowany w siatce) jest 2-3 razy większa niż oczko siatki DTM. Oznacza to, że wynikowy DTM zawiera 5-10 razy więcej punktów interpolowanych, niż punktów oryginalnie pomierzonych. W odniesieniu do stereogramu daje to normalnie 2-10 tyś, punktów pomiarowych na stereogram (wielkość zależna od typu terenu, przeciętnie jest to 5-6 tyś. punktów). Zwykle etap pomiaru i etap generowania wtórnej siatki DTM są procesami rozłącznymi w czasie. Zwiększenie oczka siatki DTM poza zalecane powyżej relacje - powoduje obniżenie jego dokładności wysokościowej
20. ORTOFOTOMAPA - METODA GENEROWANIA
Ortofotografia - zdjęcie, którego płaszczyzna projekcji jest równoległa do płaszczyzny odniesienia, a wszystkie promienie są prostopadłe do tych dwóch płaszczyzn. Odległości mierzone na takim zdjęciu są poprawne, niezależnie od różnic wysokości.
Wykonanie ortofotomapy polega na:
-skanowaniu zdjęcie (Zdjęcie zapisywane jest w formacie .bmp .tiff .gif 110MB -zdj. czarno-białe, 330MB -zdj. kolorowe, zdj. posiada rozdzielczość 3880dpi po zeskanowaniu 1300dpi do opracowań fotogrametrycznych)
-odtworzeniu orientacji zewnętrznej zdjęć
-pomierzeniu NMT
-przetworzeniu cyfrowym zdjęć - generowanie ortofotografii
-mozaikowaniu ortofotografii
-redakcji ortofotomapy
-dystrybucji produktu finalnego
Jednym z podstawowych procesów produkcji ortofotomap jest transformacja tablicy zeskanowanego zdjęcia pomiędzy układem kamery i terenowym ukł. wsp. (przepróbkowanie - resampling). Proces ten jest głównym zadaniem w procesie tworzenia cyfrowej ortofotomapy. Definiujemy orto, jej wielkość i zakres w układzie terenowym. Znając rozdzielczość, więc i rozmiar piksela nowego kreowanego rastra, możemy wyznaczyć na podst. oryginalnego zdj. (zeskanowanego) na podst. algorytmu przyporządkowania wartości radiometryczne nowych tworzonych pikseli następującymi metodami:
Najbliższego sąsiada (nearest neighbour) - najprostsza metoda nadająca pikselowi wyznaczanemu wartość radiometryczną taką jak wartość piksela z oryginalnego obrazu, którego środek znajduje się najbliżej wyznaczanego piksela. Wada: W najgorszym przypadku elementy są przesunięte o pół piksela, co powoduje pogorszenie obrazu lini na ortofoto (ząbki). Używając tej metody trzeba brać większą liczbę pikseli do wyznaczenia, by uniknąć tracenia pikseli z oryginału.
Interpolacji dwuliniowej (bilinear transformation) - wartość radiometryczna określana jest na podst. 4 sąsiadujących pikseli. Wartości pikseli są sztuczne i nie odpowiadają jaskrawości realnych obiektów.
Cubic convolution - wartość piksela jest wartością ważoną obliczaną na podstawie 16 otaczających pikseli , przy czym waga jest odwrotnie proporcjonalna do odległości piksela wynikowego.
Wielomianów Langrange'a - Wlk. piksela jest wyznaczana w wyniku interpolacji z 16 najbliższych pikseli
Spline przestrzennych - Wlk. piksela jest wyznaczana w wyniku interpolacji z 16 najbliższych pikseli
21. MOZOIKOWANIE ORTOOBRAZÓW
W wyniku pracy programu Phodis-Op powstają pojedyncze ortofotografie w postaci prostokątów o zdefiniowanej skali i lokalizacji w układzie terenowym. Dla każdego narożnika są znane jego wsp. w ukł. terenowym. Takie produkty stanowią produkt pośredni przy tworzeniu cyfrowych ortofotomap. Wyjątkiem jest przypadek zdjęć celowanych, które z założenia obejmują cały obszar wykonywanej ortofotomapy. Dla tego przypadku na etapie generowania cyfrowej ortofotografii należy określić granice generowania (obszar prostokąta) zgodne z docelowym arkuszem ortofotomapy.
W innych przypadkach na docelową ortofotomapę składa się kilka ortofotografii w całości lub części. Taka sytuacja wymaga generowania sąsiednich ortofotografii w ten sposób aby posiadały one wspólny obszar pokrycia. Ten obszar jest wykorzystywany do łączenia geometrycznego i uzgodnienia radiometrycznego styków,
W programie Phodis-Op mozaikowanie jest realizowane sekwencyjnie w szeregach. Program wyświetla dwa sąsiadujące ortofotografie definiując w jakim obszarze można wyznaczyć granicę połączenia - cięcia dla tych obrazów. Samą granicę ustala operator poprzez zdefiniowanie polilinii ograniczając do minimum przecinanie obiektów liniowych. Wzdłuż określonej w ten sposób granicy zostanie dokonane połączenie dwóch obrazów w jeden. Jednocześnie następuje wyrównanie radiometryczne. Ten proces jest wykonywany w pasie ok. 100 pikseli od wyznaczonej granicy cięcia. Następuje korygowanie wartości radiometrycznych pikseli w tym pasie w ten sposób, że wartość tonalna wynikowa jest średnią wartością tonalną obrazów pierwotnych wagowaną proporcjonalnie do odległości od krawędzi do obrazu pierwotnego.
Ten sposób mozaikowania jest zadawalający przy poprawnie zeskanowanych zdjęciach charakteryzujących się zbliżoną charakterystyką spektralną. Przy znacznych różnicach tonalnych taki proces nie daje zadawalających rezultatów i na wynikowym ortoobrazie wyraźnie wyróżniają się obrazy źródłowe.
W takich przypadkach trzeba stosować specjalne oprogramowanie wykonujące korekcję w zespole zdjęć cyfrowych. Dla tego celu jest oferowane specjalne oprogramowanie np.: Ortho-Yista firmy Zeiss pozwalające na usuwanie powyższych mankamentów oraz dodatkowo poprawiających kontrasty wynikowej ortofotomapy z wielu zdjęć jednocześnie w sposób automatyczny. MOZAIKOWANIE OBRAZÓW:mozaikowanie ortofotomapy:jeżeli mamy arkusz ortofotomapy to aby wypelnic ten obszar fotomapy wystarczy jedno zdjecie, ale tak jest nie zawsze.Problem mozaikowania-skladania jednej ortofotomapy z kilku ortoobrazow. W przypadku 2 zdjec wykonywanych w celu utworzenia ortofotomapy. Generujemy 2 ortofotomapy i bierzemy pod uwage bledy które będą ujawniać się na styku * bledy geometryczne- granica składania nie może przebiegac w poprzek drogi!, linia zakladania wzdluz rowow, drog. *bl radiometryczne. Mozaikowanie można wykonywac recznie ale to czasem nie wystarczy. Istnieja algorytmy automatyczne wpasowania. Jak sprawdzic aby radiometryczne obrazy pasowaly-trzeba przetransformowac radiometrycznie obrazy, może być to przeksztalcenie afiniczne tylko w przestrzeni RGB.Jak przetransformowac->Ponieważ mamy pokrycie pmiedzy zdjeciami dlatego możemy wykonac transformacje bo mamy punkty dostosowania, które wybieramy z obszaru podwojnego pokrycia.Tła wspólnego obzaru ustala histogram. W wyniku transformacji histogram 1 musi przybrac postac histogramu2:)
23. OBRAZY SATELITARNE
System obrazowania oparty jest na zasadzie skanera elektrooptycznego. W płaszczyźnie ogniskowej układu optycznego umieszczona jest linijka detektorów (CCD) dającą linie obrazu w kierunku poprzecznym do kierunku orbity, obraz w kierunku orbity tworzony jest w sposób ciągły, w wyniku ruchu satelity. O zdolności rozdzielczej decyduje wysokość orbity, ogniskowa układu optycznego i wymiary samych pikseli. Zdolność ta charakteryzow. jest przez terenowy wymiar piksela. W płaszczyźnie ogniskowej znajduje się zwykle linijka detektorów rejestrująca w zakresie widzialnym - tryb panchromatyczny, oraz linijki rejestrujące w wąskich podzakresach spektrum, zwykle niebieskim, zielonym, czerwonym i podczerwonym - tryb wielospektralny. Regułą jest, że rozdzielczość w trybie wielospektralnym jest gorsza - piksel jest zwykle 4 razy większy. Wysokorozdzielcze systemy maja dużą rozdzielczość radiometryczną, tj. zdolność rozróżniania wielkości odbicia obiektów naziemnych. Układ optyczny może być wychylany w dużym przedziale kątowym w przód i wstecz oraz na boki. ”Surowe” obrazy, zwykle po wstępnej korekcji geom. i radiometr., uzupełnione o model geometr. kamery i parametry orbity nadają się do dalszego opracowania, np. tworzenia ortofotomap czy automatycznej klasyfikacji. W przypadku obrazów stereoskopowych możliwe jest generowanie NMT lub stereodigitalizacja (przestrzenny pomiar, np. dla tworzenia mapy wektorowej).Obrazy ortorektyfikowane, przetworzone do wybranej projekcji kartograficznej na wybraną elipsoidę. Pojedyncze obszary mogą być mozaikowane w ciągły obraz większego obszaru. Zdjęcia sat. stosuje się w meteorologii, określania stopnia zanieczyszcz. atmosfery, do obserwacji chmur, w geologii - do badania ukształt. dna mórz i oceanów, do poszukiwań złóż surowców min., w hydrologii - do badania wielkości falowania oceanów, prądów morskich, zasobów wód na lądach i stanu ich czystości, w rolnictwie - do badania gleb, ich uwilgotnienia, rozwoju roślin, w leśnictwie - szybkie wykrywanie pożarów, plag szkodników i innych chorób lasów, w kartografii - do wykonania map użytkowania ziemi, kartowanie obszarów niedostępnych.
![]()
![]()
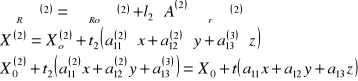
Wyszukiwarka