LABORATORIUM ELEKTROTECHNIKI

Sprawozdanie z ćw nr 1 : Pomiary impedancji metodą techniczną

1. Cel ćwiczenia.

Celem ćwiczenia jest poznanie metody technicznej wyznaczania rezystancji i reaktancji. W trakcie pomiarów uwzględnia się wpływ mierników na wyniki i oblicza się poprawkę oraz wyznacza niepewność pomiaru.

2. Wiadomości teoretyczne.

• Rezystancja czyli opór elektryczny(czynny) który występuje w obwodach prądu zmiennego jak i stałego. Zjawisko to jest związane z wydzielaniem się ciepła przy przepływie prądu. Wydzielana energia cieplna jest rozpraszana, powstaje ona kosztem energii elektrycznej pobieranej ze źródła zasilającego obwód elektryczny. Rezystancja jaka występuje na przewodzie wyraża się wzorem:

[Ω]

gdzie:

l - długości

s - przekrój

q - opór właściwy

Ilość wydzielanej energii cieplnej Q jest wyrażona wzorem:

Q=RI²t

• Reaktancja czyli opór bierny który stawia obwodowi cewka czyli reaktancja indukcyjna lub przez kondensator czyli reaktancja pojemnościowa. Reaktancja jest właściwością cewki lub kondensatora zależną od częstotliwości:

X_L=
=ωL, X_C=

Reaktancji pojemnościowej przypisuje się wartości ujemne, związane jest to z przesunięciem w fazie prądu względem napięcia w przeciwną stronę niż w przypadku reaktancji indukcyjnej.

• Impedancja (
  ) jest wielkością charakteryzującą elementy elektryczne w obwodach prądu zmiennego. Definiujemy ją jako iloraz napięcia i prądu (w tym samym elemencie), przy czym wielkości te wyrażone są wektorowo

Wektor może być wyrażony w postaci wykładniczej:

Wektor
możemy rozłożyć na składowe czynną i bierną (urojoną). Graficzne przedstawienie impedancji i jej składowych jest nazywane trójkątem impedancji.

Impedancja na rezystancji:

=R

Impedancja na rzeczywistej cewce:

Impedancja na rzeczywistym kondensatorze:

Impedancja obwodu RLC:

Wartość modułową impedancji zapisujemy jako:

• Metoda techniczna jest to metoda pośrednia jest to metoda pomiarowo-obliczeniowa, w której nieznaną impedancję Z wyznaczamy pośrednio z pomiaru prądu i napięcia. W tej metodzie wykorzystujemy trzy podstawowe mierniki takie jak woltomierz, amperomierz i w niektórych układach watomierz. W metodzie tej rozróżniamy dwa schematy podłączenia mierników w celu zmniejszenia błędu pomiarowego:

Rys. 1 Schematy metody technicznej pomiaru rezystancji

a) układ do pomiaru rezystancji dużych

b) układ do pomiaru rezystancji małych

UKŁAD DO POMIARU REZYSTANCJI DUŻYCH, WIĘKSZYCH OD 1.

W układzie jak na rys a). amperomierz mierzy prąd przepływający przez rezystancję R_X, czyli: I_A=I_X, natomiast woltomierz mierzy sumę spadków napięć na rezystancji R_X oraz na amperomierzu, czyli

gdzie: R_A - rezystancja wewnętrzna amperomierza.

Rezystancja obliczona na podstawie wskazań przyrządów wyraża się wzorem

Zatem błąd metody pomiaru wynosi

Rezystancja wewnętrzna amperomierza R_A jest niewielka zazwyczaj rzędu ułamka oma. Błąd metody będzie zatem tym mniejszy, im większa będzie rezystancja mierzona R_X. Gdy R_X>100R_A, to błąd wynikający z pominięcia poprawki nie przekroczy 1%. Układ z rys.a). należy zatem stosować do pomiaru rezystancji dużych.

UKŁAD DO POMIARU REZYSTANCJI MAŁYCH, MNIEJSZYCH OD 1.

W układzie jak na rys b). woltomierz wskazuje spadek napięcia na rezystancji mierzonej, czyli U_V=U_X, natomiast amperomierz mierzy sumę prądów przepływających przez rezystancję badaną i woltomierz:

przy czym prąd woltomierza:

gdzie: R_V - rezystancja wewnętrzna woltomierza.

Dla tego układu można napisać:

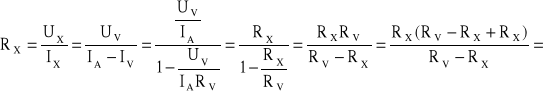
, gdzie

Bezwzględny błąd metody pomiaru wyniesie:

Rezystancja woltomierza jest na ogół bardzo duża. Błąd metody jest tym mniejszy, im rezystancja mierzona R_X jest mniejsza od rezystancji woltomierza R_V.

Gdy R_X<100R_V, to błąd wynikający z pominięcia poprawki, nie przekroczy 1%. Układ z rys. b). należy stosować do pomiaru rezystancji małych.

W praktyce układ z rys b). stosuje się do pomiaru rezystancji mniejszych od 1, natomiast układ z rys. a, do pomiaru rezystancji większych od 1. Poprawki wyznacza się przy pomiarach dokładnych i wówczas konieczna jest znajomość rezystancji wewnętrznych zastosowanych przyrządów. W celu oszacowania błędu pomiaru rezystancji, oprócz błędu metody należy uwzględnić błędy systematyczne przyrządów stosowanych w układzie.

Zaletą metody technicznej jest możliwość pomiaru rezystancji urządzeń (elementów) znajdujących się w stanie pracy.

Metoda techniczna pomiaru indukcyjności bądź pojemności prądem przemiennym jest szczególnie przydatna wówczas, kiedy mamy do czynienia z elementami nieliniowymi, np. cewka z rdzeniem ferromagnetycznym. Impedancja takich elementów zależy od wartości przepływającego przez nie prądu, co praktycznie uniemożliwia korzystanie z metod mostkowych.

Podobnie, jak w przypadku pomiarów rezystancji metodą techniczną prądem stałym, do pomiaru impedancji prądem przemiennym można stosować dwa układy pomiarowe (Rys.2)

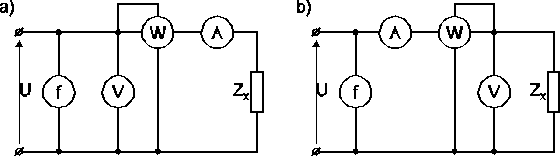
Rys.2. Schematy metody technicznej pomiaru impedancji

a) układ do pomiaru impedancji dużych

b) układ do pomiaru impedancji małych

• Metoda mostkowa przy użyciu technicznego mostka Wheatstone'a

Schemat mostka Wheatstone'a przedstawiony jest na rys 3.

Zawiera on cztery ramiona, w które włączone są trzy znane oporniki regulowane R₂, R₃, R₄, oraz rezystancja mierzona R_x.

Rys.3. Mostek Wheatstone'a

Pomiar rezystancji R_X polega na doprowadzeniu mostka do stanu równowagi, w którym przez galwanometr G nie płynie prąd (I_q=0). Oznacza to, że potencjały punktów C i D są jednakowe, czyli U_CD=0. W stanie równowagi obowiązują zależności:

I_X=I₂ I₃=I₄ (1)

oraz

I_XR_X=I₃R₃ R₂I₂=I₄R₄ (2)

Dzieląc stronami wyrażenia (1) oraz uwzględniając (2) otrzymamy:

czyli

W mostkach technicznych rezystancje R₃ i R₄ zastąpione są oporowym drutem ślizgowym, po którym przesuwa się ruchomy styk. Styk ten zaopatrzony jest w tarczę z podziałką pozwalającą odczytać wartość stosunku . Rezystor R₂ wykonany jest jako dekadowy, umożliwiający nastawienie następujących wartości: 0,01; 0,1; 1; 0,01; 10; 100; 1000.

Wszystkie elementy układu mostkowego, łącznie ze źródłami zasilającymi w mostkach technicznych umieszczone są we wspólnej obudowie miernika. Możliwe jest również zasilanie mostka ze źródła zewnętrznego.

Zakres pomiarowy mostka Wheatstone'a zawiera się najczęściej w granicach od 1 do 10⁴. Dolna granica wynika z wpływu dodatkowej rezystancji przewodów łączeniowych oraz rezystancji miejsc styku przewodów z badanym rezystorem na rezystancję mierzoną R_X. Górna granica zakresu pomiarowego jest uzależniona od czułości zastosowanego wskaźnika równowagi mostka (galwanometru), wartości napięcia źródła zasilania oraz rezystancji R₂, R₃ i R₄.

Rys.4 Mostek techniczny Wheatstone'a z drutem ślizgowym - AB

Z problemami tymi wiąże się także pojęcie czułości względnej mostka. Można stwierdzić, że czułość względna mostka (miara jego dokładności) jest największa, gdy:

- napięcie zasilające mostek będzie miało wartość maksymalną,

- czułość prądowa galwanometru będzie jak największa,

- rezystancja w gałęzi drugiej będzie równa rezystancji mierzonej, a rezystancja w gałęzi trzeciej będzie zawarta w przedziale R₃=(0,01...0,1)R_X.

Dokładność pomiaru w mostkach technicznych o drucie ślizgowym jest rzędu kilku procent. Znacznie większą dokładność oraz lepszy zakres pomiarowy zapewnia układ dekadowy mostka Wheatstone'a. W układzie tym rezystory R₂, R₃, R₄ wykonane są jako oporniki dekadowe, czyli oporniki o dużej dokładności i wartościach różniących się dziesięciokrotnie np. 1, 10, 100, 1000, 10000. Napięcia zasilania takiego mostka wynosi kilkadziesiąt woltów.

3. Schemat pomiarowy:

Rys.5. Schemat obwodu badanego

4. Wykaz przyrządów:

1. Autotransformator

2. Amperomierz Vc N_o 99163546

3. Woltomierz elektromagnetyczny o klasie 0,5 Nr INW. N. 7-2335

4. Watomierz ferrodynamiczny o klasie 0,5 Nr INW. N. 7-4834

5. Przebieg ćwiczenia:

Ćwiczenie rozpoczynamy od zapoznania się z instrukcją, zastanowieniu się jakich przyrządów będziemy potrzebowali i co będziemy mierzyli. Po wykonaniu tych czynności przystępujemy do podłączenia układu pomiarowego zgodnie ze schematem i ustawieniu mierników na odpowiednie zakresy. Pierwszy pomiar dokonujemy wstawiając w miejsce Z_x element nieliniowy(żarówkę) i ściągamy jego charakterystykę. Drugi pomiar dokonujemy wstawiając dławik w ten sam układ pomiarowy. Trzeci pomiar dokonujemy na kondensatorze postępując dokładnie jak przy pomiarze pierwszym. Z otrzymanych wyników obliczamy potrzebne nam parametry które były uwzględnione w instrukcji.

6. Tabele pomiarowe, charakterystyki:

We wszystkich obliczeniach, w których występuje częstotliwość, zakładamy, że jest ona równa 50Hz.

• Wyznaczanie charakterystyki obiektu nieliniowego

Badanym opornikiem jest żarówka głównego szeregu o napięciu znamionowym 230V. Pomiary należy przeprowadzić w zakresie od 0 do 230 V, zmieniając napięcie za pomocą autotransformatora. Żarówkę włączamy jako odbiornik Z_x (zgodnie z schematem powyższym)

Nr		1	2	3	4	5	6	7	8	9	10	11	12
U	V	22	44	60	80	100	120	136	156	176	196	216	224
I	A	0,126	0,155	0,180	0,204	0,226	0,247	0,266	0,285	0,303	0,320	0,337	0,344
P	W	2,75	6,5	10,5	16	24,5	29	36	49	52	61,5	71	76

• Pomiar metodą techniczną impedancji cewki i jej składowych oraz indukcyjności

Pomiar wykonuje się w układzie według rysunku, włączając badany dławik jako odbiornik Z_x

Z_L=U/I cosφ=P/UI
X_L=Zsinφ R_L=Zcosφ L=X_L/2πf

Nr		1	2	3	4	5	6	7	8
U	V	22	44	60	80	96	118	134	156
I	A	0,102	0,186	0,276	0,376	0,469	0,607	0,754	0,971
P	W	1	3	5,5	10	14	20	28	38
ZL	Ω	215,7	236,6	217,4	212,8	204,7	194,4	177,7	160,7
cosφ		0,44	0,24	0,33	0,33	0,31	0,279	0,277	0,237
sinφ		0,898	0,97	0,944	0,944	0,95	0,96	0,96	0,97
XL	Ω	193,6	229,5	256,2	225,4	194,47	186,6	170,59	165,7
RL	Ω	94,9	56,78	71,74	70,22	63,457	54,24	49,22	38,08
L	H	0,616	0,73	0,82	0,717	0,62	0,594	0,54	0,527

• Pomiar metodą techniczną impedancji oraz pojemności kondensatora

Pomiar wykonuje się w układzie, według załączonego rysunku, włączając badany kondensator jako odbiornik Z_x

Z_c=U/I X_c=Z_c C= 1/2πfX_c

Nr		1	2	3	4	5	6	7	8	9	10	11	12
U	V	22	44	60	80	100	120	138	156	176	196	216	224
I	A	0,013	0,027	0,039	0,052	0,064	0,076	0,089	0,103	0,116	0,130	0,141	0,150
P	W	0	0	0	0	0	0	0	0	0	0	0	0
Zc	Ω	1692	1629	1538	1538	1563	1579	1551	1515	1517	1508	1532	1493
Xc	Ω	1692	1629	1538	1538	1563	1579	1551	1515	1517	1508	1532	1493
C	μF	1,88	1,95	2,07	2,07	2,04	2,02	2,05	2,10	2,098	2,11	2,08	2,13

7. Przykłady obliczeń:

P_w=38W

P_p=

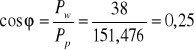
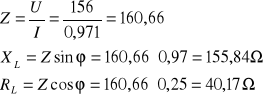
9. Dyskusja błędów pomiarowych:

Błędy pomiarowe jakie wyszły nam w ćwiczeniu wynikają z doboru mierników jak i nie precyzyjnego odczytu z mierników. W naszym trzecim pomiarze przy badaniu kondensatora wyszło nam, że badany kondensator jest idealny co jest nie prawdą stało się tak ponieważ moc czynna kondensatora jest niewielka a my mieliśmy watomierz o dużym zakresie.

10. Uwagi i wnioski:

Moc czynna dławika jest duża, ale wynika to z budowy dławika, nie mieliśmy żadnych danych tego elementu. A pomiar został wykonany tylko do napięcia 160V ponieważ dalej przekroczylibyśmy zakres cewki prądowej watomierza. Metoda, którą poznaliśmy, pozwala na wyznaczenie w prosty sposób parametrów danych elementów w układzie.

Sprawozdanie wykonali: Różalski Dariusz, Nowak Marzena, Polny Piotr, Przybyłek Aleksander, Babis Karol

---