LABORATORIUM FIZYKI I |
Ćwiczenie nr: Data:
25 13.11.08r. |
|||
Wydział: WIP |
Grupa: WI - 3.3 |
Zespół: 4 |
Punktacja |
Przygotowanie |
Nazwisko i imię: Olszówka Jakub |
|
|
||
Temat ćwiczenia:
Zjawisko interferencji światła, pierścienie Newtona, interferometr Michelsona. |
|
Sprawozdanie |
||
Prowadzący:
|
|
Suma punktów: |
||
1.Wstęp.
Celem ćwiczenia było zaobserwowanie i zbadanie zjawiska interferencji światła. Sprawdzenie zależności promieni okręgów interferencyjnych od długości fali oraz obliczenie za pomocą tych zależności nieznanej długości fali .
2. Schemat pomiarowy.
Bieg promieni przy powstawaniu pierścieni Newtona:
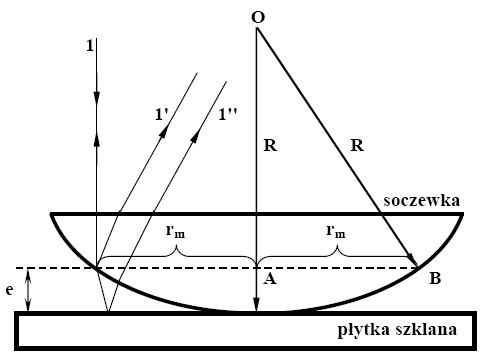
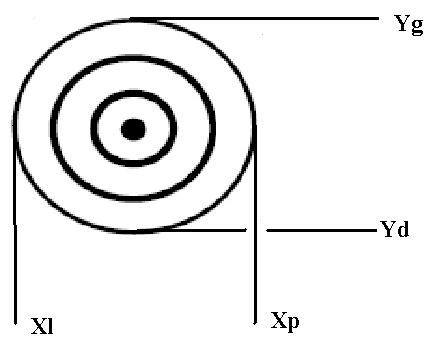
Obserwowany obraz:
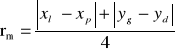
3. Wykonanie ćwiczenia.
Pierścienie Newtona
1.Ustawienie urządzenia, przygotowanie świateł (jedno o =589,3 nm oraz dwa źródła światła o nieznanej długości fali.)
2. Pomiar wymiarów xl, xp, yd, oraz yg potrzebnych do obliczenia promieni pierścieni rm według podanego wzoru dla wszystkich rodzajów światła.
3.Wykonanie niezbędnych obliczeń oraz wyznaczenie błędów pomiaru.
Interferometr Michelsona:
1.Ustawienie urządzenia. Wyzerowanie licznika, ustawienie śruby mikrometrycznej w odpowiedniej pozycji
2. Pomiar wymiarów impulsów podczas przesuwania zwierciadła śrubą mikrometryczną.
3.Wykonanie niezbędnych obliczeń oraz wyznaczenie błędów pomiaru.
4. Wyniki ćwiczenia.
Pierścienie Newtona:
1) Wyniki dla lampy sodowej o =589,3 nm.
m |
xp |
xl |
yg |
yd |
rm =(|xp-xl|+|xg-xd|)/4 |
Lampa sodowa - filtr biały |
[mm] |
||||
1 |
19,91 |
17,59 |
7,00 |
9,30 |
1,1550 |
2 |
20,32 |
17,15 |
6,57 |
9,74 |
1,5850 |
3 |
20,68 |
16,82 |
6,26 |
10,07 |
1,9175 |
4 |
20,99 |
16,55 |
5,97 |
10,37 |
2,2100 |
5 |
21,23 |
16,31 |
5,71 |
10,63 |
2,4600 |
6 |
21,45 |
16,28 |
5,48 |
10,85 |
2,6350 |
7 |
21,67 |
15,86 |
5,27 |
11,05 |
2,8975 |
8 |
21,86 |
15,65 |
5,07 |
11,27 |
3,1025 |
9 |
22,03 |
15,45 |
4,90 |
11,45 |
3,2825 |
10 |
22,15 |
15,30 |
4,73 |
11,64 |
3,4400 |
Promień pierścienia m:
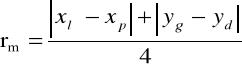
Grubość promienia m=1 wynosi : 0,25 [mm]
Grubość promienia m=10 wynosi : 0,02 [mm]
Stały skok pomiędzy promieniami wyniósł 0,256 [mm]
Błąd systematyczny :
![]()
Wykres zależności ![]()
w funkcji![]()
dla światła o znanej długości fali równej 589,3 nm.
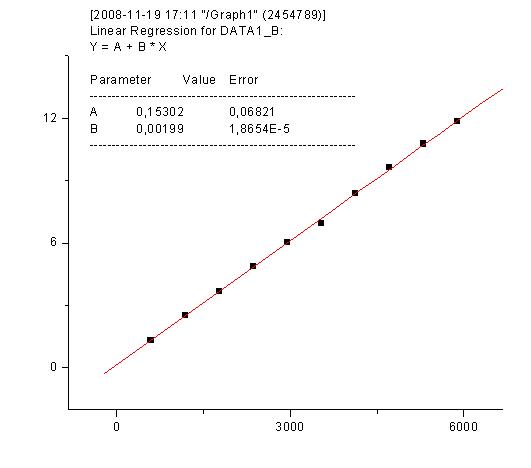
Z pomocą metody najmniejszej sumy kwadratów:
![]()
oraz 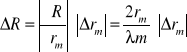
m |
Promień pierścienia |
Grubość pierścienia |
|
|
|
[mm] |
[mm] |
[mm] |
[mm] |
1 |
1,1550 |
0,25 |
2263,75 |
196 |
2 |
1,5850 |
0,224 |
2131,53 |
134,48 |
3 |
1,9175 |
0,199 |
2079,76 |
108,46 |
4 |
2,2100 |
0,173 |
2071,99 |
93,76 |
5 |
2,4600 |
0,148 |
2053,83 |
83,49 |
6 |
2,6350 |
0,72 |
1963,69 |
74,52 |
7 |
2,8975 |
0,096 |
2035,22 |
70,24 |
8 |
3,1025 |
0,07 |
2041,72 |
65,81 |
9 |
3,2825 |
0,045 |
2031,56 |
61,89 |
10 |
3,4400 |
0,02 |
2008,08 |
58,37 |
Tak więc uśredniona wartość R i ![]()
R z dziesięciu pomiarów :
R![]()
![]()
R = 21* 102 ![]()
95 [mm]
Wyniki pomiarów i wykresy zależności ![]()
od R*m dla źródeł światła o nieznanej długości fali:
Światło białe - filtr zielony
m xp xl yg yd |
[mm] |
||||
1 |
19,53 |
17,51 |
7,22 |
9,23 |
1,0075 |
2 |
19,96 |
17,10 |
6,78 |
9,62 |
1,4250 |
3 |
20,25 |
16,77 |
6,43 |
9,96 |
1,7525 |
4 |
20,54 |
16,50 |
6,16 |
10,20 |
2,0200 |
5 |
20,76 |
16,26 |
5,93 |
10,44 |
2,2525 |
6 |
20,98 |
16,08 |
5,72 |
10,67 |
2,4625 |
7 |
21,17 |
15,87 |
5,53 |
10,85 |
2,6550 |
8 |
21,38 |
15,68 |
5,34 |
11,05 |
2,8525 |
9 |
21,55 |
15,51 |
5,17 |
11,22 |
3,0225 |
10 |
21,64 |
15,35 |
5,06 |
11,36 |
3,1475 |
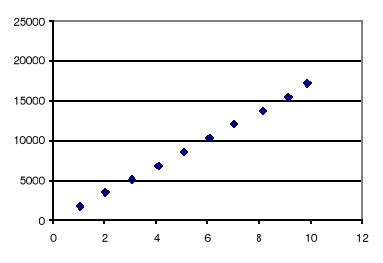
Wykres:
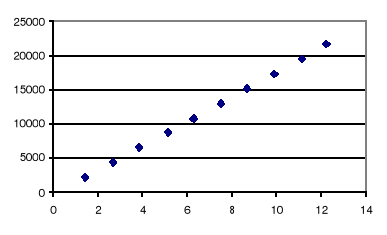
![]()
Obliczenie długości fali wraz z odchyleniem standardowym :
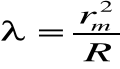
![]()
= 619 ![]()
29 [nm]
Oraz światło drugie:
Światło białe - filtr czerwony
m xp xl yg yd |
[mm] |
||||
1 |
19,67 |
17,27 |
6,97 |
9,39 |
1,2050 |
2 |
20,09 |
16,83 |
6,55 |
9,80 |
1,6275 |
3 |
20,43 |
16,50 |
6,21 |
10,16 |
1,9700 |
4 |
20,73 |
16,21 |
5,92 |
10,46 |
2,2650 |
5 |
21,00 |
15,98 |
5,68 |
10,68 |
2,5050 |
6 |
21,22 |
15,71 |
5,45 |
10,91 |
2,7425 |
7 |
21,42 |
15,53 |
5,26 |
11,13 |
2,9400 |
8 |
21,62 |
15,32 |
5,05 |
11,34 |
3,1475 |
9 |
21,82 |
15,13 |
4,85 |
11,52 |
3,3400 |
10 |
21,96 |
14,94 |
4,70 |
11,68 |
3,5000 |
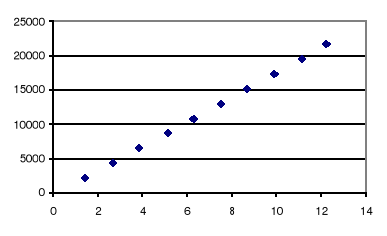
Wykres:
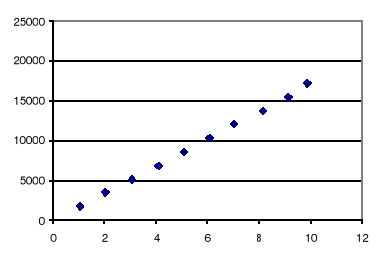
![]()
Obliczenie długości fali wraz z odchyleniem standardowym:
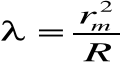
![]()
= 490 ![]()
14 [nm]
Interferometr Michelsona:
Przesuw śruby mikrometrycznej |
Wynik |
12,0 - 12,5 |
201 |
12,5 - 13,0 |
215 |
13,0 - 13,5 |
319 |
13,5 - 14,0 |
400 |
14,0 - 13,5 |
319 |
13,5 - 13,0 |
324 |
13,0 - 12,5 |
214 |
12,5 - 12,0 |
233 |
12,0 - 12,5 |
174 |
12,5 - 13,0 |
354 |
13,0 - 13,5 |
138 |
13,5 - 14,0 |
370 |
14,0 - 13,5 |
255 |
13,5 - 13,0 |
314 |
13,0 - 12,5 |
279 |
12,5 - 12,0 |
235 |
Wyliczona wartość średnia impulsów wyniosła: 271,15
Odchylenie standardowe sigma : 72,47
Ustalony poziom ufności wynosi 68%
Wynik to 272![]()
73
Dane spełniające pierwszy test to:
201, 215, 319, 319, 324, 214, 233, 255, 314, 279, 235
Drugi test:
Wyliczona wartość średnia impulsów wyniosła: 263,36
Odchylenie standardowe sigma : 45,65
Ustalony poziom ufności wynosi 68%
Ostateczny wynik to 264![]()
46 impulsów.
5. Wnioski z ćwiczenia.
Z obserwacji podczas ćwiczeń oraz wyników obliczeń stwierdzamy, że za pomocą dostępnych urządzeń trudno jest obliczyć dokładne wartości promieni okręgów interferencyjnych, głównie przez niedokładność ludzkiego oka.
Wykres zależności r2 w funkcji λm dla światła lampy sodowej układa się liniowo, co potwierdza, że wartość R - krzywizna soczewki jest wartością stałą, (niedokładności położenia punktów są wynikiem błędów pomiaru), podobnie wykresy nieznanych wartości lambda dla pozostałych źródeł światła, są one liniowe co oznacza stałą wartość długości światła, i prawidłowe wykonanie wykresów.
Sporych trudności nastręczało wykonanie ćwiczenia za pomocą interferometru, spowodowane to było dużą rozpiętością wyników przez nieuważne bądź niedokładne ustawianie śruby mikrometrycznej. Należało wykonać odpowiednie przybliżenia i rachunek błędów aby obliczyć przybliżone wartości impulsów zanotowane na urządzeniu. Długości fal zgadzają się z widmem światła białego ( fal elektromagnetycznych), dłuższa fala wpada w kolor zielony, a krótsza, w czerwony.
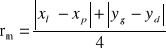
R- promień krzywizny soczewki
rm- promień pierścienia Newtona rzędu `m'
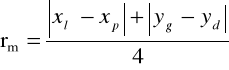
R*m
![]()
R*m
![]()
![]()
![]()
Wyszukiwarka