POLITECHNIKA ŚLĄSKA
WYDZIAŁ INŻYNIERII MATERIAŁOWEJ I METALURGII
Nazwisko i imię NATALIA ORLIKOWSKA, KAMIL MARCINEK
Grupa ZIP22
Sekcja IV
SPRAWOZDANIE
z fizyki - laboratorium
POMIAR CZASU ZDERZEŃ KUL I WYZNACZANIE PARAMETRÓW DEFORMACJI.
Uwagi prowadzącego:
OPIS ĆWICZENIA
Pomiary odległości kul gdy kule zwisają swobodnie - Wykonanie pomiaru odległości kul od podstawy podczas gdy kule te zwisają swobodnie .
Pomiary napięcia na kondensatorze przed zderzeniem (Uo, V), oraz po zderzeniu (U, V) -
Uruchomienie zasilacza i ustawienie napięcia na 30 V.
Odchylenie kulek tak aby dotknęły elektromagnesów i pięciokrotnie zmierzenie ich odległości od podstawy.
Następnie naładowanie kondensatora, poprzez zamknięcie na kilka sekund wyłącznika W1 i zanotowanie napięcia Uo, a następnie co 10s notować wartości napięcia U, jakie wskazuje woltomierz.
Naładowanie ponownie kondensatora i naciśnięcie wyłącznika W2, zwalniając kule. Po zderzeniu, nie dopuszczenie do ponownego zderzenia kul. Zanotowanie napięcia, na chwilę po zderzeniu, pomiary te wykonano pięciokrotnie, dla dziesięciu wartości R (od 1 Ohm do 10 Ohm, co 1 Ohm).
Wartości średnie i odchylenia standardowe dla wykonanych pomiarów.
Wartości średnie obliczono na podstawie wzoru:
Odchylenia standardowe na podstawie wzoru:
Odległość kul od podstawy [mm] |
Średnia [mm] |
Odchy-lenie standardo-we σ [mm] |
|||||
Gdy zwisają swobodnie (H1) |
105 |
106 |
106 |
106 |
105 |
105,6 |
0,24495 |
Gdy są przyciągane przez elektromagnesy (H2) |
118 |
119 |
118 |
118 |
119 |
118,4 |
0,24495 |
H=H2 - H1 |
13 |
13 |
12 |
12 |
14 |
12,8 |
0,14 |
|
Pomiary [V] |
|
||||||
|
Opór [Ω] |
1 |
2 |
3 |
4 |
5 |
Średnia [V] |
Odchylenie standardo-we σ [V] |
Kondensator |
1 |
29,6 |
29,6 |
29,6 |
29,6 |
29,6 |
29,6 |
0 |
Zderzenie |
|
0,02 |
0,02 |
0,02 |
0,02 |
0,02 |
0,02 |
0 |
Kondensator |
2 |
29,6 |
29,6 |
29,6 |
29,6 |
29,6 |
29,6 |
0 |
Zderzenie |
|
0,05 |
0,07 |
0,05 |
0,06 |
0,05 |
0,056 |
0,004 |
Kondensator |
3 |
29,6 |
29,6 |
29,6 |
29,6 |
29,6 |
29,6 |
0 |
Zderzenie |
|
2,2 |
2,1 |
2,0 |
2,1 |
2,1 |
2,8 |
0,037417 |
Kondensator |
4 |
29,6 |
29,6 |
29,6 |
29,6 |
29,6 |
29,6 |
0 |
Zderzenie |
|
4,1 |
4,0 |
4,0 |
4,1 |
4,0 |
4,04 |
0,024495 |
Kondensator |
5 |
29,6 |
29,6 |
29,6 |
29,6 |
29,6 |
29,6 |
0 |
Zderzenie |
|
5,6 |
5,4 |
5,7 |
5,5 |
5,6 |
5,56 |
0,05099 |
Kondensator |
6 |
29,6 |
29,6 |
29,6 |
29,6 |
29,6 |
29,6 |
0 |
Zderzenie |
|
7,5 |
6,6 |
7,1 |
6,6 |
6,6 |
6,88 |
0,182757 |
Kondensator |
7 |
29,6 |
29,6 |
29,6 |
29,6 |
29,6 |
29,6 |
0 |
Zderzenie |
|
8,3 |
8,4 |
8,3 |
7,6 |
8,6 |
8,24 |
0,169115 |
Kondensator |
8 |
29,6 |
29,6 |
29,6 |
29,6 |
29,6 |
29,6 |
0 |
Zderzenie |
|
9,7 |
9,4 |
9,2 |
9,2 |
9,6 |
9,42 |
0,10198 |
Kondensator |
9 |
29,6 |
29,6 |
29,6 |
29,6 |
29,6 |
29,6 |
0 |
Zderzenie |
|
10,6 |
11,5 |
11,2 |
10,5 |
10,6 |
10,88 |
0,198494 |
Kondensator |
10 |
29,6 |
29,6 |
29,6 |
29,6 |
29,6 |
29,6 |
0 |
Zderzenie |
|
12,0 |
12,5 |
11,7 |
12,2 |
11,7 |
12,02 |
0,152971 |
Wykres zależności
od wartości oporu R dla uśrednionych wyników.
Oś X |
Oś Y |
Opór R [Ω] |
|
1 |
0,136990104 |
2 |
0,159485107 |
3 |
0,37659018 |
4 |
0,502126589 |
5 |
0,598023084 |
6 |
0,685327819 |
7 |
0,781998998 |
8 |
0,873408768 |
9 |
0,999152599 |
10 |
1,109628608 |
Parametry prostej aproksymującej,
Obliczono za pomocą poniższych wzorów

a = (0,109 ± 0,02) [1/]
b = (0,02 ± 0,13) [1]
Czas rozładowania kondensatora t.
Pojemność kondensatora C [μF] = 10, obliczono na podstawie wzorów:
oraz:
wiedząc, że:
otrzymujemy:
Oraz obliczenie t czasu rozładowania kondensatora, za pomocą wzoru
Wielkość ugięcia czaszy kuli h.
Dany jest wzór na wielkość ugięcia czaszy kuli 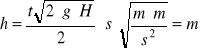
gdzie:
t = (0,09±0,02)*10- 3 [s] - czas rozładowania kondensatora g = 9,81 [m/s2] - przyspieszenie grawitacyjne H = H2 - H1 - różnica wysokości kul
Za pomocą tego wzoru, obliczono wielkość ugięcia czaszy kuli
Niepewność ugięcia h czaszy kuli podczas wgniecenia, obliczono za pomocą wzoru
WNIOSKI
- Wykres zależności 1/ln(Uo/U) = f(R), jest funkcją liniową. - Funkcja ta, posłużyła nam do wyznaczenia czasu t rozładowania kondensatora.
- Napięcie w kondensatorze, po zderzeniu zawsze kul stopniowo maleje. ( Jest to widoczne na wykresie, w którym w raz ze wzrastającym czasem, maleje wartość napięcia, na kondensatorze)
- Obliczenie średnich wartości i odchyleń standardowych, pozwoliło na zniwelowanie różnic pomiędzy poszczególnymi pomiarami, oraz na uzyskanie konkretnych wartości do dalszych obliczeń.
- Z wykresu zależności 1/ln(Uo/U) do oproru (Ohm), jesteśmy w stanie wywnioskować że wraz ze wzrostem oporu, wartość 1/ln(Uo/U), stopniowo wzrasta.
- Wielkość ugięcia czaszy kuli, zależy między innymi od czasu w jakim nastąpiło rozładowanie kondensatora.
- Obliczenie niepewności do każdych pomiarów, pozwoliło nam na określenie występujących błędów przy pomiarów.
Wyszukiwarka