![]()
ZAGADNIENIA DLA WGiOS
I-szy semestr
Oddziaływania fundamentalne w fizyce
-Oddzialywania fundamentalne są to oddziaływania, które możemy obserwować w przyrodzie dzielą się na :
- Grawitacja - będące zjawiskiem naturalnym polegającym na tym, że wszystkie obiekty posiadające masę oddziałują na siebie wzajemnie przyciągając się.
- Słabe - Jest odpowiedzialne za rozpad beta i związaną z nim radioaktywność oraz rozpad np mionu i cząstek dziwnych
- Elektromagnetyczne - stacjonarne pole elektromagnetyczne pozostaje związane ze swoim źródłem, zmiennne pole magnetyczne natomiast rozprzestrzenia się w postaci fali elektromagnetycznej.
- Silne - spośród cząstek elementarnych oddziałują tylko kwarki, antykwarki i gluony.
Przykłady wielkości fizycznych i ich podział
- Wielkości fizyczna to własność ciała lub zjawiska, którą można porównać ilościowo z taką samą własnościa innego ciała lub zjawiska np. długość, masa, natężenieDefinicje jednostek podstawowych w układzie SI
- Metr(m) - jest to długość drogi przebytej w próżni przez światło w czasie 1/299792458s
- Kilogram(kg) - jest to masa międzynarodowego wzoru jednostki masy przechowywanego w Międzynarodowym Biurze Miar w Serves pod Paryżem
- Sekunda(s) - jest to czas równy 9 192 631 770 okresom promieniowania odpowiadającego przejściu między dwoma nadsubtelnymi poziomami stanu podstawowego atomu cezu 133Cs
- Kelwin(K) - jest to 1/273,16 część temperatury termodynamicznej punkty potrójnego wody
- Mol(mol) - jest to liczność materii występująca, gdy liczba cząstek jest równa liczbie zawartych w masie 0,012 kg 12C
- Amper(A) - jest natężeniem prądu nie zmieniającego się, który płynąc w dwóch
Równoległych prostoliniowych przewodach nieskończenie długich o przekroju
Kołowym znikomo małym, umieszczonych w próżni w odległości 1 m wywołuje
Między tymi przewodami siłę równą ![]()
- Kandela(Cd) - jest to światłośc jaką ma w określonym kierunku źródło emitujące promieniowanie monochromatyczne o częstotliwości ![]()
Hz i którego natężenie w tym kierunku jest równe 1/681 W/Sr
- Steradian - jest kątem bryłowym o wierzchołku w środku kuli, wycinającym z jej
Powierzchni część równą powierzchni kwadratu o boku równym tej kuli
- Radiam - jest to płaski kąt zawarty między dwoma promieniami koła wycinającymi z jego okręgu łuk o długości równej promieniowi tego koła.
Wielkości wektorowe i skalarne
-Skalarne(posiadają tylko wartość) : masa, objętość, czas, droga, ładunek, praca, moc
- Wektorowe(posiadają : zwrot, kierunek, punkt przyłożenia) : prędkość, przyspieszenie, siła, moment siły, pędDodawanie i mnożenie wektorów
- Dodawanie wektorów możemy wykonać techniką graficzną, lub przez dodanie składowych tego wektora
- mnożenie wektorów
ILOCZYN SKALARNY
![]()
ILOCZYN WEKTOROWY
![]()
Kinematyka
-Opisuje ruch ciała
Definicja ruchu
- Przez ruch ciała rozumiemy zmiany jego położenia względem układu odniesienia
Rodzaje ruchu
- Postępowy - wszystkie punkty ciała poruszają się po takich samych torach
- Obrotowy - tory poszczególnych punktów ciała są okręgami współśrodkowymi
Prędkość średnia, chwilowa
- śr.
- ch.
Ruch prostoliniowy jednostajny
- v = const
S = V*t
Ruch prostoliniowy jednostajnie zmienny
- V = V(t)
Przyspieszenie średnie, chwilowe
- śr 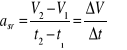
[m*s-2]
- ch. 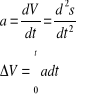
Ruch krzywoliniowy
Wektor wodzący i tor punktu
- V=V(t)
Równoważne równania skalarne
- X = x(t) y = y(t) z = z(t)
Prędkość i przyspieszenie w ruch krzywoliniowym
- 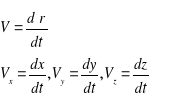
- przyspieszenie
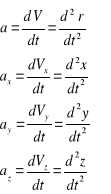
Rzut ukośny, rzut poziomy
- Rzut ukośny - ruch ciała, któremu nadano prędkość początkową V0
skierowaną pod kątem alfa do poziomu
W kierunku poziomym ruch jest jednostajny ze stałą prędkością:
Równanie poziome x = Vox*t
Pionowe : y = yoy * t - gt2/2 - w kierunku poziomym
Występuje stałe przyspieszenie ziemskie g skierowane w dół w kierunku ujemnym do osi y oraz prędkość początkowa Voy w kierunku dodatnim osi y.
Współrzędne dowolnego punktu na krzywej toru w dowolnym czasie t :
![]()
Równanie toru : ![]()
Zasięg rzutu : ![]()
Maksymalna wysokość : ![]()
To zasięg będzie największy; dla kątów alfa i 90 - alfa zasięg jest taki sam
Całkowity czas : ![]()
-Rzut poziomy : Prędkość ciała w każdym punkcie toru jest wypadkową
Prędkości stałej V0 w kierunku poziomym i prędkości pionowej
Vy = g*t Prędkość wypadkowa jest styczna do toru
Równanie toru : poziomo -x = V0*t
Pionowo : y = yo - gt2/2
Cały tor : ![]()
Zasięg poziomy rzutu : 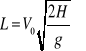
Ruch po okręgu
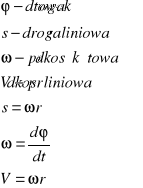
![]()
- prędkość liniowa, T - okres
![]()
[ ![]()
], ![]()
- prędkość kątowa
![]()
- częstość obrotów [![]()
] = 1 Hz ; ![]()
Przyspieszenie dośrodkowe: ![]()
- ma taki sam kierunek jak ![]()
, czyli ma kierunek zgodny z promieniem i zwrot do środka koła; ![]()
; z okresem - ![]()
![]()
[ ![]()
] - moment pędu
Cztery palce składamy w kierunku ruchu ciała, to wyciągnięty kciuk określa zwrot momentu pędu; Jest on prostopadły do okręgu.
Dynamika punktu materialnego
Pierwsza zasada dynamik
- Ciała nie poddane oddziaływaniu żadnych innych ciał albo pozostaje w spoczynku, albo porusza się ruchem jednostajnym prostoliniowym tzw. Zasada bezwładności
Druga zasada dynamiki
- siła działająca na ciało jest równa iloczynowi przyspieszenia i masy tego ciała
F = ma a = F/m
Trzecia zasada dynamiki
- Jeżeli ciało A działa na ciało B pewną siła FAB to ciało B działa na ciało A siła FBA równą co do wartości lecz przeciwnie skierowaną( zasada akcji i reakcji)
Pęd
- pędem ciała nazywamy iloczyn jego masy i prędkości
p = m * V
Przykłady sił występujących w mechanice
- siła sprężystości
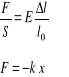
- siła tarcia
![]()
![]()
- współczynnik Tarcia N - nacisk ciała na podłoże
Dynamika ruchu punktu materialnego po okręgu
- ![]()
Okres ruchu - czas potrzebny na przebycie drogi kątowej 2pi
![]()
f - częstotliwość, liczba obiegów pkt, na jednostkę czasu
f = 1/T [1/s] = [Hz]
Przyspieszenie kątowe :
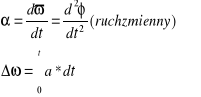
Przyspieszenie normalne i styczne - odpowiedzialne za zmianę wartości v(wektor), odpowiada za zmianę kier. V
Dynamika pkt. Mat po okręgu:
Fn=m*an=m*v2/r
Praca, moc, energia mechaniczna, energia kinetyczne
- Praca : dW = F*ds. = F*cos αds = Fds
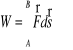
[J]=1N*m=1 kg* m2/s2
Moc:
: ![]()
![]()
[W] = 1J/s
Energia: Kinetyczna ( masa prędkość), Potencjalna ( masa położenie)
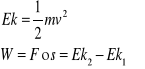
Energia potencjalna ciała w pkt. P wzg. Pkt 0 nazywamy pracę jaka wskazuje siła
Zachowawcza przy przesunięciu tego ciała od pkt. P do pkt. 0
Ep = mgh
Potencjalna energia sprężystości
![]()
Siły zachowawcze
Siłę nazywamy zachowawczą albo potencjalną jeżeli jej praca po dowolnym torze zamkniętym jest równa zeru
Praca w polu sił ciężkości
Praca siły zachowawczej nie zależy od kształtu drogi, a tylko od wyboru pkt. Początkowego i końcowego
Grawitacyjna energia potencjalna
Ep = m*g*h
Potencjalna energia sprężystości
Ep = ½ *k*x2
Dynamika układu punktów materialnych
Środek masy
Twierdzenie o ruchu środka masy
- środek masy punktów materialnych porusza się tak jak punkt materialny o masie równej całkowitej masie układu, na którym działa Fz równa wypadkowej sił zewnętrznych
Siły zewnętrzne i wewnętrzne
Dynamika bryły sztywnej, rodzaje ruchów bryły sztywnej
- Bryła sztywna - jest to ciało, które pod działaniem sił nie ulega odkształceniom tzn, odległość dwóch dowolnych punktów takiego ciała pozostają stała.
- Rodzaje ruchów :
- Ruch postępowy punktu materialnego jest to każdy ruch tego punktu opisywany przy użyciu wielkości charakterystycznych dla ruchu postępowego
- Ruch obrotowy to taki ruch, w którym wszystkie punkty bryły poruszają się po okręgach o środkach leżących na jednej prostej zwanej osią obrotu.
Moment siły
- Wielkość wywołująca ruch obrotowy nazywamy momentem siły. Moment siły F względem punktu O osi obrotu nazywamy iloczyn wektorowy wektora wodzącego i punktu przyłożenia siły F i tej siły
Moment bezwładności
- momentem bezwładności I bryły względem danej osi nazywamy sumę iloczynów mas mi poszczególnych punktow bryły i kwadratów Ri ich odległości od danej osi
Moment bezwładności niektórych brył:
Kula o r = R ![]()
Walec o r = R ![]()
Pręt o dł. l ![]()
Obręcz o r = R ![]()
Twierdzenie Steinera
- Momentem bezwładności I bryły względem dowolnej osi jest równy sumie momentu bezwładności I0 względem osi równoległej przechodzącej przez środek masy bryły oraz iloczynu masy tej były i kwadratu odległości „a” obu osi
Moment pędu
- Dla punktu materialnego : L = r x Mv
L = rmV=mr2 ![]()
L = mr2![]()
Dla bryly: L = ![]()
L = I ![]()
Moment pędu bryły równa się iloczynowi jej prędkości kątowej ![]()
i momentu bezwładności I
Momentem pędu L bryły względem czasu równa się momentowi M działającej na tę bryłę
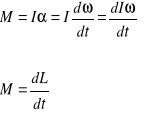
Pierwsza, druga, trzecia zasada dynamiki ruchu obrotowego
- I zasada ruchu obrotowego - Bryła sztywna nie poddana działaniu momentu siły pozostaje nieruchoma lub wykonuje ruch obrotowy jednostajny
- II zasada ruchu obrotowego - jeżeli wypadkowy moment sił działających na bryłę jest różny od zera to bryła porusza się zmiennym ruchem obrotowym z przyśpieszeniem kątowym wprost proporcjonalnym do wypadkowgo momentu sił, a odwrotnie proporcjonalnym do momentu bezwładności bryły względem wybranej osi
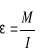
- III zasada ruchu obrotowego - Jeżeli bryła A działa na bryłę B momentem siły MAB to B działa na A momentem siły MBA równym co do wartości i przeciwnie skierowanym
Energia kinetyczna ruchu obrotowego
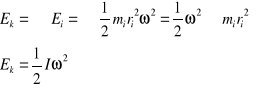
- Energia kinetyczna ruchu obrotowego równa się połowie iloczynu momentu bezwładności i kwadratu prędkości kątowej:
Toczenie się bryły
Zasady zachowania w mechanice
Zasada zachowania energii mechanicznej
- Układ odosobniony to taki układ, na który nie działają siły zewnętrzne. Jeżeli siły te są zachowawcze to taki układ będziemy nazywać układem zachowawczym.
Zasada zachowania pędu
- Jeżeli wypadkowa sił zewnętrznych działających na układ jest równa zeru to pęd całkowity tego układu jest stały.
Zasada zachowania momentu pędu - krętu
- Jeżeli moment wypadkowy sił zewnętrznych działających na układ równy jest zeru, to kąt całkowity tego układu jest stału
Siły bezwładności
Inercjalne i nieinercjalne układy odniesienia
- Inercjalne - układ odniesienia, w którym ciało nie poddane działaniu sił pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym nazywamy układem inercjalnym.
Każdy układ poruszający się względem układu inercjalnego ruchem jednostajnym i prostoliniowym jest też układem inercjalnym
- Nieinercjalny - układ odniesienia poruszający się ruchem niejednostajnym względem jakiegokolwiek inercjalnego układu odniesienia.
Przykłady sił bezwładności
- bezwładności - siła będąca wynikiem przyspieszenia układu. Siła nie jest oddziaływaniem z innymi ciałami, siła ta występuje tylko w nieinercjalnym układzie
- odśrodkowa - siła będąca wynikiem poruszania się po okręgu siła działająca na zewnątrz
![]()
- Siła coriolisa - działa na ciało poruszające się ruchem postępowym w obrajającym się układzie odniesienia.
![]()
Grawitacja
Prawo grawitacji- powszechnego ciążenia
- Dwa punkty materialne o masach m1 i m2 przyciągają się wzajemnie siła proporcjonalną do iloczynu ich mas i odwrotnie proporcjonalną do kwadratu ich odległości :
![]()
![]()
Ciężar ciał. Przyspieszenie ziemskie. Pole grawitacyjne
- Ciężar ciał - przyspieszenie ziemskie ciężarem ciała nazywamy siłę jaką ciało materialne jest przyciągane przez ziemię:
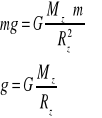
Wyznaczanie masy Ziemi : Dla Rz=6400 km g=9,81 m/s2 Mz=6 1024 kg
- Pole grawitacyjne - w przestrzeni otaczającej masę M powstaje pole grawitacyjne o takiej własności, że na masę próbną m umieszczoną w tym polu działa siła
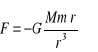
- Przyspieszenie ziemskie - przyspieszenie grawitacyjne ciał swobodnie spadających na Ziemię bez oporów ruchu.
Energia potencjalna pola grawitacyjnego
- 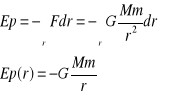
Potencjałem pola grawitacyjnego nazywamy stosunek energii potencjalnej masy próbnej m do wartości tej masy
![]()
Prędkości kosmiczne
- Pierwszą prędkością kosmiczną nazywamy najmniejszą możliwą prędkość jaką musi mieć punkt materialny swobodnie krążący wokół ziemi
Siła odśrodkowa 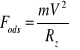
Siła grawitacji ![]()
WARUNKIEM STABILNOŚCI ORBITY JEST RÓWNOWAGA TYCH SIŁ !!
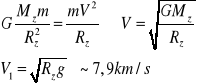
- Durgą prędkość kosmiczna nazywana prędkością ucieczki - nazywamy najmniejszą możliwą prędkością jaką musi mięc punkt materialny przy powierzchni Ziemi aby mogło oddalić się od niej w nieskończoność
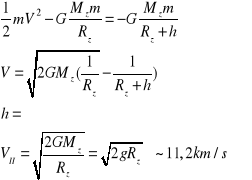
- Trzecią prędkość kosmiczna to prędkość potrzebna do opuszczenia układu słonecznego
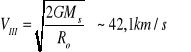
Ms - masa Słońca
Ro - Promień orbity Ziemi
Elementy szczególnej teorii względności
Postulaty Einsteina
- Zasada względności - zasada głosząca, że prawa fizyki są jednakowe we wszystkich układach inercjalnych - musi obowiązywać dla wszystkich praw zarówno mechaniki jak i elektrodynamiki
- Nieziemmność prędkości światła - prędkość światła w próżni jest taka sama dla wszystkich obserwatorów, taka sama we wszystkich kierunkach i nie zależy od prędkości źródła.
Pomiary prędkości światła
- Pierwszego dokonał Galileusz - Odsłanianie i przesłanianie latarni na oddalonych od siebie wzgórzach
- Ole Romer - 1676 - stwierdził, że światło potrzebuje mniej niż 1 s na przebycie 3000 mil francuskich ( około 13000 km ) - obliczenia na podstawie obserwacji Jowisza
- Armand Fizeau - 1849 - pomiar przy pomocy koła zębatego
- Albert Michelson - 1907 - INTERFERON
Doświadczenie Michelson'a-Morley'a
- MICHELSON-Do określenia prędkości wiatru eteru trzeba porównać prędkość światła w różnych kierunkach. W interferonie( urządzenie potrzebne do doświadczenia) wiązka światła zostaje podzielona półprzezroczystą płytką na dwie prostopadłe wiązki, które po odbiciu od zwierciadeł i powrotnym przejściu przez płytkę trafiają do teleskopu, w którym widać jasne i ciemne prążki jako wynik interferencji obu wiązek. Obraz interferencji zależy od różnicy czasu przebiegu obu wiązek między płytką, a zwierciadłem, bo w pozostałej części drogi światła obie wiązki biegną tą samą dragą.
MICHELSON - MOLEY - Długość drogi światła została zwiększona 10 - krotnie, układ interferonu pływał w korytach wypełnionych rtęcią by zapobiec jakimkolwiek drganiom jednak i to nie wykazało zmian w ich doświadczeniu.
Transformacja Lorentza
- Transformacja Lorentza - umożliwia obliczenie wielkości fizycznych w pewnym układzie odniesienia, jeśli znane są te wielkości w układzie poruszającym się względem pierwszego. Przekształceniu temu ulegają współrzędne czasoprzestrzeni, energia. Wzory zostały wprowadzone w oparciu o założenia, że prędkość światła jest stała i niezależna od prędkości układu.
Transformacja Lorentza - zachowuje odległości w czasoprzestrzeni, zachowany jest interwał, transformacje współrzędnych mają najprostszą postać
Czynnik Lorentza
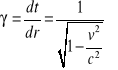
v - prędkość ciała względem danego układu
c - prędkość światła
v/c - prędkość wyrażona w stosunku do prędkości światła
Paradoks bliźniąt
-Na Ziemi( lub w dowolnym punkcie wszechświata przy założeniu, że z miejscem tym związany jest układ inercjalny) rodzą się bliźnięta, jeden z nich pozostaje na Ziemi, a drugi wysyłany szybkim statkiem kosmicznym w przestrzeń kosmiczną( im statek szybszy, tym spodziewamy efekt będzie większy), po pewnym czasie zawraca ląduje na ziemi i spotyka się ze swoim bratem bliźniakiem.
Zgodnie ze szczególną teorią względności czas w poruszającym się układzie odniesienie płynie wolniej ( dylatacja czasu ). Obserwacje bliźniaków przedstawiają się następująco :
Bliźniak pozostający na Ziemi spodziewa się, że skoro jego brat-kosmonatua poruszał się względem niego, to po powrocie brat- kosmonauta powinien być młodszy, jeżeli dylatacja czasu jest prawdą .
Bliźniak-kosmonauta myśli, że w jego układzie odniesienia to właśnie brat pozostały na Ziemi się poruszał względem niego
WNIOSEK :
Pierwsza odpowiedź prawidłowa - tylko jeden z nich może związać układ inercjalny, a skoro drugi zawraca rakietą to układ przestaje być już tym samym układem.
Masa i energia relatywistyczna
- masa relatywistyczna - jest wielkością względną jej wartość zależy od układu odniesienia, nie jest niezmiennikiem relatywistycznym. Może ona zmieniać się bez zmiany zachodzącej w samym obiekcie fizycznym, wyłącznie przez zmianę układu odniesienia.
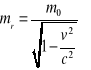
mr - masa relatywistyczna
m0 - masa spoczynkowa
v - prędkość ciała względem danego układu
Ruch drgający i falowy
-Ruchem drgającym( drganiem lub oscylacją) nazywamy ruch ciała zachodzący wokół stałego położenia równowagi rozróżniamy ruchy drgające :
- okresowe
- nie okresowe
Ruch okresowy PERIODYCZNY to taki ruch, w którym położenie ciała powtarza się w jednakowych odstępach czasu, zwanych okresami drgań T. Dla takiego ruchu położenie punktu materialnego spełnia następujący warunek
x(t)=x(t+T)
Dranie opisane funkcją![]()
nazywamy drganiem harmonicznym gdzie :
A - amplituda drgań
Drgania harmonicznie proste
Drgania złożone
- składanie drgań harmonicznych równoległych o tej samej częstotliwości :
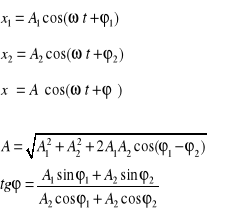
Twierdzenie Fouriera
- Dowolne drganie okresowe x(t) o okresie T jest superpozycją drgań harmonicznych i można je wyrazić szeregiem postaci
![]()
Ruch falowy. Rodzaje fal. Prędkości rozchodzenia się fal
- Ruch falowy - nazywamy przenoszenie się zaburzenia w ośrodku. Ruch falowy jest związany z transportem energii przez ośrodek.
- Rodzaje fal - fale Podłużne
- fale Poprzeczne
- fale harmoniczne
- impuls falowy
- fale płaskie
-fale kuliste
- Prędkośc rozchodzenia się fal
Podłużnej w ciele statycznym 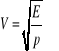
E - moduł Younga
p - gęstość ciała
Poprzecznej w ciele stałym 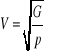
G - moduł sztywności
Podłużnej w cieczy 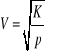
K- moduł ściśliwości ciecz
Podłużnej w gazie 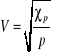
xp = cp/cv
p - ciśnienie gazu
Fala harmoniczna płaska. Równanie fali harmonicznej płaskiej
- Równanie fali harmonicznej płaskiej
![]()
Długościa fali ![]()
nazywamy odległośc dwóch punktów fali o fazach różniących się o 2![]()
![]()
![]()
![]()
![]()
Zasada Huygensa. Dyfrakcja fal.
- Zasada huygensa - Każdy punkt do którego dociera czoło fali staje się źródłem elementarnej fali kulistej.
- Dyferencja fali - jest obserwowana, gdy rozmiar obiektu, na którym zachodzi ugięcie jest porównywalny z długością fali.
Interferencja fal. Fale stojące.
- Interferencja - nakładanie się fal - zjawisko nakładania się fal o tych samych długościach, a więc tymch samych pulsacjach. W miejscu spotkania fal o przeciwnych fazach następuje wygłuszenie.
- Fala stojąca - powstaje w wyniki interferencji fal biegnących w przeciwnych kierunkach o jednakowej długości i amplitudzie. W - węzeł( miejsce nieruchomości) S- strzałka ( cząstki drgające z największą amplitudą.) położenie W i S nie ulega zmianie. Odległość między sąsiednimi strzałkami i węzami : ![]()
![]()
Powstaje wzdłuż struny drającej wewnątrz piszczałek organowych
Fale akustyczne. Źródła fal akustycznych. Dźwięki.Tony. Barwy.
- Podłużne fale mechaniczne mogące rozchodzić się w ciałach stałych, cieczach, gazach
Obejmują częstotliwość 20 Hz - 20 000 Hz
Fale o częstotliwościach <20 Hz - INFRADŹWIĘK
20 000 Hz - ULTRADŹWIĘK
Zjawisko Dopplera
- Zmiana odbieranej częstotliwości, gdy źródło i obserwator poruszają się względem siebie - źródło jest nieruchome, zbiżający się obserwator odbiera fale o większej częstotliwości
Źródło nieruchome
obserwator ruchomy ![]()
V0 - obserwator względem źródła
Źródło ruchome
Obserwator nieruchomy 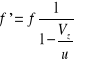
Vz - V źródła
Ultradźwięki i ich zastosowanie
- Fale dźwiękowe których częstotliwość jest zbyt wysoka aby słyszał je człowiek. Umowna granica ultradźwięków to 10 GHz
- Zastosowanie :
- lokacja ultra dźwiękowa
- defektoskopia
- koagulacja
- rozpad cząstek polimerów
- wytwarzanie emulsji, substancji trudno rozpuszczalnych
Mechanika cieczy i gazów
Prawo Pascala. Prawo Archimedesa. Pływanie ciał.
- Prawo Pascala - ciśnienie zewnętrzne wywierane na ciecz lub gaz jest przenoszone we wszystkich kierunkach jednakowo p = pp0 +'ro'gh
- Prawo Archimedesa - na ciało zanurzone w cieczy działa siła wyporu równa ciężarowi wypartej przez to ciało cieczy W='ro'cieczy*gV
- Pływanie ciał - na każde ciało działa siła wyporu i ciężkości Q = Vg*'ro', ich wypadkowa wyrażona jest związkiem: R= W-Q, gdy W>Q ciało pływa na powierzchni W = Q pływa w środku W<Q tonie
Przepływ cieczy i gazów. Równanie ciągłości. Prawo Bernouliego.
- Przepływ cieczy i gazów - ruch płynów nazywany przepływem. Uporządkowany ruch cząstek płynów poruszających się w jednym kierunku nazywamy STRUMIENIEM. Przepływ nazywamy LAMINARNYM gdy nie następuje mieszanie się sąsiednich warstw, TURBULENTNYM jeśli zachodzi mieszanie się poszczególnych warstw płynu.
- Równanie ciągłości v1/v2=s2/s1 prędkość cieczy w strumieniu są odwrotnie proporcjonalne do powierzchni przekrojów strumienia
- Prawo Bernouliego - suma energii kinetycznej, potencjalnej i ciśnienia jednostki masy ustalonego przepływu cieczy doskonałej jest wielkością stała
p + `ro'v^/2+'ro'gh = const
Przepływ cieczy rzeczywistych i gazów. Lepkość. Wzór Stokes'a. Siła Magnusa
- Lepkość - tarcie wewnętrzne procesy dążące do wyrównania prędkości
- Wzór Stokes'a F= 6pir'eta'v wyraża siłę tarcia wywartą przez ciecz na kulę o prędkośći v, promieniu r, `eta' współczynnik lepkości
- Siła Magnusa - powstaje zawsze wtedy gdy strumień opływający ciało będzie miał w płaszczyźnie prostopadłej do strumienia i przechodzącej przez to ciało, różne prędkości po przeciwległych stronach ciała.
Termodynamika
a)fenomenologiczna Mkroskopowe wiel charakt. Ukłąd:ciśnienie,temperatura,objętośc,energia,entropia
b) statyczna
mikroskopowe wiel. charakt. Cząski,atomy :prętkość, masa, energia pęd
Zerowa zasada temodynamiki:
Jeżeli ciało AiB są w równowadze termicznej z ciałem C to ciała A i B………nie wiem kurwa obcieło mi notatki
Pomiar temperatury:
Zmiana długości pręta
Opór elektryczny
Ciśnienie gazu
Kolor włókna żarówki
Temp termo dynam. - bezwzględna T
Jednostki kelwin
Punkt potrójny wody wynosi 273,16K
Kinetyczna teoria gazu
Zerowa zasada termodynamiki. Pomiar temperatury.
Kinetyczna teoria gazu doskonałego.
Równanie stanu gazu, równanie Clapeyrona.
dokonałego:
pV=nRT p V=NkT
n-liczba moli gazu
R=3,314L/mol
P=ciśnienie
V obj. T-temp
K=R/Na=1,38*10 do -23J/K -stała Boltmana
Na=6,023*10do23-l introgadra
Założenia:
A) cząsteczki gazu można traktować jako pkty mat.
B) znajdują się w szybkim ruchju
c)zderzają się sprężyście ze sobą
d) siły działają tylko w momencie zderzenia
e) V cząsteczek gazu jest zaniedbywalnie mała w porównaniu z objętością zajmowaną przez gaz
Założenia kinetycznej teorii gazu doskonałego
Ciśnienie gazu doskonałego
Kinetyczna interpretacja temperatury. Rozkład Maxwella. Ruchy Browna
Ciepło, praca i energia wewnętrzna
Pierwsza zasada termodynamiki
Praca sił ciśnienia
Ciepło przemiany
Ciepło
Energia wewnętrzna. Zasada ekwipartycji energii.
Silniki cieplne
Druga zasada termodynamiki
Gazy rzeczywiste. Równanie van der Vaalsa.
KINEMATYKA
Praca sił ciśnienia
Ciepło przemiany
Ciepło
Trzecia zasada ruchu obrotowego
Wyszukiwarka