WYDZIAŁ ELEKTRONKI TELEKOMUNIKACJI I INFORMATYKI KATEDRA METROLOGII I SYSTEMÓW ELEKTRONICZNYCH LABORATORIUM METROLOGII I TECHNIKI EKSPERYMENTU GRUPA 4A |
||
Ćwiczenie nr 1
Podstawowe mierniki i pomiary elektryczne
|
Imię i nazwisko |
Dariusz Kos |
|
Data wykonania ćwiczenia |
22.03.2005 |
|
Data odbioru sprawozdania |
4.04.2005 |
|
Ocena zaliczenia |
|
|
Uwagi i podpis
|
|
Sprawozdanie
6.4.2. Wzorcowanie woltomierza
Poniższa tabela zawiera wyniki wzorcowania woltomierza magnetoelektrycznego Vielfachmesser III na zakresie 2.5 V. Jako woltomierz wzorcowy użyty został multimetr cyfrowy Agilent 34401A.
Tablica 6.1
Ub [V] |
0.5 |
1.0 |
1.5 |
2.0 |
2.5 |
Uw [V] |
0.53880 |
1.05228 |
1.5631 |
2.0658 |
2.5549 |
ε [mV] |
38.80 |
52.28 |
63.1 |
65.8 |
54.9 |
δ [%] |
7.76 |
5.23 |
4.21 |
3.29 |
2.20 |
![]()
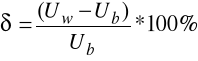
np. Ub = 0.5V, Uw = 0.53880V
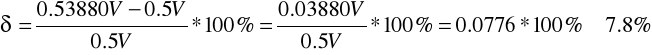
![]()
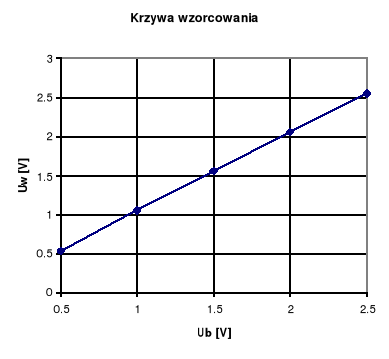
Zależność Uw(Ub) zbliżona jest do funkcji tożsamościowej, a niewielkie odchylenia wynikają z bezwzględnych błędów pomiarowych.
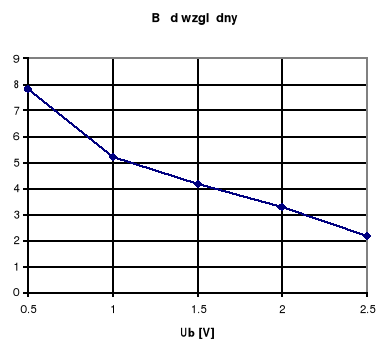
Z wykresu błędu względnego wynika, że im większą wartość napięcia mierzymy, tym mniejszy błąd pomiarowy zostaje popełniony. Wielkość tego błędu może być spowodowana niedokładnością przyrządów pomiarowych.
Sprawdzenie klasy woltomierza:
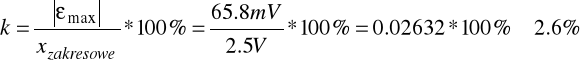
Wniosek: Woltomierz nie zachował swojej nominalnej klasy 1.5.
6.4.3. Pomiar rezystancji wewnętrznej woltomierza metodą podstawiania.
W zadaniu tym należało wyznaczyć rezystancję wewnętrzną woltomierza metodą, która polegała na podstawieniu rezystora dekadowego w miejsce woltomierza i ustawieniu rezystacji tego rezystora tak, by przepływał przez niego taki prąd, jaki płynął przez woltomierz. Rezystancja uzyskana na rezystorze dekadowym odpowiadała rezystancji wewnętrznej woltomierza.
Iw = 0.0512A, Rd = Rv = 50001.0Ω.
6.4.4. Zmiana zakresu pomiarowego woltomierza
W zadaniu tym należało dokonać wzorcowania woltomierza o dwukrotnie rozszerzonym zakresie pomiarowym. Do wyznaczenia rezystancji posobnika posłużyliśmy się poniższym wzorem:
![]()
gdzie:
n - mnożnik zakresu pomiarowego; w tym przypadku n = 2
Ra - rezystancja wewnętrzna woltomierza; z zad. 6.4.3 wiemy, że Ra = 50001.0Ω
stąd:
Rd = Rp = 50001.0Ω.
Tablica 6.2
Ub [V] |
1 |
2 |
3 |
4 |
5 |
Uw [V] |
1.08504 |
2.1135 |
3.1193 |
4.1208 |
5.1021 |
ε [mV] |
85.04 |
113.5 |
119.3 |
120.8 |
102.1 |
δ [%] |
8.50 |
5.68 |
3.98 |
3.02 |
2.04 |
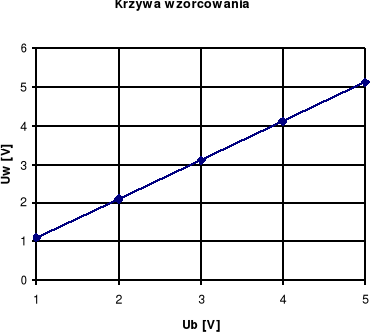
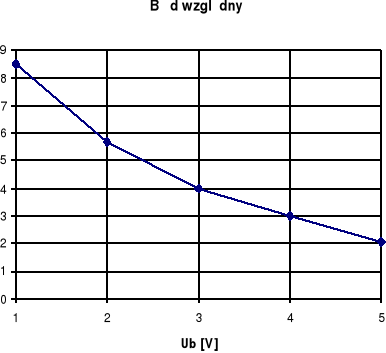
Zależność Uw(Ub) zbliżona jest do funkcji tożsamościowej, a niewielkie odchylenia wynikają z bezwzględnych błędów pomiarowych.
Wykres błędu względnego pokazuje, że tendencja malenia błędu względnego została zachowana, natomiast wartości tego błędu dla zakresu napięć 0V÷2.5V wzrosły prawie dwukrotnie.
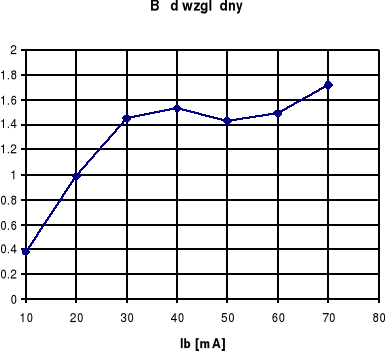
6.4.5. Pomiary miliamperomierzem magnetoelektrycznym
Poniższa tabela zawiera wyniki wzorcowania miliamperomierza magnetoelektrycznego:
Tablica 6.3
Ib [mA] |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
75 |
Iw [mA] |
10.0378 |
20.197 |
30.437 |
40.611 |
50.714 |
60.897 |
71.208 |
76.161 |
ε [μA] |
37.8 |
197 |
437 |
611 |
714 |
897 |
1208 |
1161 |
δ [%] |
0.38 |
0.98 |
1.46 |
1.53 |
1.43 |
1.50 |
1.73 |
1.55 |
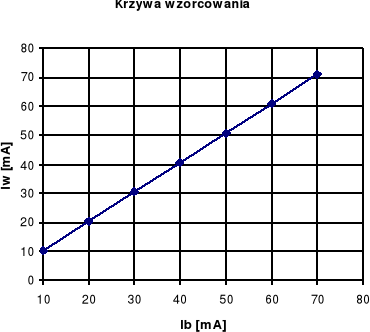
Zależność Uw(Ub) zbliżona jest do funkcji tożsamościowej, a niewielkie odchylenia wynikają z bezwzględnych błędów pomiarowych.
Wykres błędu względnego pokazuje, że wartości tego błędu oscylują w granicach 0.4%÷1.8%. Błędy pomiarowe mogą wynikać z niedokładności przyrządów pomiarowych.
Sprawdzenie klasy miliamperomierza:
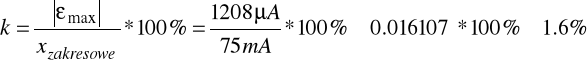
Wniosek: Miliamperomierz nie zachował swojej nominalnej klasy 0.5.
6.4.6.1. Pomiary napięcia z wykorzystaniem funkcji pamiętania wyniku oraz wartości maks. i min.
Um = 9.43V.
Tablica 6.4
Tryb pracy |
Opis zachowania multimetru |
|
1 |
normalny |
wyświetlanie bieżącej wartości napięcia |
2 |
pamiętania (D-H) |
pamiętanie bieżącej wartości napięcia - kolejne zmiany napięcia z zasilacza nie powodują już zmian wartości napięcia wyświetlanej przez multimetr |
3 |
pamiętania min. (MIN) |
pamiętanie najmniejszej wartości napięcia (7.52V) - kolejne zmiany napięcia z zasilacza powodują zmiany wartości napięcia wyświetlanej przez multimetr tylko wtedy, gdy napięcie z zasilacza jest niższe niż napięcie aktualnie wyświetlane przez multimetr |
4 |
pamiętania max. (MAX) |
pamiętanie największej wartości napięcia (11.28V) - kolejne zmiany napięcia z zasilacza powodują zmiany wartości napięcia wyświetlanej przez multimetr tylko wtedy, gdy napięcie z zasilacza jest wyższe niż napięcie aktualnie wyświetlane przez multimetr |
6.4.6.2. Pomiar rezystancji
Zadanie to polegało na zmierzeniu rezystancji 5 rezystorów za pomocą multimetru ME-21. Wyniki pomiarów zawiera poniższa tabela:
Tablica 6.5
Nr rezystora |
1 |
2 |
3 |
4 |
5 |
Ri [kΩ] |
7.36 |
7.42 |
7.37 |
7.36 |
7.43 |
Wyznaczenie średniej arytmetycznej rezystancji:
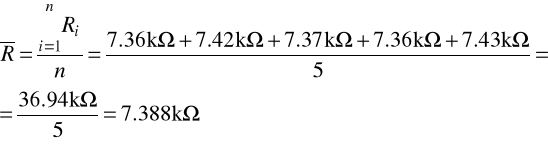
Wyznaczenie odchylenia standardowego pojedynczego pomiaru rezystancji:

Wyznaczenie odchylenia standardowego średniej arytmetycznej rezystancji:

Wszystkie wyniki są zgodne obliczeniami komputera.
6.4.7. Pomiary mocy
Zadanie to polegało na wyznaczeniu mocy wydzielanej na rezystorze RL = 100Ω i współczynnika przetwarzania mocy na częstotliowść układu AD7755.
Poniższe wzory posłużyły do wykonania odpowiednich obliczeń:
moc - 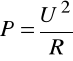
, współczynnik przetwarzania - 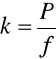
Tablica 6.6
U[V] |
0.5 |
1.00 |
1.5 |
2.0 |
2.5 |
3.0 |
3.5 |
4.0 |
f [kHz] |
0.050 |
0.200 |
0.451 |
0.801 |
1.253 |
1.805 |
2.454 |
3.21 |
P [mW] |
2.5 |
10 |
22.5 |
40 |
62.5 |
90 |
122.5 |
160 |
k [mW/kHz] |
50.000 |
50.000 |
49.889 |
49.938 |
49.880 |
49.861 |
49.919 |
49.844 |
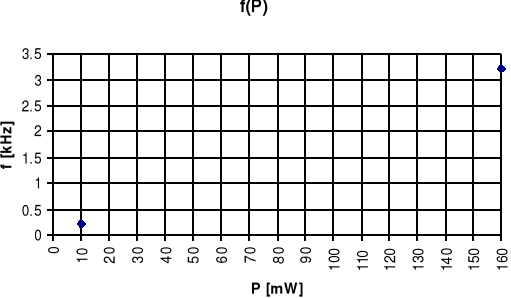
Charakterystyka f(P) jest liniowa, a jej niewielkie odchylenia spowodowane są błędami pomiarowymi, które wynikają z niedokładności przyrządów pomiarowych, niedokładnego określenia rezystancji badanego rezystora lub ewentualnych zakłóceń, które mogły dostać się do układu.
Uwaga:
Wartość współczynnika k odpowiada wartości częstotliwości sygnału generowanego przez generator.
6.4.9. Pomiary energii elektrycznej
W zadaniu tym pomiar energii elektrycznej zużywanej przez żarówkę odbywał się za pomocą układu laboratoryjnego składającego się m. in. z układu AD7755, multimetrów Agilent 34401A i Metex ME21 oraz komputera PC.
Pomiar odbywał się w czasie zadeklarowanym przez użytkownika. Komputer na bieżąco mierzył moc wydzielaną na żarówce i obliczał zużytą energię.
Obliczyliśmy teoretyczną wartość energii przy założeniu, że wartości napięcia i prądu żarówki nie zmieniają się w czasie:
E = U * I * t
dla napięcia 2V:
U = 2.002V, I = 27.0mA, t = 100s
E = 2.002V * 27.0mA * 100s = 54.054mW * 100s = 5405.4mWs =
≈ 1.502mWh
Wynik z komputera: 1.484mWh, ε = 0.018mWh
dla napięcia 4V:
U = 4.000V, I = 40.0mA, t = 100s
E = 4.000V * 40.0mA * 100s = 160mW * 100s = 16000mWs =
≈ 4.444mWh
Wynik z komputera: 4.414mWh, ε = 0.03mWh
Różnice między wartościami teoretycznymi i pomiarowymi świadczą o tym, że wartości napięcia i prądu żarówki ulegały zmianom w czasie.
6.5.7. Projekt uniwersalnego, wielozakresowego miernika elektrycznego.
Wyznaczenie oporu Rd:
Weźmy pod uwagę napięcie 200mV. Napięcie to odłoży się również na szeregowo połączone opory Rd, RA, przez które będzie płynął prąd IZ.
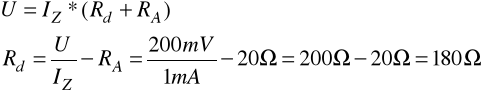
Wyznaczenie oporów Rw1, Rw2, Rw3 za pomocą równości odpowiednich napięć:
dla zakresu I1 = 50mA:
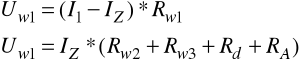
czyli 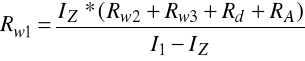
dla zakresu I2 = 10mA:
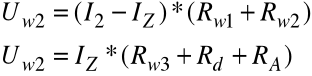
czyli 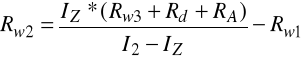
dla zakresu I3 = 2mA:
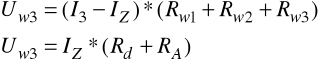
czyli 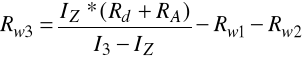
Po rozwiązaniu układu równań:
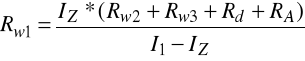
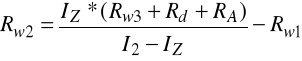
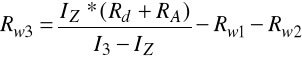
otrzymujemy następujące wyniki:
Rw1 = 8Ω, Rw2 = 32Ω, Rw3 = 160Ω
Wyznaczenie oporów Rw4, Rw5:
Z poprzednich obliczeń wiemy, że Rw1 + Rw2 + Rw3 = Rd + RA. Wynika z tego, że przez gałąź rezystorów Rw1, Rw2, Rw3 popłynie ten sam prąd, co przez gałąź oporów Rd i RA. Zatem przez gałąź rezystorów Rw4, Rw5 będzie płynął prąd 2*IZ. Napięcie, jakie odłoży się na rezystorze Rw4 przy zakresie U4 = 1V będzie równe:
![]()
zatem: 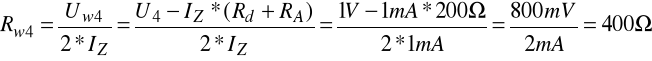
natomiast napięcie, jakie odłoży się na rezystorze Rw5 przy zakresie U5 = 5V będzie równe:
![]()
zatem: 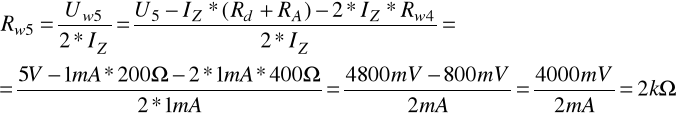
Strona 9
Wyszukiwarka