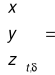Geodezja satelitarna |
UW MSC |
Ćwiczenie nr 1 |
|
|
Nr ew. 27 |
II ZGK 03 |
Data oddania: |
Prowadzący: mgr inż. Artur Oruba |
Zaliczenie: |
||
Na podstawie elementów orbity keplerowskiej wyznaczyć współrzędne horyzontalne satelity.
Dane:
G = 3
N = 27
M = N + 3 = 30
1. |
Duża półoś orbity - a |
20 251 000 m |
2. |
Mimośród orbity - e |
0.1500000 |
3. |
Argument perigeum - ω |
23Ⴐ 47' 30'' |
4. |
Rektascensja węzła wstępującego - |
15Ⴐ 37'10” |
5. |
Nachylenie orbity do równika - i |
55Ⴐ 00' 00” |
6. |
Moment przejścia przez pericentrum (CEST) - tp |
5h 30m 10s |
7. |
Moment na który wyznaczamy położenie satelity (UTC) - t0 |
30.09.2010 14h 27m 00s |
8. |
Współrzędne obserwatora - B, L |
B=51Ⴐ20'00” L=19Ⴐ30'00” |
Wyznaczenie współrzędnych horyzontalnych na podstawie elementów orbity
1. Obliczenia anomalii średniej.
M = n (to − tp)
![]()
= GM = 3,986004418 × 1014 m3 s-2
a = 20251000 m = 20251,000 × 103 m
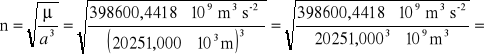
n = ![]()
![]()
![]()
t0 (UTC) = 14h 27m 00s
tp (CEST) = 5h 30m 10s
tp (UTC) = tp (CEST) - 2h = 5h 30m 10s - 2h = 3h 30m 10s
M = ![]()
![]()
× (14h 27m 00s - 3h 30m 10s) =
= ![]()
![]()
× 10h 56m 50s = ![]()
![]()
× 39410 s =
= 8,633872126 rad
2. Obliczenie anomalii mimośrodowej.
E = M + e × sin E
E0 = M
Ei+1 = M + e × sin Ei
M =8,633872126 rad
e = 0,1500000
E0 = M =8,633872126 rad
E1 =8,633872126 rad + 0,1500000 × sin 8,633872126 rad = 8,740520708 rad
E2 = 8,633872126 rad + 0,1500000 × sin 8,740520708 rad = 8,728686772 rad
E3 = 8,633872126 rad + 0,1500000 × sin 8,728686772 rad = 8,730055598 rad
E4 = 8,633872126 rad + 0,1500000 × sin 8,730055598 rad = 8,729897952 rad
E5 =8,633872126 rad + 0,1500000 × sin 8,729897952 rad = 8,729916117 rad
E6 =8,633872126 rad + 0,1500000 × sin 8,729916117 rad = 8,729914024 rad
E7 =8,633872126 rad + 0,1500000 × sin 8,729914024 rad = 8,729914265 rad
E8 =8,633872126 rad + 0,1500000 × sin 8,729914265 rad = 8,729914238 rad
E9 =8,633872126 rad + 0,1500000 × sin 8,729914238 rad = 8,729914241 rad
E10 =8,633872126 rad + 0,1500000 × sin 8,729914241 rad = 8,729914241 rad
E =8,729914241 rad
3. Obliczenie współrzędnych satelity w układzie orbitalnym.
x' = a (cos E - e)
y' = b sin E
z'= 0
E = 8,729914241 rad
e = 0,1500000
a = 20251000 m
![]()
x' = 20251000 m × (cos 8,729914241 rad - 0,1500000) =
= -18593272,7132987m ≈ -18593272,71 m
y' = 20021880,12 m × sin 8,729914241 rad = 12819624,7 m
z' = 0
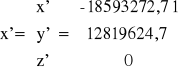
4. Transformacja współrzędnych orbitalnych do równikowych równonocnych (α, δ).
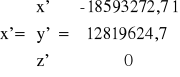
⇒ układ orbitalny
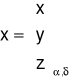
⇒ układ równikowy równonocny
![]()
= R3 (-) R1 (-i) R3 (-ω)![]()
= 15Ⴐ37'10”
cos = 0,9630712481
sin = 0,2692466732
i = 55Ⴐ 00' 00”
cos i = 0,5735764364
sin i = 0,8191520443
ω = 23Ⴐ 47' 30''
cos = 0,9150183515
sin = 0,4034122166
|
[B] |
[A] |
[A] × [B] |
|
|
|
|
1 |
0 |
0 |
|
|
|
|
|
0 |
0,573576436351 |
-0,8191520443 |
← |
|
|
|
|
0 |
0,8191520443 |
0,573576436351 |
R1(-i) |
|
0,963071248129 |
-0,26924667319 |
0 |
0,96307124813 |
-0,154433547311 |
0,220553962766 |
|
→ |
0,26924667319 |
0,963071248129 |
0 |
0,269246673196 |
0,552394974454 |
-0,7889017817 |
← |
R3(-) |
0 |
0 |
1 |
0 |
0,819152044289 |
0,573576436351 |
R3(-) ∙ R1(-i) |
|
|
|
|
|
|
|
|
|
|
|
|
0,91501835146 |
-0,4034122166 |
0 |
|
|
|
|
|
0,4034122166 |
0,91501835146 |
0 |
← |
|
|
|
|
0 |
0 |
1 |
R3(-ω) |
|
0,963071248129 |
-0,15443354731 |
0,220553962766 |
0,818927486161 |
-0,529824236817 |
0,220553962766 |
|
→ |
0,26924667319 |
0,552394974454 |
-0,78890178170 |
0,469208528123 |
0,396834141633 |
-0,78890178170 |
← |
R3(-) ∙ R1(-i) |
0 |
0,819152044289 |
0,573576436351 |
0,3304559419 |
0,749539153157 |
0,573576436351 |
R3(-) ∙ R1(-i) ∙ R3(-ω) |
|
|
|
|
|
|
|
|
|
|
|
|
-18593272,7133 |
← |
|
|
|
|
|
|
12819624,6799 |
|
|
|
|
|
|
|
0 |
|
|
|
|
0,818927486161 |
-0,52982423682 |
0,220553962766 |
-22018689,9449 |
|
|
|
→ |
0,469208528123 |
0,396834141633 |
-0,78890178170 |
-3636857,3669 |
R3(-) ∙ R1(-i) ∙ R3(-ω) ∙ |
|
|
R3(-) ∙ R1(-i) ∙ R3(-ω) |
0,3304559419 |
0,749539153157 |
0,573576436351 |
3464553,1786 |
← |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
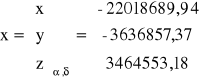
⇒ układ równikowy równonocny
![]()
(III ćw.)
α0 = 0,1636934497= 9Ⴐ 22' 44,2'' ≈ 9Ⴐ 22' 44''
α = 180Ⴐ + 9Ⴐ 22' 44'' = 189Ⴐ 22' 44''
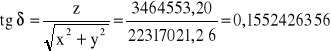
δ =0,1540132345= 8Ⴐ 49' 27,51'' ≈ 8Ⴐ 49' 28''
5. Zamiana rektascensji na kąt godzinny
t0 (UTC) ⇒UT1⇒...⇒GMST ⇒...⇒ Sv
t0 - moment, na który wyznaczamy położenie satelity (pkt. 7 danych),
Sv - prawdziwy czas gwiazdowy miejsca obserwacji (λ ≈ L)
t = Sv − α
t - kąt godzinny satelity w układzie równikowym godzinnym
14h 27m 00,s0000 UTC
- 0, 0800 poprawka (UT1 - UTC)IERS
14h 26m 59,s9200 UT1
+ 2m 22,s4258 redukcja UT1 na Sm
14h 29m 22,s3458 Δs interwał Sm odp. UT1
+ 0h 34m 32,s0898 GMST 0h UT1
15h 03m 54,s4356 GMST w zadanym momencie
+ 1h 18m 00,s0000 L
16h 21m 54,s4356 Sm obserwatora
+ 1, 0071 Eq
16h 21m 55,s4427 Sv
Obliczenie redukcji UT1 na Sm
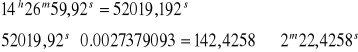
16h 21m 55,s4427 = 245Ⴐ 28' 51''
t = Sv − α = 16h 21m 55,s4427 - 189Ⴐ 22' 44'' =
= 245Ⴐ 28' 51' - 189Ⴐ 22' 44'' = 56Ⴐ 06' 07''
6. Transformacja układu równikowego godzinnego na układ horyzontalny
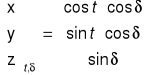
⇒ układ równikowy godzinny
t = 56Ⴐ 06' 07''
cos t = 0,557716941
sin t = 0,830031213
δ = 08Ⴐ 49' 28''
cos δ = 0,988163387
sin δ = 0,153405088
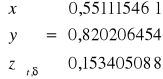
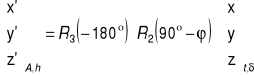
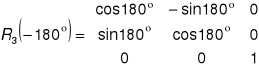
cos 180Ⴐ = -1
sin 180Ⴐ = 0
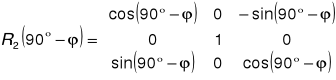
φ = 51Ⴐ 20' 00''
(90Ⴐ - φ) = 38Ⴐ 40' 00''
cos (90Ⴐ - φ) = 0,7807940267
sin (90Ⴐ - φ) = 0,6247885145
|
[B] |
[A] |
[A] × [B] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R2(90Ⴐ - φ) ↓ |
|
|
|
|
0,780794027 |
0 |
-0,624788515 |
|
|
|
0 |
1 |
0 |
|
|
|
0,624788515 |
0 |
0,780794027 |
-1 |
0 |
0 |
-0,780794027 |
0 |
-0,624788515 |
0 |
-1 |
0 |
0 |
-1 |
0 |
0 |
0 |
1 |
-0,624788515 |
0 |
0,780794027 |
R3(-180Ⴐ) ↑ |
|
|
|
R3(-180Ⴐ) ∙ R2( 90Ⴐ - φ) ↑ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-0,780794027 |
0 |
0,624788515 |
-0,334461923 |
|
|
0 |
-1 |
0 |
-0,820206454 |
R3(-180Ⴐ) ∙ R2(90Ⴐ - φ) ∙ |
|
0,624788515 |
0 |
0,780794027 |
0,464108386 |
← |
|
R3(-180Ⴐ) ∙ R2(90Ⴐ - φ) ↑ |
|
|
|
|
|
|
|
|
|
|
|
![]()
![]()
(III ćw.)
A0 = 67Ⴐ 48' 55,65'' ≈ 67Ⴐ 48' 56''
A = 67Ⴐ 48' 56''+180Ⴐ = 247Ⴐ 48' 56''
![]()
![]()
h = 27Ⴐ 39' 09,12'' ≈ 27Ⴐ 39' 09''
3
![]()
![]()
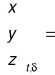
![]()
![]()
![]()
Wyszukiwarka