Nie sporządzając wykresu, napisz wzór funkcji, której wykres powstał po przesunięciu wykresu funkcji:
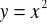
o 5 jednostek w dół,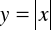
o 4 jednostki w lewo,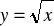
o 2 jednostki w prawo i 3 jednostki do góry,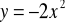
o 4 jednostki w lewo i 3 jednostki do dołu.
Podaj wzór funkcji f(x) powstałej po przesunięciu o wektor:
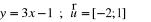
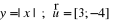
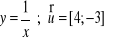
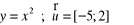
Wykres funkcji y=f(x) przekształcono w symetrii osiowej względem osi x. Napisz wzór otrzymanej funkcji.
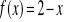
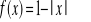
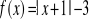
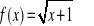
Jak należy przesunąć funkcję f(x)=|x|, aby otrzymać funkcję:
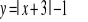
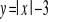
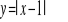
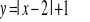
Narysuj wykres funkcji liniowej podanej wzorem y = 3x-1, a następnie podaj
miejsce zerowe tej funkcji,
argumenty, dla których funkcja przyjmuje wartości dodatnie,
argument, dla którego wartość funkcji wynosi 7,
miejsce przecięcia z osią y,
czy funkcja jest rosnąca czy malejąca.
Wyznaczyć dziedzinę funkcji:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
5) ![]()
6)![]()
7) ![]()
8) ![]()
9) ![]()
10) ![]()
Stosując odpowiednie przekształcenia narysuj wykres funkcji f(x), a następnie odczytaj zbiór wartości oraz monotoniczność tej funkcji, jeżeli:
Mając wykres funkcji f(x) sporządź wykresy następujących funkcji:
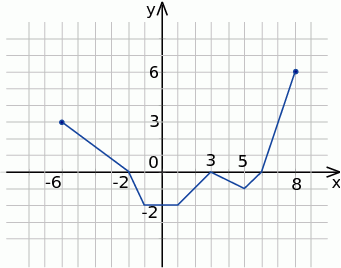
Odczytaj z wykresu funkcji f:dziedzinę i zbiór wartości
argumenty, dla których funkcja przyjmuje wartości nieujemne
argumenty, dla których funkcja przyjmuje wartości większe od 1
przedziały monotoniczności
odczytaj f(0), f(5), f(7)
wartość najmniejszą i największą
narysuj wykres funkcji g(x)=f(x)+2
narysuj wykres funkcji h(x)=f(x-2)
Funkcja liczbowa określona jest następująco:
Oblicz wartość funkcji f odpowiednio dla argumentów 2, -3, 3.
Sprawdź, która z liczb -3, 0, 2, 4 jest miejscem zerowym funkcji f.
Wyznacz te argumenty, dla których funkcja f przyjmuje wartość - 4.
Sporządź wykres funkcji f.
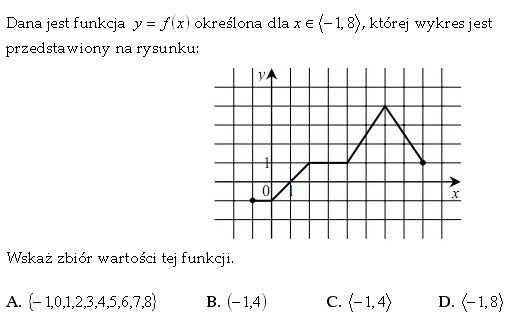
Dana jest funkcja f(x) określona dla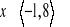
, której wykres przedstawiony jest na rysunku. Wskaż dziedzinę funkcji, zbiór wartości, monotoniczność, wartość najmniejszą i największą oraz przedziały, dla których funkcja przyjmuje wartości dodatnie i ujemne.Podaj wektor, o który została przesunięta funkcja f(x), tworząc funkcję g(x), jeżeli:
f(x)=|x| g(x)=|x+2|-4
f(x)=x2 g(x)=(x-3)2+1
f(x)=2x g(x)=2x+3-2
f(x)=
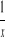
g(x)=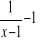
Wykres funkcji
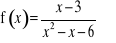
przesunięto o wektor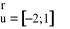
, a następnie przesunięty wykres odbito symetrycznie względem początku układu współrzędnych. Otrzymano wykres pewnej funkcji g. Znajdź wzór funkcji g i wyznacz dziedzinę.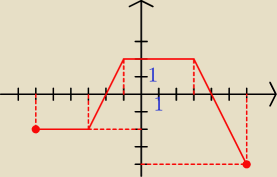
Obok zamieszczono wykres funkcji f. Funkcja g określona jest w następujący sposób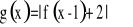
.Naszkicuj wykres funkcji g.
Podaj zbiór miejsc zerowych funkcji g.
Podaj zbiór rozwiązań nierówności
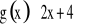
.Wykres funkcji y = -x + 2 przekształcono przez symetrie względem punktu (0, 0).
Napisz wzór funkcji, której wykres otrzymano.
Narysuj wykresy obu funkcji we wspólnym układzie współrzędnych.
Jak są położone względem siebie narysowane wykresy?
Korzystając z wykresu funkcji f(x) = x2, narysuj wykres funkcji g(x) = -x2 + 2. Oblicz współrzędne punktów wspólnych wykresów funkcji f oraz g.
Na rysunku przedstawione są wykresy funkcji y = f(x) oraz y = g(x).
Wykres funkcji g otrzymano przekształcając odpowiednio wykres funkcji f. Podaj, jakich przekształceń dokonano.
Narysuj wykres funkcji y = g(x).
Napisz wzór funkcji y = g(x).
a) |
b) |
c) |
d) |
e) |
f) |
g) |
h) |
i) |
j) |
|
|
oraz określ monotoniczność, zbiór wartości, wartość najmniejszą i największą (o ile istnieje) oraz miejsca zerowe.
a(x)=-f(x); b(x)=f(-x); c(x)=-f(-x); d(x)=f(x-3)-1; e(x)=2f(x); g(x)=f(2x); h(x)=f(|x|); i(x)=f(-|x|); j(x)=|f(x)|
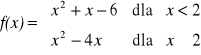
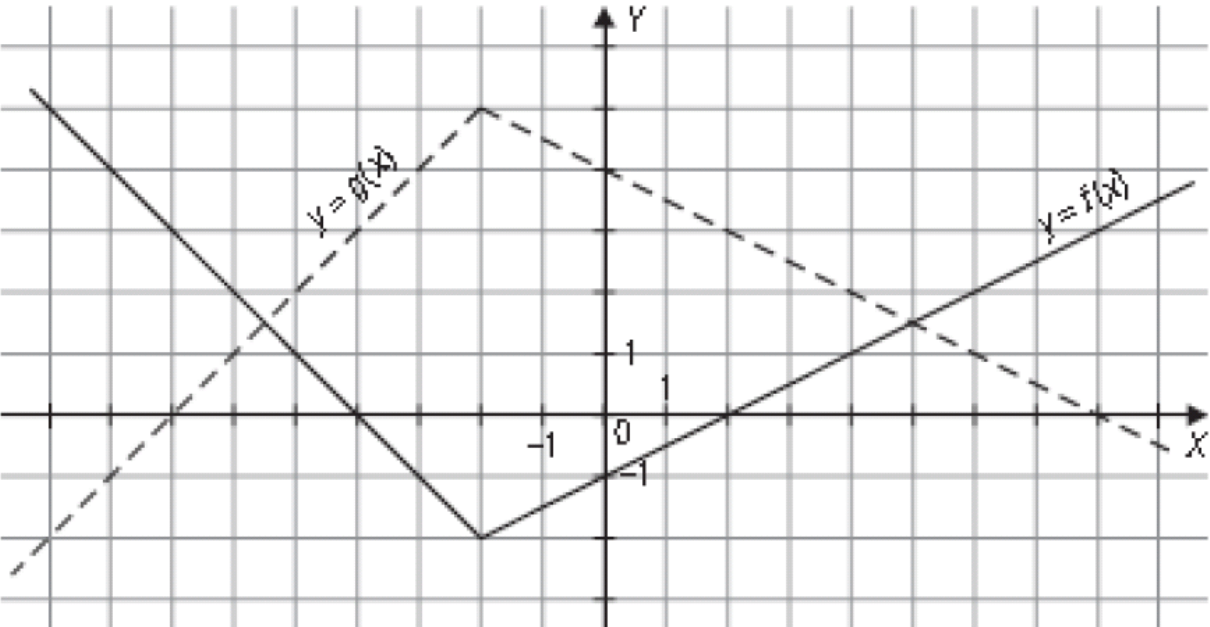
b) Który z podanych wzorów: g(x) = -f(x) + 3 czy g(x) = f(-x) + 3 jest poprawny?
18. Wykres funkcji f(x) = 2x przesunięto równolegle o wektor v = [-3, 1] i otrzymano wykres funkcji y = g(x).
Wyszukiwarka