Egzamin teoretyczny
Zadanie 1: Całkę![]()
obliczamy … (w jaki sposób?) i wynosi ona … (ile?).
Zadanie 2: Granica ![]()
nie istnieje ponieważ … (wyjaśnić).
Zadanie 3: Iloczyn pierwiastków zespolonych w równaniu z3-1=0 wynosi … (ile?).
Zadanie 4: Aby istniały rozwiązania niezerowe układu jednorodnego AX=0 i A(nxn) ..... (uzasadnić).
Zadanie 5: Reguły H nie można stosować do obliczenia granicy ![]()
![]()
ponieważ … (uzasadnić).
Zadanie 6: Funkcja F(x,y)= x3 + y3 + 9xy nie posiada ekstemum w punkcie (0,0) ponieważ .... (uzasadnić).
Zadanie 7: Całkę ![]()
obliczamy …. (w jaki sposób?) i wynosi ona …. (ile?).
Zadanie 8: Z definicji e:= .... (ile?) i granica ta istnieje ponieważ .... (wyjaśnić).
Zadanie 9: Funkcja pierwotna funkcji ![]()
jest postaci … (jakiej?).
Zadanie 10: Pierwiastki równania zespolonego f(z)=z4+z2+z2+1=0 są postaci … (obliczyć). Zaznaczyc je na wykresie w dziedzinie zespolonej.
Zadanie 11: Granica ![]()
wynosi … (ile?) i obliczamy ją … (w jaki sposób?).
Zadanie 12: Funkcja ![]()
nie ma ekstremów ponieważ … (uzasadnić).
Zadanie 13: Pole obszaru pomiędzy wykresami funkcji y=0 i ![]()
dla ![]()
wynosi … (uzasadnić).
Zadanie 14: Całkę ![]()
obliczamy … (w jaki sposób?) i wynosi ona … (ile?).
Zadanie 15: Całkę ![]()
obliczamy … (w jaki sposób?) i wynosi ona … (ile?).
Zadanie 16: Funkcja zadana wzorem 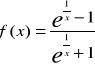
nie ma asymptoty pionowej ponieważ … (uzasadnić).
Zadanie 17: Warunkiem dostatecznym na to, żeby funkcja różniczkowalna w przedziale była rosnąca jest … (podać warunek). Wynika to z twierdzenia …. (jakiego?).
Zadanie 18: Całkę ![]()
obliczamy stosując twierdzenia … (jakie?). Wynik sprawdzamy następująco: … .
Zadanie 19: Bez wyliczeń stwierdzamy, że wyznacznik macierzy wynosi 0 jeśli … (podać 5 możliwości).
Zadanie 20: Dwie płaszczyzny A1x+B1y+C1z+D1=0, A2x+B2y+C2z+D2=0 nie przecinają się wzdłuż pewnej prostej wtedy i tylko wtedy gdy … (podać warunek równoważny na rząd macierzy utworzonej ze współczynników ich równań).
Zadanie 21: Liczba ![]()
jest jednym z pierwiastków stopnia trzeciego pewnej liczby zespolonej z. Pozostałe pierwiastki to: … (wyznaczyc i podać).
Zadanie 22: Całkę ![]()
obliczamy … (w jaki sposób?) i wynosi ona … (ile?).
Zadanie 23: Funkcja dana wzorem f(x)=|ln x2| ma minimum globalne w punkcie x=1 ponieważ … (uzasadnić).
Zadanie 24: Kąt między prostą 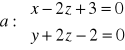
i płaszczyzną z=0 wynosi …(ile?) ponieważ … (uzasadnić).
Zadanie 25: Całkę ![]()
obliczamy … (w jaki sposób?) i wynosi ona … (ile?).
Zadanie 26: Punkt (0,0) jest punktem … (jakim?) dziedziny funkcji 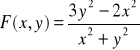
i granica ![]()
nie istnieje bo … (uzasadnić).
Zadanie 27: Całkę ![]()
obliczamy … (w jaki sposób?) i wynosi ona … (ile?).
Zadanie 28: Funkcja ![]()
osiąga ekstremum globalne w punkcie x=0 ponieważ na podstawie definicji … (uzasadnić).
Zadanie 29: Punkt (0,0) jest punktem skupienia Df funkcji 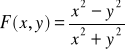
i granica ![]()
nie istnieje, bo … (uzasadnić).
Zadanie 30: Całkę ![]()
obliczamy … (w jaki sposób?) i wynosi ona … (ile?).
Zadanie 31: Warunkiem dostatecznym na to, żeby funkcja różniczkowalna była malejąca w przedziale jest … (podać warunek). Wynika to z tw. … (jakiego?).
Zadanie 32: Całkę 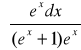
obliczamy … (w jaki sposób?) i wynosi ona … (ile?).
Zadanie 33: Całkę ![]()
obliczamy … (w jaki sposób?) i wynosi ona … (ile?).
Zadanie 34: Całkę ![]()
obliczamy … (w jaki sposób?) i wynosi ona … (ile?) a wynik sprawdzamy … (w jaki sposób?).
Zadanie 35: Całkę ![]()
obliczamy … (w jaki sposób?) i wynosi ona … (ile?).
Zadanie 36: Stosując twierdzenie … (jakie?) granica![]()
wynosi … (obliczyć).
Zadanie 37: Twierdzenia Rolle'a nie można stosować do funkcji ![]()
ponieważ … (uzasadnić).
Zadanie 38: Wyprowadzić wzór na odległośc między dwiema zadanymi prostymi równoległymi w przestrzeni.
Zadanie 39: Granica ![]()
nie istnieje ponieważ … (uzasadnić).
Zadanie 40: Przykładem funkcji ciągłej nieróżniczkowalnej w pewnym przedziale jest funkcja zadana wzorem f(x)=…. (podać funkcję). Uzasadnij dlaczego.
Zadanie 41: Prosta w R3 przechodząca przez punkty P1, P2 przecina się pod kątem prostym z prostą zawierającą punkty Q1, Q2 jeśli … (uzasadnić).
Zadanie 42: Funkcja g(x)=(x2+1)-1, ![]()
osiąga maksimum globalne w punkcie x=0 ponieważ na podstawie definicji … (uzasadnić).
Zadanie 43: Całkę ![]()
obliczamy przez podstawienie … (jakie?) i ostatecznie otrzymamy …. (ile?). Wynik sprawdzamy … (w jaki sposób?).
Zadanie 44: Macierz odwrotna do macierzy 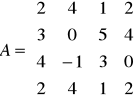
nie istnieje ponieważ … (uzasadnić).
Zadanie 45: Dwie płaszczyzny H1: x=y, H2:y+z=0 przecinają się wzdłuż prostej odległej od punktu (1,0,0) o … (obliczyć).
Zadanie 46: Całkę ![]()
obliczamy przez podstawienie … (jakie?). Ostatecznie otrzymamy … i wynik sprawdzamy … (w jaki sposób?).
Zadanie 47: Granica 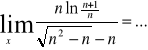
ponieważ… (uzasadnić podając odpowiednie twierdzenie).
Zadanie 48: Funkcja określona wzorem f(x,y)=xexy nie ma ekstremów ponieważ … (uzasadnić).
Zadanie 49: Całkę ![]()
obliczamy przez podstawienie … (jakie?) a następnie całkujemy funkcję wymierną. Ostatecznie otrzymamy … .
Zadanie 50: Układ 4 równań liniowych z 3 niewiadomymi jest sprzeczny, gdy rząd macierzy uzupełnionej rozszerzonej jest … (jaki?) co oznacza, że wyznacznik macierzy jest … (jaki?).
Zadanie 51: Prosta 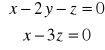
jest prostopadła do płaszczyzny Ax+By+Cz+D=0 wtedy i tylko wtedy, gdy … (podać warunek równoważny).
Zadanie 52: Granica ![]()
(ile?) ponieważ … (uzasadnić podając wykorzystane twierdzenie).
Zadanie 53: Całkę ![]()
obliczamy stosując twierdzenie … (jakie?).
Zadanie 54: Dlaczego nie można skorzystać z tw. H przy obliczaniu granicy ![]()
? Granica ta istnieje i wynosi … (ile?).
Zadanie 55: Funkcja odwrotna do f(x)=sinx, ![]()
nie istnieje ponieważ … (uzasadnić).
Zadanie 56: Równanie macierzowe AXA=A z zadaną macierzą niesobliwą A ma rozwiązanie X=… (obliczyć).
Zadanie 57: Funkcja ![]()
osiąga maksimum globalne w punkcie x=0 ponieważ … (uzasadnić na podstawie definicji).
Zadanie 58: Granica ![]()
wynosi … (ile?) ponieważ … (uzasadnić).
Zadanie 59: Dane są dwie macierze 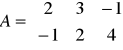
i ![]()
. Które z działań A*B, AT*B, A*BT są niewykonalne i dlaczego oraz ile wynosi wynik pozostałych?
Zadanie 60: Udowodnić, że ![]()
.
Zadanie 61: Prosta 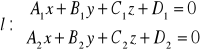
jest równoległa dp płaszczyzny OYZ wtedy i tylko wtedy, gdy … (podać warunek równoważny).
Zadanie 62: Na podstawie tw. … (jakiego?) granica ![]()
wynosi … (ile?).
Zadanie 63: Układ równań 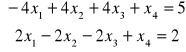
ma …. (ile?) rozwiązań na podstawie tw. … (jakiego?) ponieważ …. .
Zadanie 64: Układ równań 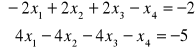
ma …. (ile?) rozwiązań na podstawie tw. … (jakiego?) ponieważ …. .
Zadanie 65: Całkę ![]()
obliczamy … (w jaki sposób?) i ostatecznie otrzymamy … .
Zadanie 66: Wykres funkcji o wartościach f(x)=x2+sinx nie posiada punktów przegięcia, ponieważ … (uzasadnić).
Zadanie 67: Układ 4 równań liniowych z 3 niewiadomymi może mieć rozwiązanie wtedy i tylko wtedy, gdy rząd macierzy uzupełnionej rozszerzonej spełnia nierówność … (jaką?) co oznacza, że wyznacznik macierzy wynosi … (ile?).
Zadanie 68: Prosta ![]()
należy do płaszczyzny Ax+By+Cz+D=0 ![]()
… (podać warunek równoważny).
Zadanie 69: Pierwiastki zespolone równania z3-8i=0 są wierzchołkami trójkąta. Podaj rysunek.
Zadanie 70: Jeśli Anxn jest macierzą nieosobliwą to równanie macierzowe AXA-1=A ma rozwiązanie A=…, ponieważ … .
Zadanie 71: Wzór Maclarina z drugą resztą Lagrange'a dla funkcji określonej wzorem f(x)=e-4x ma postać: … .
Zadanie 72: Funkcja ![]()
ma maksimum globalne w punkcie (0,0), ponieważ…. .
Zadanie 73: Pole zawarte między wykresami funkcji o wzorze y = arc ctg 2x i osią OX w przedziale <0; 0,5> wynosi …. .
Zadanie 74: Równanie 3 stopnia, które w dziedzinie zespolonej ma pierwiastki 2-2i, 2+2i, 2 jest postaci … .
Zadanie 75: Proste k: ![]()
i 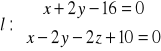
pokrywają się, ponieważ … .
Zadanie 76: 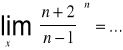
Zadanie 77: Funkcja F(x,y)=yexy^2 nie ma ekstremów ponieważ … .
Zadanie 78: Na podstawie definicji det[aij]4x4 jest sumą … (ilu?) iloczynów elementów z każdego wiersza i kolumny z odpowiednim znakiem. Wśród nich jest iloczyn a23, a14, a42, a31 ze znakiem … (jakim?), ponieważ … .
Zadanie 79: Na mocy twierdzenia … funkcja rzeczywista … wielu zmiennych rzeczywistych, określona na zbiorze … osiąga ekstrema absolutne.
Zadanie 80: Pierwiastki równania z3+1=0 to z1 i z2. Wówczas sześcian ich ilorazu wynosi … .
Zadanie 81: ![]()
Zadanie 82: ![]()
Zadanie 83: Pierwiastek równania xex=2 zawiera się w przedziale <0,1>. Wykazać i wyjaśnic na jakiej podstawie.
Zadanie 84: Obliczyć iloraz pierwiastków w równaniu z2-4z+5=0. Zaznaczyć w układzie współrzędnych.
Zadanie 85: Dana jest płaszczyzna 2x-y+4z+5=0. Punkty należące do tej płaszczyzny i odległe od osi OZ o 2/3 są postaci … .
Egzamin zadaniowy
Zadanie 1: Obliczyc punkty przegięcia i asymptoty funkcji e^((1-x)/x) ![]()
.
Zadanie 2: Wyznaczyć zbiór wartosci funkcji okreslonej wzorem 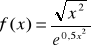
.
Zadanie 3: Wyznaczyc zbiór wartości funkcji okreslonej wzorem ![]()
.
Zadanie 4: Wyznaczyć asymptoty i ekstrema funkcji ![]()
.
Zadanie 5: Podać pełne badanie funkcji okreslonej wzorem ![]()
i naszkicować jej wykres.
Zadanie 6: Wyznaczyć ekstrema, punkty przegięcia i asymptoty funkcji ![]()
.
Zadanie 7:Wyznaczyć asymptoty i ekstrema funkcji ![]()
.
Zadanie 8: Podać pełne badanie funkcji okreś ![]()
.
Zadanie 9: Wyznaczyć ekstrema i punkty przegięcia funkcji ![]()
Zadanie 10: Podać pełne badanie funkcji funkcji ![]()
i naszkicowac jejwykres.
Zadanie 11: Wyznaczyć punkty przegięcia i asymptoty funkcji ![]()
.
Zadanie 12: Wyznaczyć punkty przegięcia i asymptoty funkcji ![]()
.
Zadanie 13: Wyznaczyć asymptoty i ekstrema funkcji 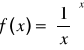
.
Zadanie 14: Zbadać przebieg funkcji zdefiniowanej jako ![]()
.
Zadanie 15: Zbadać wzajemne położenie płaszczyzn o równaniach: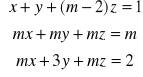
,![]()
w zależności od parametru ![]()
.
Zadanie 16: Dla jakich wartości parametru a prosta ![]()
jest równoległa do płaszczyzny H przechodzącej przez prostą 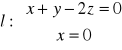
i punkt A=(3,1,0).
Zadanie 17: Zbadać wzajemne położenie prostych 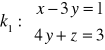
i ![]()
w zależności od parametru ![]()
. Jeśli leżą w jednej płaszczyźnie to napisać równanie tej płaszczyzny.
Zadanie 18: Pokazać, że proste 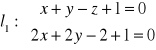
, 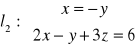
przecinają się. Znaleźć równanie prostej przechodzącej przez ich punkt przecięcia i prostopadłej do płaszczyzny zawierającej te proste.
Zadanie 19: Zbadać wzajemne położenie trzech płaszczyzn H1:2x-y+3z-1, H2:x+2y-z+3, H3:x+7y-6z+10=0. Jeśli przecinają się wzdłuż prostej to obliczyć odległość punktu (0,0,0) od tej prostej.
Zadanie 20: Pokazać, że proste 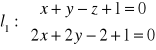
, 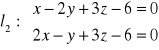
przecinają się. Znaleźć równanie prostej przechodzącej przez ich punkt przecięcia i prostopadłej do płaszczyzny zawierającej te proste.
Zadanie 21: Dany jest trójkąt o wierzchołkach A(-1,0,2), B(1,-2,5), C(3,0,-4). Znaleźć długość wysokości tego trójkąta z wierzchołka C oraz równanie prostej zawierającej tę wysokość.
Zadanie 22: Dany jest czworościan o wierzchołkach A(2,-1,3) B(1,-3,5) C(6,2,5) D(3,-2,-5). Znaleźć długość wysokości z wierzchołka D na podstawę ABC oraz równanie prostej zawierającej tę wysokośc.
8
Wyszukiwarka