Przebieg ćwiczenia:
Wyznaczenie częstotliwości sygnału pochodzącego od nieznanego generatora.
Odrysowanie z ekranu oscyloskopu obrazu 10 różnych krzywych Lissajous odpowiadających różnym częstotliwością sygnałów generatora.
Składanie drgań mechanicznych.
Zmierzenie czasu 10 pełnych okresów wahań jednego z wahadeł.
Rejestrowanie kolejnych krzywych Lissajous odpowiadających różnym różnicom faz drgań sprzężonych ze sobą wahadeł W1 oraz W2:
start W1 oraz W2 z maksymalnych wychyleń
start W1 z maksymalnego wychylenia, a W2 z pozycji odpowiadającej przeciwnemu maksymalnemu wychyleniu
start W1 z maksymalnego wychylenia, gdy W2 wcześniej wprawione w ruch przechodzi przez położenie równowagi
ustawienie masy M1 w połowie wahadła W1, a masę M2 na końcu wahadła W2. Wprawienie w ruch wahadeł z maksymalnych wychyleń.
Opracowanie wyników:
A. Wyznaczenie częstotliwości sygnału pochodzącego z nieznanego generatora.
1. Określenie liczby przecięć Nx z prostą równoległą do osi X oraz liczby przecięć Ny z prostą równoległą do osi Y dla każdej z 10 zarejestrowanych krzywych Lissajous.
Bierzemy pod uwagę tylko proste, które nie są styczne do krzywej i nei przechodzą przez punkty, w których krzywa Lissajous „przecina się”.
Nr krzywej Lissajous |
Vg [Hz] |
Nx |
Ny |
1 |
26 |
1 |
2 |
2 |
17,6 |
1 |
3 |
3 |
13,6 |
1 |
4 |
4 |
35,4 |
2 |
3 |
5 |
40 |
3 |
4 |
6 |
52,5 |
1 |
1 |
7 |
44,8 |
4 |
5 |
8 |
108 |
2 |
1 |
9 |
138 |
5 |
2 |
10 |
165 |
3 |
1 |
2. Wyznaczenie częstotliwości sygnału generowanego przez generator dla każdej z zarejestrowanych krzywych Lissajous.
Do obliczeń wykorzystujemy następujący wzór:
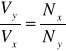
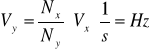
, gdzie:
Nx - liczba przecięć krzywej Lissajous z prostą równoległą do osi X
Ny - liczba przecięć krzywej Lissajous z prostą równoległą do osi Y
Vx = 50 [Hz] - częstotliwość napięcia sieciowego (częstotliwość drgań wzdłuż osi X)
Vy - częstotliwość drgań wzdłuż osi Y
Wyniki zawiera tabela:
Nr krzywej Lissajous |
Nx |
Ny |
Vx [Hz] |
Vy [Hz] |
1 |
1 |
2 |
50 |
25 |
2 |
1 |
3 |
50 |
16,7 |
3 |
1 |
4 |
50 |
12,5 |
4 |
2 |
3 |
50 |
33,3 |
5 |
3 |
4 |
50 |
37,5 |
6 |
1 |
1 |
50 |
50 |
7 |
4 |
5 |
50 |
40 |
8 |
2 |
1 |
50 |
100 |
9 |
5 |
2 |
50 |
125 |
10 |
3 |
1 |
50 |
150 |
Porównanie częstotliwości odczytanej z generatora z częstotliwością obliczoną z powyższych wzorów. Błąd bezwzględny liczymy ze wzoru:
![]()
gdzie:
Vg - częstotliwość odczytana z generatora
Vy - częstotliwość obliczona ze wzoru
Dla krzywej nr 1:
![]()
Dla następnych krzywych obliczenia wykonujemy analogicznie
Nr krzywej Lissajous |
Częstotliwość odczytana z generatora Vg [Hz] |
Częstotliwość obliczona ze wzoru Vy [Hz] |
Błąd bezwzględny [Hz] |
1 |
26 |
25 |
1 |
2 |
17,6 |
16,7 |
0,9 |
3 |
13,6 |
12,5 |
1,1 |
4 |
35,4 |
33,3 |
2,1 |
5 |
40 |
37,5 |
2,5 |
6 |
52,5 |
50 |
2,5 |
7 |
44,8 |
40 |
4,8 |
8 |
108 |
100 |
8 |
9 |
138 |
125 |
13 |
10 |
165 |
150 |
15 |
B. Składanie drgań mechanicznych:
1. Obliczenie okresu drgań oraz częstotliwości ruchu badanego wahadła:
a) Okres drgań T badanego wahadła:
![]()
gdzie:
t - czas 10 pełnych wahnięć badanego wahadła (16,6 ± 0,1) [s]
![]()
Niepewność wyznaczania okresu drgań T badanego wahadła:
![]()
![]()
Okres drgań badanego wahadła wynosi (1,66 ± 0,01) [s]
b) częstotliwość ruchu badanego wahadła ozn. przez v:
![]()
gdzie:
T - okres drgań badanego wahadła = 1,66 [s]
![]()
Niepewność wyznaczania częstotliwości ruchu badanego wahadła:
![]()
Częstotliwość ruchu badanego wahadła wynosi (0,6024 ± 0,0036) [Hz]
2. Wyznaczanie częstotliwości drgań, amplitudy drgań oraz wartości przesunięcia fazowego na podstawie analizy krzywych Lissajous.
2.1 Wyznaczanie częstotliwości drgań, amplitudy drgań oraz wartości przesunięcia fazowego dla krzywej nr 1
a) Wyznaczanie częstotliwości drgań składowych:
Częstotliwość drgań składowych wzdłuż osi X jest równa częstotliwości drgań badanego wahadła, które wykonywało drgania wzdłuż osi X, którą to częstotliwość obliczyliśmy wcześniej i wynosi ona:
vx = (0,6024 ± 0,0036) [Hz]
Po przekształceniu wzoru na stosunek częstotliwości drgań składowych otrzymujemy:
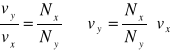
gdzie:
Nx - liczba przecięć krzywej Lissajous z prostą równoległą do osi X
Ny - liczba przecięć krzywej Lissajous z prostą równoległą do osi Y
vy - częstotliwość drgań wzdłuż osi Y
vx - częstotliwość drgań wzdłuż osi X - (0,6024 ± 0,0036) [Hz]
Po podstawieniu otrzymujemy:
![]()
Niepewność otrzymanej częstotliwości:
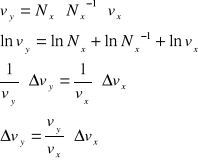
Po podstawieniu otrzymujemy:
![]()
Częstotliwości obu składanych drgań są jednakowe i wynoszą (0,6024 ± 0,0036) [Hz]
b) wyznaczanie amplitudy drgań składowych:
Amplitudy drgań składowych są równe połowie długości boków prostokąta, w którym mieści się otrzymana krzywa (amplituda drgań wzdłuż osi X jest równa połowie długości boku równoległego do osi X, a amplituda drgań wzdłuż osi Y jest równa połowie długości boku równoległego do osi Y)
![]()
długość boku
Zatem:
Długość boku x prostokąta, w którym mieści się otrzymana krzywa nr 1, który jest równoległy do osi X wynosi 0,034 [m]. Niepewność wyniku pojedynczego pomiaru długości boku x prostokąta, w którym mieści się otrzymana krzywa nr 1, który jest równoległy do osi X wynosi ![]()
![]()
![]()
Niepewność otrzymanej wartości amplitudy liczymy ze wzoru:
![]()
Amplituda drgań wzdłuż osi X wynosi (0,0170 ± 0,0005) [m]
Długość boku y prostokąta, w którym mieści się otrzymana krzywa nr 1, który jest równoległy do osi Y wynosi 0,018 [m]. Niepewność wyniku pojedynczego pomiaru długości boku y prostokąta, w którym mieści się otrzymana krzywa nr 1, który jest równoległy do osi Y wynosi ![]()
![]()
![]()
Niepewność otrzymanej wartości amplitudy liczymy ze wzoru:
![]()
Amplituda drgań wzdłuż osi Y wynosi (0,0090 ± 0,0005) [m]
c) wyznaczanie wartości przesunięcia fazowego dla krzywej nr 1:
Na podstawie wiadomości zamieszczonych w skrypcie uczelnianym, z którego korzystaliśmy oraz porównując otrzymaną krzywą z ilustracjami widać, że przesunięcie fazowe otrzymanej krzywej Lissajous (powstałej ze złożenia drgań o tej samej częstotliwości) powinno wynosić ![]()
.
Licząc przesunięcie fazowe według wzoru otrzymujemy:
![]()
gdzie:
a = (0,010 ± 0,001) [m]
b = (0,018 ± 0,001) [m]
zatem:
![]()
Przesunięcie fazowe dla krzywej nr 1 wynosi ![]()
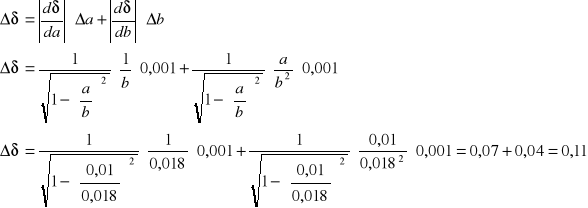
Przesunięcie fazowe dla krzywej nr 1 wynosi ![]()
2.2 Wyznaczanie częstotliwości drgań, amplitudy drgań oraz wartości przesunięcia fazowego dla krzywej nr 2
a) Wyznaczanie częstotliwości drgań składowych:
Częstotliwość drgań składowych wzdłuż osi X jest równa częstotliwości drgań badanego wahadła, które wykonywało drgania wzdłuż osi X, którą to częstotliwość obliczyliśmy wcześniej i wynosi ona:
vx = (0,6024 ± 0,0036) [Hz]
Po przekształceniu wzoru na stosunek częstotliwości drgań składowych otrzymujemy:
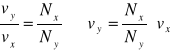
gdzie:
Nx - liczba przecięć krzywej Lissajous z prostą równoległą do osi X
Ny - liczba przecięć krzywej Lissajous z prostą równoległą do osi Y
vy - częstotliwość drgań wzdłuż osi Y
vx - częstotliwość drgań wzdłuż osi X - (0,6024 ± 0,0036) [Hz]
Po podstawieniu otrzymujemy:
![]()
Niepewność otrzymanej częstotliwości:
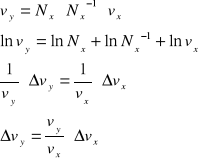
Po podstawieniu otrzymujemy:
![]()
Częstotliwości obu składanych drgań są jednakowe i wynoszą (0,6024 ± 0,0036) [Hz]
b) wyznaczanie amplitudy drgań składowych:
Amplitudy drgań składowych są równe połowie długości boków prostokąta, w którym mieści się otrzymana krzywa (amplituda drgań wzdłuż osi X jest równa połowie długości boku równoległego do osi X, a amplituda drgań wzdłuż osi Y jest równa połowie długości boku równoległego do osi Y)
![]()
długość boku
Zatem:
Długość boku x prostokąta, w którym mieści się otrzymana krzywa nr 1, który jest równoległy do osi X wynosi 0,058 [m]. Niepewność wyniku pojedynczego pomiaru długości boku x prostokąta, w którym mieści się otrzymana krzywa nr 1, który jest równoległy do osi X wynosi ![]()
![]()
![]()
Niepewność otrzymanej wartości amplitudy liczymy ze wzoru:
![]()
Amplituda drgań wzdłuż osi X wynosi (0,0290 ± 0,0005) [m]
Długość boku y prostokąta, w którym mieści się otrzymana krzywa nr 1, który jest równoległy do osi Y wynosi 0,033 [m]. Niepewność wyniku pojedynczego pomiaru długości boku y prostokąta, w którym mieści się otrzymana krzywa nr 1, który jest równoległy do osi Y wynosi ![]()
![]()
![]()
Niepewność otrzymanej wartości amplitudy liczymy ze wzoru:
![]()
Amplituda drgań wzdłuż osi Y wynosi (0,0165 ± 0,0005) [m]
c) wyznaczanie wartości przesunięcia fazowego dla krzywej nr 1:
Na podstawie wiadomości zamieszczonych w skrypcie uczelnianym, z którego korzystaliśmy oraz porównując otrzymaną krzywą z ilustracjami widać, że przesunięcie fazowe otrzymanej krzywej Lissajous (powstałej ze złożenia drgań o tej samej częstotliwości) powinno wynosić ![]()
.
Licząc przesunięcie fazowe według wzoru otrzymujemy:
![]()
gdzie:
a = (0,028 ± 0,001) [m]
b = (0,033 ± 0,001) [m]
zatem:
![]()
Przesunięcie fazowe dla krzywej nr 1 wynosi ![]()
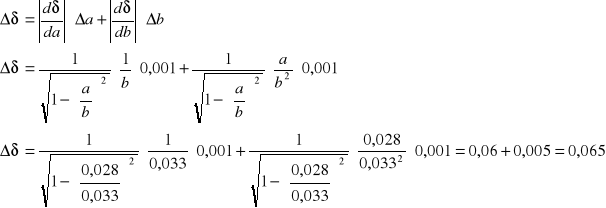
Przesunięcie fazowe dla krzywej nr 2 wynosi ![]()
Wyznaczenie częstotliwości drgań i amplitudy drgań dla krzywej nr 4.
a) Wyznaczanie częstotliwości drgań składowych:
Częstotliwość drgań składowych wzdłuż osi X jest równa częstotliwości drgań badanego wahadła, które wykonywało drgania wzdłuż osi X, którą to częstotliwość obliczyliśmy wcześniej i wynosi ona:
vx = (0,6024 ± 0,0036) [Hz]
Po przekształceniu wzoru na stosunek częstotliwości drgań składowych otrzymujemy:
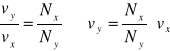
gdzie:
Nx - liczba przecięć krzywej Lissajous z prostą równoległą do osi X równą 5
Ny - liczba przecięć krzywej Lissajous z prostą równoległą do osi Y równą 8
vy - częstotliwość drgań wzdłuż osi Y
vx - częstotliwość drgań wzdłuż osi X - (0,6024 ± 0,0036) [Hz]
Po podstawieniu otrzymujemy:
![]()
Niepewność otrzymanej częstotliwości:
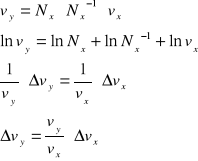
Po podstawieniu otrzymujemy:
![]()
Częstotliwości obu składanych drgań nie są jednakowe i wynoszą
Vx = (0,6024 ± 0,0036) [Hz]
Vy = (0,3765 ± 0,0023) [Hz]
b) wyznaczanie amplitudy drgań składowych:
Amplitudy drgań składowych są równe połowie długości boków prostokąta, w którym mieści się otrzymana krzywa (amplituda drgań wzdłuż osi X jest równa połowie długości boku równoległego do osi X, a amplituda drgań wzdłuż osi Y jest równa połowie długości boku równoległego do osi Y)
![]()
długość boku
Zatem:
Długość boku x prostokąta, w którym mieści się otrzymana krzywa nr 1, który jest równoległy do osi X wynosi 0,039 [m]. Niepewność wyniku pojedynczego pomiaru długości boku x prostokąta, w którym mieści się otrzymana krzywa nr 1, który jest równoległy do osi X wynosi ![]()
![]()
![]()
Niepewność otrzymanej wartości amplitudy liczymy ze wzoru:
![]()
Amplituda drgań wzdłuż osi X wynosi (0,0195 ± 0,0005) [m]
Długość boku y prostokąta, w którym mieści się otrzymana krzywa nr 1, który jest równoległy do osi Y wynosi 0,05 [m]. Niepewność wyniku pojedynczego pomiaru długości boku y prostokąta, w którym mieści się otrzymana krzywa nr 1, który jest równoległy do osi Y wynosi ![]()
![]()
![]()
Niepewność otrzymanej wartości amplitudy liczymy ze wzoru:
![]()
Amplituda drgań wzdłuż osi Y wynosi (0,0250 ± 0,0005) [m]
Zestawienie wyników:
Wyznaczone częstotliwości sygnału generowanego przez generator dla każdej z zarejestrowanych krzywych Lissajous i porównanie ich z odczytanymi z generatora:
Nr krzywej Lissajous |
Częstotliwość odczytana z generatora Vg [Hz] |
Częstotliwość obliczona ze wzoru Vy [Hz] |
Błąd bezwzględny [Hz] |
1 |
26 |
25 |
1 |
2 |
17,6 |
16,7 |
0,9 |
3 |
13,6 |
12,5 |
1,1 |
4 |
35,4 |
33,3 |
2,1 |
5 |
40 |
37,5 |
2,5 |
6 |
52,5 |
50 |
2,5 |
7 |
44,8 |
40 |
4,8 |
8 |
108 |
100 |
8 |
9 |
138 |
125 |
13 |
10 |
165 |
150 |
15 |
Składanie drgań mechanicznych - wyniki:
- Okres drgań badanego wahadła wynosi (1,66 ± 0,01) [s]
- Częstotliwość ruchu badanego wahadła wynosi v = (0,6024 ± 0,0036) [Hz]
Dla krzywej nr 1:
- Częstotliwość obu składanych drgań dla krzywej (0,6024 ± 0,0036) [Hz]
- Amplituda drgań wzdłuż osi X wynosi (0,0170 ± 0,0005) [m]
- Amplituda drgań wzdłuż osi Y wynosi (0,0090 ± 0,0005) [m]
- Przesunięcie fazowe dla krzywej nr 1 wynosi ![]()
Dla krzywej nr 2:
- Częstotliwość obu składanych drgań dla krzywej (0,6024 ± 0,0036) [Hz]
- Amplituda drgań wzdłuż osi X wynosi (0,0290 ± 0,0005) [m]
- Amplituda drgań wzdłuż osi Y wynosi (0,0165 ± 0,0005) [m]
- Przesunięcie fazowe dla krzywej nr 2 wynosi ![]()
Dla krzywej nr 4:
- Częstotliwości obu składanych drgań nie są jednakowe i wynoszą
Vx = (0,6024 ± 0,0036) [Hz] ; Vy = (0,3765 ± 0,0023) [Hz]
- Amplituda drgań wzdłuż osi X wynosi (0,0195 ± 0,0005) [m]
- Amplituda drgań wzdłuż osi Y wynosi (0,0250 ± 0,0005) [m]
Wnioski:
1. Metoda wyznaczania częstotliwości nieznanego sygnału na podstawie krzywych Lissajous uzyskiwanych na ekranie oscyloskopu jest średnio dokładna, ponieważ trudno jest znaleźć idealną częstotliwość dla danej krzywej.
2. Powstałe krzywe Lissajous podczas składania drgań mechanicznych z użyciem dwóch sprzężonych ze sobą wahadeł również nie są dokładnie, ponieważ trudno jest wprawić obydwa wahadła jednocześnie w ruch z identycznych wychyleń, a co za tym idzie powstała krzywa jest bardzo niedokładna.
![]()
![]()
Wyszukiwarka