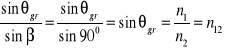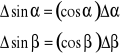Ćwiczenie nr 29

Wyznaczanie współczynnika załamania światła

1. Cel ćwiczenia

Wyznaczanie współczynnika załamania światła na granicy dwóch ośrodków.

Wyznaczanie kąta granicznego.

2. Wprowadzenie

W ośrodkach jednorodnych światło rozchodzi się po liniach prostych. W optyce geometrycznej strumień światła, pochodzący od źródła punktowego, przedstawiamy umownie w postaci promienia świetlnego, którego bieg jest odwracalny. Podstawowymi prawami optyki geometrycznej są prawa odbicia i załamania światła zachodzące na granicy dwóch ośrodków.

Prawo odbicia.

Kątem padania nazywamy kąt, który tworzy promień padający z prostą prostopadłą (normalną) do granicy dwóch ośrodków, a kąt odbicia to kąt, jaki tworzy promień odbity z normalną do powierzchni. Kąt odbicia jest równy kątowi padania, a promień padający, promień odbity i normalna leżą w jednej płaszczyźnie.

Prawo załamania (prawo Snella).

Światło przechodzące z jednego ośrodka do drugiego zmienia kierunek rozchodzenia się. Jeżeli α oznacza kąt padania, β kąt załamania oba mierzone do normalnej do powierzchni to stosunek sinusa kąta padania α do sinusa kąta załamania β jest dla dwóch danych ośrodków wielkością stałą, równą stosunkowi prędkości światła w tych dwóch ośrodkach v₁/v₂ i nazywa się współczynnikiem załamania ośrodka drugiego względem pierwszego n₂₁.:

(29.1)

Współczynnik n₂₁ nazywamy względnym współczynnikiem załamania. Jeżeli światło pada z próżni gdzie ma prędkość c do ośrodka, w którym rozchodzi się z prędkością v to bezwzględny współczynnik załamania światła n w tym ośrodku definiujemy wzorem:

(29.2)

Dlatego względne współczynniki załamania światła można wyrazić przez bezwzględne współczynniki załamania tych ośrodków. Dla ośrodka pierwszego otrzymujemy:

(29.3)

dla ośrodka drugiego:

(29.4)

Względny współczynnik załamania można zapisać w postaci:

(29.5)

Ze względu na odwracalność biegu promieni świetlnych:

(29.6)

W podręcznikach i tablicach podawane bezwzględne wartości współczynników załamania, które przyjmują wartości od n=2,42 dla diamentu do n=1 dla próżni. Współczynniki załamania światła zależą też od długości fali, co nazywamy dyspersją.

Jeżeli światło przechodzi z ośrodka, w którym rozchodzi się z dużą prędkością do ośrodka, w którym biegnie wolniej, to kąt załamania jest mniejszy od kąta padania (rysunek29.1).

Rys. 29.1. Załamanie promienia świetlnego na granicy dwóch ośrodków
(powietrze-badany materiał)

W przeciwnym przypadku kąt załamania jest większy od kąta padania. W ośrodku gdzie światło rozchodzi się wolniej, dla dużych kątów padania, na granicy dwóch ośrodków (np. woda-powietrze) następuje tylko odbicie i światło nie przechodzi do drugiego ośrodka. Zjawisko to nosi nazwę całkowitego wewnętrznego odbicia. Kąt padania α_gr ,dla którego kąt załamania β = 90⁰ nazywamy kątem granicznym (rysunek 29.2)

Rys. 29.2. Kąt graniczny

Prawo odbicia można wtedy zapisać w postaci:

(29.7)

Jeżeli drugim ośrodkiem jest powietrze to :

(29.8)

Zjawisko całkowitego wewnętrznego odbicia znalazło wiele zastosowań miedzy innymi w światłowodach i endoskopach.

3. Opis stanowiska laboratoryjnego

Punktowe źródło światła np. laser, stolik optyczny ze skalą stopniową, półokrągłe przezroczyste krążki ze szkła lub tworzyw sztucznych.

4. Program ćwiczenia

1. Sprawdzić czy promień światła przechodzi przez środek stolika optycznego.

2. Umieścić badaną półokrągłą płytkę na środku stolika optycznego tak, aby światło padało na płaską część prostopadle do niej.

3. Ustawić kąt padania α na około 5⁰ i na skali kątomierza odczytać kąt załamania β.

4. Zwiększać kąt padania α , co 5⁰ i odczytywać kąt załamania β.

5. Wyniki pomiarów zanotować w tabeli 291. Wyznaczyć niepewności pomiarowe szerokości wiązki światła padającej i załamanej. Wyniki zapisać w mierze kątowej Δα, Δβ.

6. Odwrócić badaną płytkę o 180⁰ w stosunku do pierwotnego położenia. Tym razem światło będzie padało na powierzchnię kolistą.

7. Sprawdzić dla kąta padania α=0⁰ czy promień światła przechodzi przez środek stolika optycznego.

8. Ustawić kąt padania α na około 4⁰ i na skali kątomierza odczytać kąt załamania β.

9. Zwiększać kąt padania α, co 4⁰ i odczytywać kąt załamania β.

10. Wyznaczyć wartość kąta granicznego α_gr. Pomiar tego kąta powtórzyć 10 razy.

11. Wyniki pomiarów zanotować w tabeli 29.2. Wyznaczyć niepewności pomiarowe szerokości wiązki światła padającej i załamanej. Wyniki zapisać w mierze kątowej Δα, Δβ.

Tabela 29.1.

Δα= Δβ=

1p.	α	β	sinα	sinβ	n21	Δn21/ n21 %

gdzie:

(29.9)

Δα, Δβ, - określić w mierze łukowej kąta

Tabela 29.2.

Δα= Δβ= Δα_gr=

1p.	α	β	sinα	sinβ	n12		Δn12/ n12 %		n21=1/ n12

gdzie

(29.10)

Δα,Δβ, - określić w mierze łukowej kąta

5. Sprawozdanie

1. Obliczyć względne współczynniki załamania n₂₁i n₁₂.

2. Obliczyć względne niepewności systematyczne pomiaru n₂₁ i n₁₂ metodą różniczki zupełnej ze wzoru 29.9

(29.11)

3. niepewności pomiaru kątów Δα, Δβ wyrażone w kątach należy zamienić na miarę łukową kąta w radianach.

4. Sporządzić wykresy zależności sinusa kąta podania sinα od sinusa kąta załamania sinβ dla obu pomiarów. Nanieść na wykres niepewności pomiarowe

Δsinα i Δsinβ wyliczone metodą różniczki zupełnej ze wzoru:

	(29.12)
		(29.13)

niepewności pomiaru kątów Δα, Δβ wyrażone w kątach należy zamienić na miarę łukową kąta w radianach.

5. Narysować proste przechodząca przez prostokąty niepewności pomiarowych.

6. Wyznaczyć współczynniki kierunkowe prostych i zapisać wartości względnych współczynników załamania.

7. Z pomiarów kąta granicznego wyznaczyć średnią arytmetyczną α_{gr śr}. Obliczyć wartość współczynnika załamania i jego odwrotność. Obliczyć odchylenia standardowe średniej arytmetycznej. Sprawdzić, jakie niepewności dominują: systematyczne czy statystyczne.

8. Dyskusja wyników i niepewności pomiarowych.

6. Pytania kontrolne

1. Światło i jego właściwości

2. Widmo fal elektromagnetycznych

3. Zjawiska falowe

4. Optyka geometryczna i granice jej zastosowania

182

---