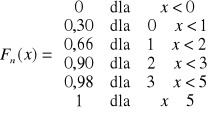ZADANIA
(na podstawie: J.Podgórski - Statystyka dla studiów licencjackich. PWE 2005, wyd. drugie)
Rozdział 2
1. Liczba podręczników zakupionych na początku roku akademickiego przez studentów w grupie liczącej 20 osób była następująca:
3 2 3 0 4 6 4 6 1 5 0 3 5 4 0 3 4 5 4 2.
Określ zbiorowość w tym przykładzie, liczbę jej elementów i badaną cechę. Przedstaw powyższe dane w postaci szeregu rozdzielczego (empirycznego rozkładu cechy). Przedstaw rozkład graficznie.
2. Liczba niewykorzystanych pokoi w pewnym hotelu sieci Astor w
kolejnych dniach kwietnia była następująca:
13 |
38 |
7 |
10 |
14 |
26 |
19 |
8 |
11 |
5 |
12 |
20 |
25 |
44 |
10 |
0 |
26 |
18 |
5 |
22 |
16 |
4 |
7 |
17 |
28 |
33 |
7 |
11 |
8 |
14 |
Co jest tu elementem zbiorowości, co badaną cechą? Przedstaw powyższe dane w postaci szeregu z klasami o jednakowej rozpiętości równej 10. Zapisz w tablicy środki przedziałów. Narysuj histogram oraz wielobok liczebności tego rozkładu.
3. Rozkład liczby błędów drukarskich na 50 stronach składu był następujący:
Liczba błędów |
Liczba stron |
0 |
15 |
1 |
18 |
2 |
12 |
3 |
4 |
5 |
1 |
Wyznacz skumulowany rozkład liczebności (częstości) i przedstaw go graficznie. Zapisz dystrybuantę empiryczną i sporządź jej wykres.
4. Wśród kupujących samochody przeprowadzono ankietę na temat pewnego nowego rozwiązania technicznego. Zbadano ogółem 50 osób, spośród których 22 opowiedziały się za wprowadzeniem rozwiązania, 15 było przeciwnych, a pozostali nie mieli zdania. Przedstaw te dane w postaci szeregu rozdzielczego. Przedstaw te dane graficznie za pomocą diagramu i wykresu kołowego. Czy jest możliwe zdefiniowanie dystrybuanty tej cechy?
5. Waga (w kg) 20 poborowych, którzy stanęli w pewnym dniu przed komisją poborową była następująca: 76, 67, 80, 73, 69, 73, 64, 85, 77, 74, 76, 76, 58, 63, 74, 69, 81, 74, 71, 83.
Utwórz szereg rozdzielczy z klasami prawostronnie domkniętymi o jednakowej rozpiętości równej 5 kg i dolnej granicy pierwszego przedziału równej 55 kg. Przedstaw ten rozkład graficznie za pomocą histogramu i wieloboku liczebności. Utwórz skumulowany szereg rozdzielczy i przedstaw go w postaci ogiwy (wieloboku liczebności skumulowanych).
7. Rozkład czasu obsługi klientów (w sek.) przy kasie stacji benzynowej jest następujący:
Czas obsługi |
Liczba przypadków |
0 - 10 |
4 |
10 - 20 |
15 |
20 - 30 |
10 |
30 - 40 |
7 |
40 - 50 |
2 |
50 - 60 |
0 |
60 - 70 |
2 |
Sporządź wykres dystrybuanty empirycznej czasu obsługi. Zaznacz na nim częstość przypadków, w których obsługa trwała mniej niż 30 sek. Wskaż także przybliżoną wartość czasu obsługi, poniżej której obsługiwanych było 20% klientów.
9. Zbudowano rozkład płac tak, aby w każdym przedziale było 20% jednostek (wartości cechy 2 , 5, 10, 20 będziemy nazywać kwintylami, jako że dzielą zbiorowość na 5 równych części).
Przedziały |
Częstości |
0-2 |
0,2 |
2-5 |
0,2 |
5-10 |
0,2 |
10-20 |
0,2 |
20-50 |
0,2 |
Czy narysowanie histogramu w zwykły sposób, tzn. z częstościami na osi rzędnych da właściwy obraz rozkładu? Narysować histogram tak, by pola prostokątów równe były częstości jednostek w odpowiednich klasach (należy odmierzać na osi rzędnych wartości wi/hi).
10. Poniżej dany jest rozkład wyników skoku w dal uczniów 5 klas pewnej Szkoły Podstawowej:
Wyniki (w cm) |
Chłopcy |
Dziewczęta |
80-90 |
1 |
9 |
90-100 |
5 |
14 |
100-110 |
7 |
8 |
110-120 |
12 |
4 |
120-130 |
6 |
1 |
130-140 |
3 |
- |
Naszkicuj, na jednym wykresie, wielobok liczebności wyników dla chłopców i dziewcząt. W której grupie wyniki są: a) na ogół lepsze, b) bardziej zróżnicowane?
11. Rozkład wyników dla ogółu uczniów Szkoły Podstawowej utworzony na podstawie danych z zadania 10 jest następujący:
Wyniki (w cm) |
Chłopcy i dziewczęta |
80-90 |
10 |
90-100 |
19 |
100-110 |
15 |
110-120 |
16 |
120-130 |
7 |
130-140 |
3 |
Naszkicuj ten rozkład i omów jego własności. W jaki sposób wynikają one z własności łączonych rozkładów? Omawiany rozkład określamy jako niejednorodny. Czy analiza jego własności jest wartościowa?
12. Podaj własne przykłady cech, których rozkład może być:
a) symetryczny, b) prawostronnie asymetryczny, c) lewostronnie asymetryczny.
Rozdział 3
1. Premie wypłacone pracownikom w związku z wykonaniem pewnego zadania były następujące: 200, 500, 500, 800, 1000. Oblicz łączną i średnią arytmetyczną wypłaconych premii. Sprawdź na tym przykładzie następujące własności średniej arytmetycznej: a) ![]()
, b)![]()
.
2. Dzienne zużycie energii elektrycznej (w kWh) przez lokatorów pewnego budynku było następujące:
15, 12, 10, 5, 10, 18, 6, 13, 41, 25.
Oblicz na podstawie tego zbioru danych średnią arytmetyczną, medianę i dominantę. Przedstaw dane na osi liczbowej w postaci kropek, zaznacz na niej obliczone miary i wypowiedz się czy poszczególne miary dobrze reprezentują tendencję centralną zbioru.
3. Oblicz na podstawie danych z zadania 1 rozstęp, wariancję i odchylenie standardowe.
4. Oblicz na podstawie danych zadania 2 wariancję i odchylenie standardowe. Dla skrajnych wartości zbioru, czyli dla 5 i 41, oblicz wartości standaryzowane. Czy wskazują one na to, że wartości te są nietypowe? Przyjmij, że wartość jest nietypowa, gdy odchyla się od średniej o więcej niż trzy odchylenia standardowe, tzn. gdy bezwzględna wartość standaryzowana jest większa od 3.
5. Notowania trzech akcji (A, B i C) w ciągu jednego tygodnia były następujące:
A: |
6,30 |
6,55 |
5,00 |
5,60 |
5,65 |
B: |
52,5 |
56,0 |
55,0 |
54,5 |
55,5 |
C: |
102 |
106 |
110 |
108 |
104 |
Jeśli ryzyko gracza giełdowego mierzyć zróżnicowaniem kursów, to jak należy uszeregować akcje pod względem rosnącego ryzyka na podstawie:
rozstępu kursów, b) odchylenia standardowego, c) współczynników zmienności?
6. W zakładzie doświadczalnym obserwowano po ilu dniach wykiełkują ziarna pewnej rośliny, otrzymując:
Liczba dni |
4 |
5 |
6 |
7 |
8 |
9 |
Liczba ziaren |
15 |
16 |
10 |
5 |
3 |
1 |
Oblicz w tym rozkładzie średnią, medianę i dominantę.
7. Rozkład absencji pracowników pewnej firmy był następujący:
Liczba dni nieobecności |
0 |
1 |
2 |
3 |
4 |
6 |
10 |
14 |
Liczba pracowników |
40 |
5 |
2 |
20 |
10 |
7 |
5 |
1 |
Oblicz dominantę i średnią w powyższym rozkładzie. Wypowiedz się, czy miary te reprezentują dobrze - w omawianym przypadku - tendencję centralną.
8. Dwudziestu palaczy zapytano o liczbę paczek papierosów wypalanych tygodniowo. Uzyskano następujące odpowiedzi: 2 7 3 6 5 3 4 5 5 6 4 4 5 6 4 4 5 5 6 7.
a) przedstaw te dane w postaci szeregu rozdzielczego, b) oblicz kwartyl drugi i trzeci c) ile wynosi wartość dystrybuanty empirycznej dla x = 3?
9. W firmie Z-K pracuje 10 pracowników administracyjno - biurowych, 17 pracowników nadzoru technicznego i 23 pracowników bezpośrednio produkcyjnych. Średnie miesięczne wynagrodzenie pracownika administracyjno - biurowego wynosi 1600 zł, średnie wynagrodzenie pracownika nadzoru technicznego wynosi 1500 zł, natomiast pracownika bezpośrednio produkcyjnego - 1050 zł. Oblicz średnią płacę ogółu pracowników.
10. Dzienny przebieg taksówek w pewnym mieście charakteryzuje szereg rozdzielczy:
Przebieg w km |
0-40 |
40-80 |
80-120 |
120-160 |
160-200 |
Liczba taksówek |
26 |
82 |
56 |
28 |
8 |
Oblicz miary tendencji centralnej (średnią arytmetyczną, medianę i dominantę). Obliczenie dominanty zilustruj graficznie.
11. Na podstawie danych zad. 10 obliczyć wariancję i odchylenie standardowe dziennego przebiegu taksówek.
12. Na podstawie poniższych danych o wydatkach grupy emerytów na książki i czasopisma (w zł) oblicz medianę i średnią arytmetyczną tych wydatków:
Wydatki w zł |
5-10 |
10-15 |
15-20 |
20-25 |
25-30 |
Liczba osób |
4 |
10 |
8 |
6 |
1 |
13. Na podstawie danych zad. 10 oblicz kwartyle pierwszy i trzeci, rozstęp międzykwartylowy i odchylenie ćwiartkowe. Obliczenie kwartyli zilustruj na wykresie dystrybuanty.
14. Zarejestrowano liczbę widzów na 10 poniedziałkowych seansach filmu "Nie lubię poniedziałku" otrzymując: 10, 16, 4, 15, 6, 12, 22, 31, 8, 20. Oblicz na podstawie tego zbioru danych (bez uprzedniego grupowania) klasyczne miary zróżnicowania i asymetrii.
15. Dla 15 pracowników zatrudnionych w dziale marketingu zanotowano następujące ilości delegacji służbowych w ciągu ostatniego roku: 8, 6, 0, 13, 20, 9, 8, 6, 7, 14, 2, 3, 6, 5, 10. Dla cechy "liczba wyjazdów służbowych" oblicz: 1)średnią, 2)medianę, 3)dominantę. Zinterpretuj wszystkie wyniki. Czy na podstawie tych miar można określić kierunek asymetrii?
16. Rozkład opłat za naprawy samochodów wykonane w ciągu miesiąca w pewnym warsztacie, ustalony na podstawie 120 obserwacji był następujący:
Opłaty w zł |
Liczba napraw |
0-100 |
20 |
100-200 |
42 |
200-300 |
22 |
300-400 |
20 |
400-500 |
16 |
Sporządź wielobok liczebności rozkładu opłat i oceń jego asymetrię za pomocą: a) współczynnika skośności, b) współczynnika asymetrii.
17. Zbadano zużycie wody w pewnej zbiorowości rodzin uzyskując wyniki:
Zużycie wody w l. |
30-50 |
50-70 |
70-100 |
100-150 |
150-250 |
Odsetek rodzin |
15 |
30 |
25 |
20 |
15 |
Oceń asymetrię rozkładu zużycia wody przy pomocy pozycyjnego miernika asymetrii. Przyjmując ![]()
oraz ![]()
naszkicuj wykres pudełkowy. Który element wykresu wskazuje na asymetrię rozkładu?
19. W badaniu gospodarstw domowych otrzymano następujące charakterystyki rozkładu dochodów i oszczędności (obie cechy w tys. zł):
Kategoria |
Średnia arytmetyczna |
Dominanta |
Wariancja |
Dochód |
12 |
10 |
9 |
oszczędności |
8 |
9 |
16 |
Porównaj zróżnicowanie i asymetrię rozkładu obu kategorii.
20.Poddano analizie opisowej dane o wieku grupy 25 osób otrzymując następujący zestaw miar opisowych:
Średnia 35 |
Wariancja 121,0 |
Mediana 33 |
Dominanta 28 |
Minimalna wartość 21 |
Maksymalna wartość 63 |
Kwartyl pierwszy 26 |
Kwartyl trzeci 43 |
Oceń zróżnicowanie i asymetrię rozkładu wieku.
23. Zbadano powierzchnię (w ha) 120 plantacji tytoniu znajdujących się na terenie pewnego powiatu otrzymując rozkład:
Powierzchnia w ha |
0,5-3,5 |
3,5-6,5 |
6,5-9,5 |
9,5-12,5 |
Liczba plantacji |
33 |
59 |
27 |
5 |
Oceń koncentrację upraw tytoniu w tym powiecie.
24. W badaniu koncentracji płac pracowników pewnej gałęzi przemysłu stwierdzono, że płace trzeciej części pracowników o najniższych zarobkach stanowiły 20% całkowitego funduszu płac, zaś płace trzeciej części pracowników o najwyższych zarobkach stanowiły 50% całkowitego funduszu płac. Sporządź wykres krzywej koncentracji Lorenza oraz oblicz wartość współczynnika koncentracji.
25. Rozkład dochodów ludności USA w 1964 r. był następujący:
Procentowe grupy ludności według malejącego dochodu |
Odsetek ogólnego dochodu |
górne 10% |
30 |
drugie 10% |
15 |
trzecie 10% |
13 |
czwarte 10% |
11 |
piąte 10% |
9 |
szóste 10% |
8 |
siódme 10% |
6 |
ósme 10% |
4 |
dziewiąte 10% |
3 |
dolne 10% |
1 |
Nakreśl krzywą Lorenza i oblicz współczynnik Giniego.
Odpowiedzi do zadań
Uwaga: Wariancje i momenty centralne 3-go rzędu w poniższych rozwiązaniach obliczono z użyciem dzielników n-1, a więc odpowiedzi w tym zakresie będą nieznacznie się różnić od tych, uzyskanych przy użyciu dzielnika n (konsekwentnie, niewielkie różnice występować będą także dla odchyleń standardowych, klasycznych współczynników zmienności i asymetrii).
Rozdział 2
Zbiorowość - grupa studentów, liczebność zbiorowości - 20, cecha - liczba książek zakupionych przez studenta
Element zbiorowości - jeden dzień kwietnia, cecha - liczba niewykorzystanych pokoi.
x - liczba błędów drukarskich na stronie
x - waga poborowych w kg
brak
x - czas obsługi
brak
Nie. Przyjąć za wysokości słupków
:a) w grupie chłopców , b) w grupie chłopców
Rozkład jest nieregularny (bimodalny) co wynika z połączenia rozkładów o różnych wartościach dominujących. Analiza takiego rozkładu nie jest wartościowa.
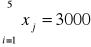
,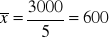
a)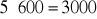
b)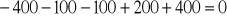
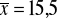
kWh,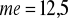
kWh,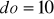
kWh.
Średnia arytmetyczna ze względu na wystąpienie w zbiorze nietypowej dużej wartości (41) nie reprezentuje zbyt dobrze tendencji centralnej, z kolei dominanta jest tu dość przypadkową wielkością.Rozstęp = 800 zł,
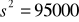
(zł)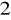
,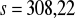
zł.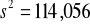
,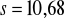
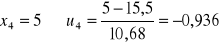
;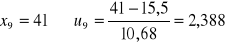
W świetle sformułowanego w zadaniu kryterium wartości 5 i 41 nie są izolowane.Uszeregowanie akcji według rosnących wartości miar zróżnicowania
X - liczba dni po których kiełkuje ziarno;
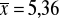
;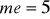
;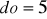
X - liczba dni nieobecności;
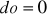
,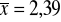
. Żadna z tych miar nie reprezentuje dobrze tendencji centralnej w tym rozkładziea)
x - miesięczne wynagrodzenie w zł.
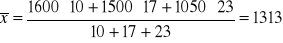
zł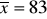
km,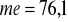
km,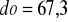
km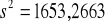
(km)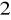
;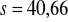
km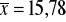
,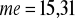
zł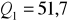
km ,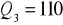
km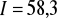
km ,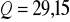
kmX - liczba widzów na seansie ;
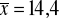
;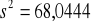
;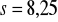
;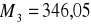
;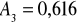
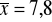
;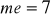
;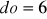
. Określenie kierunku asymetrii na podstawie relacji obliczonych miar byłoby trudne, bowiem rozkład empiryczny jest nieregularny.Jest:
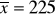
;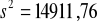
;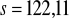
;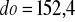
;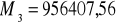
skąd
a)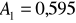
b)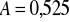
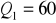
;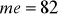
;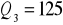
;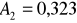
; kierunek asymetrii określa relacja długości odcinków reprezentujących różnice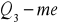
i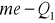
.brak
Dochód
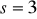
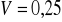
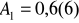
Oszczędności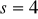
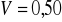
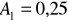
Rozstęp = 42 ;
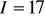
;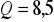
;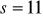
;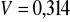
;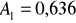
;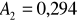
brak
brak
Liczba książek |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
liczba studentów |
3 |
1 |
2 |
4 |
5 |
3 |
2 |
Liczba niewykorzystanych pokoi |
Liczba dni |
Środki przedziałów |
0-9 |
9 |
4,5 |
10-19 |
12 |
14,5 |
20-29 |
6 |
24,5 |
30-39 |
2 |
34,5 |
40-49 |
1 |
44,5 |
|
|
|
0 |
15 |
0,30 |
1 |
33 |
0,66 |
2 |
45 |
0,90 |
3 |
49 |
0,98 |
5 |
50 |
1,00 |
Opinia o nowym rozwiązaniu |
Liczba zbadanych |
Za |
22 |
Przeciwko |
15 |
Brak opinii |
13 |
Podział koła według opinii: za - 158,4o, przeciwko - 108o, brak - 93,6o. Dystrybuanty nie można zdefiniować, bowiem cecha jest niemierzalna.
|
55-60 |
60-65 |
65-70 |
70-75 |
75-80 |
80-85 |
|
1 |
2 |
3 |
6 |
5 |
3 |
|
1 |
3 |
6 |
12 |
17 |
20 |
|
10 |
20 |
30 |
40 |
50 |
60 |
70 |
|
0,1 |
0,475 |
0,725 |
0,9 |
0,95 |
0,95 |
1 |
Fn(30)=0,725; Fn(x)=0,2 dla x![]()
12
i |
1 |
2 |
3 |
4 |
5 |
|
0,04 |
0,10 |
0,05 |
0,04 |
0,02 |
Rozdział 3
a) A, B, C; b) A, B, C; c) B, C, A
Kryterium c wydaje się najlepsze.
|
|
|
|
2 |
1 |
0,05 |
0,5 |
3 |
2 |
0,10 |
0,15 |
4 |
5 |
0,25 |
0,40 |
5 |
6 |
0,30 |
0,70 |
6 |
4 |
0,20 |
0,90 |
7 |
2 |
0,10 |
1,00 |
![]()
, ![]()
, ![]()
|
0,266 |
0,742 |
0,960 |
1,000 |
|
0,104 |
0,571 |
0,913 |
1,000 |
|
|
|
1 |
|
0,2 |
0,5 |
1 |
|
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
0,01 |
0,04 |
0,08 |
0,14 |
0,22 |
0,31 |
0,42 |
0,55 |
0,70 |
1,0 |
K = 0,406
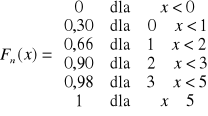
K = 0,251
K = 0,2
Wyszukiwarka